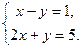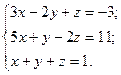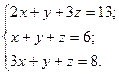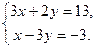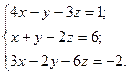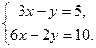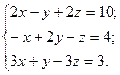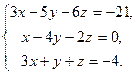Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Омельченко В.П., Курбатова Э.В. Математика. - Ростов-на-Дону: «Феникс», 2011.- с. 340 – 360.Содержание книги
Поиск на нашем сайте
3. Спирина М.С., Спирин П.А. Теория вероятности и математическая статистика. – М.: Издательский центр «Академия». -2007г. – с.182-190.
Практическое занятие № 15 Решение систем линейных алгебраических уравнений по формулам Крамера и матричным методом Цели: в результате выполнения практической работы, обучающиеся должны уметь решать системы линейных алгебраических уравнений по формулам Крамера и матричным методом. Пояснения к работе Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида
где числа
Такую систему принято записывать в компактной матричной форме А∙Х=В. А - матрица коэффициентов системы, называемая основной матрицей: А = В = Произведение матриц А∙Х определено, т. к. в матрице А столбцов столько же, сколько строк в матрице Х (n штук). Решением системы называется n значений неизвестных Пусть дана система n линейных уравнений с n неизвестными
или в матричной форме А∙Х=В. Основная матрица такой системы квадратная. Определитель Найдем решение данной системы в случае Умножив обе части уравнения А∙Х=В слева на матрицу
Отыскание решения системы по формуле (1) называется матричным способом решения системы. Формулы
Примеры: 1. Решить систему уравнений Запишем систему в виде А∙Х=В, где Решение матричного уравнения имеет вид Х =
Следовательно, 2. Решить по формулам Крамера систему уравнений
Для того, чтобы решить систему уравнений по формулам Крамера вычислим определитель системы
По формулам Крамера найдем значения переменных.
Ответ: Задание Вариант 1 Задача 1.Решить систему матричным методом Задача 2. Решить систему по формулам Крамера Вариант 2 Задача 1.Решить систему матричным методом Задача 2. Решить систему по формулам Крамера Вариант 3 Задача 1.Решить систему матричным методом Задача 2. Решить систему по формулам Крамера Вариант 4 Задача 1.Решить систему матричным методом Задача 2. Решить систему по формулам Крамера Вариант 5 Задача 1.Решить систему матричным методом а) Задача 2. Решить систему по формулам Крамера Вариант 6 Задача 1.Решить систему матричным методом Задача 2. Решить систему по формулам Крамера Содержание отчёта Отчёт о проделанной работе должен содержать: - название темы практического занятия; - цели практического занятия; - условие задачи; - подробное решение задачи; - ответ. Контрольные вопросы 1. При каком условии однородная система имеет нулевые решения? 2. Для каких систем применимы матричный метод и правило Крамера? 3. Каков алгоритм нахождения обратной матрицы? 4. Каков алгоритм решения систем линейных алгебраических уравнений матричным методом? 5. Как составляют определители при решении систем линейных алгебраических уравнений по формулам Крамера?
Литература: 1. Богомолов Н.В. Практические занятия по математике. – М.: «Высшая школа», 2002. с. 29 – 32 2. Шипачев В.С. Высшая математика: Учебник. – М.: Высшая школа, 2010г. с. 220-240 Практическое занятие № 16
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.123.182 (0.009 с.) |


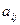 ,
, 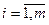 ,
, 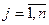 называют коэффициентами системы, числа
называют коэффициентами системы, числа  - свободными членами,
- свободными членами,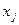 - неизвестные.
- неизвестные.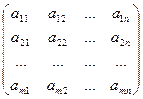 , Х =
, Х =  - вектор-столбец из неизвестных
- вектор-столбец из неизвестных  - вектор-столбец из свободных чисел
- вектор-столбец из свободных чисел  ,
, 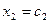 , …,
, …,  , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде вектор-столбца С =
, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде вектор-столбца С =  .
.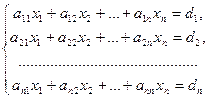
 такой матрицы называется определителем системы. Если определитель системы отличен от нуля
такой матрицы называется определителем системы. Если определитель системы отличен от нуля 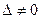 , то система имеет единственное решение.
, то система имеет единственное решение. (матрица обратная матрице А), получим
(матрица обратная матрице А), получим 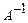 ∙ А = Е и Е∙Х = Х, то Х =
∙ А = Е и Е∙Х = Х, то Х =  ,
, 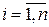 или
или 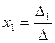 ,
, 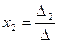 , …,
, …, 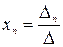 называются формулами Крамера, где
называются формулами Крамера, где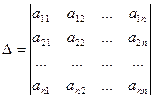 ,
,  ,
,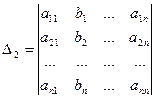 ,…,
,…, 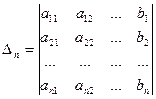
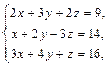 представив ее в виде матричного уравнения.
представив ее в виде матричного уравнения.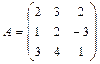 ,
, 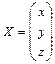 ,
, 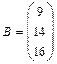 .
.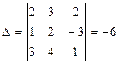 . Вычислим алгебраические дополнения элементов этого определителя:
. Вычислим алгебраические дополнения элементов этого определителя:  ,
, 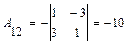 ,
, 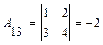 ,
, 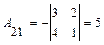 ,
,  ,
, 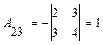 ,
, 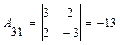 ,
,  ,
, 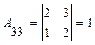 . Таким образом,
. Таким образом, 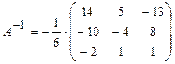 , откуда
, откуда .
.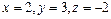 .
.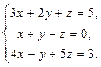
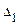 ,
, 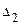 ,
, 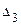 .
.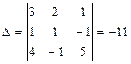 ,
,  ,
, 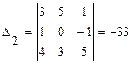 ,
, 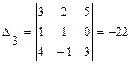 .
. ,
, 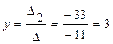 ,
, 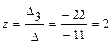 .
.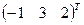 .
.