
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование простейших функций. Вычисление простейших определенных интегралов.
Цели: в результате выполнения практической работы, обучающиеся должны уметь применять свойства неопределенных и определенных интегралов, формулы интегрирования для нахождения неопределенных интегралов и вычисления определенных интегралов.
Пояснения к работе Неопределенный интеграл Функция Отыскание первообразной функции по заданной её производной есть действие, обратное дифференцированию, - интегрирование. Совокупность первообразных для функции Основные свойства неопределенного интеграла: 1. 2. 3. 4. Основные формулы интегрирования 1. Непосредственное интегрирование Непосредственное интегрирование основано на прямом использовании таблицы интегралов, свойств интегралов. Не всегда сразу можно применить таблицу интегралов, часто вначале для данной подынтегральной функции применяют элементарные тождественные преобразования, затем применяют свойства интегралов и только потом табличные интегралы. Например,
Замена переменной. Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла Найти следующие интегралы. 1) 2) В практике интегрирования часто встречаются интегралы, для нахождения которых можно, не производя подробного решения методом подстановки, использовать формулу Определенный интеграл. Пусть функция Определенным интегралом от функции f(x) на отрезке [ a; в ] называют предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю
Если функция f(x) непрерывна на [ a;b ], то предел интегральной суммы всегда существует и не зависит от способа разбиения отрезка [ a;b ] на элементарные отрезки и от выбора точек Для вычисления определенного интеграла от функции
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.202.4 (0.004 с.) |
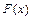 называется первообразной для функции
называется первообразной для функции  в промежутке
в промежутке 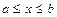 , если в любой точке этого промежутка её производная равна
, если в любой точке этого промежутка её производная равна 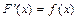 .
. . Таким образом,
. Таким образом, 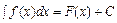 . Здесь
. Здесь 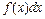 - подынтегральное выражение; С – произвольная постоянная.
- подынтегральное выражение; С – произвольная постоянная.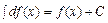 .
. ;
;  .
.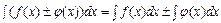 .
. .
.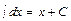 ; 2.
; 2. 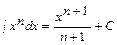 ; 3.
; 3.  ; 4.
; 4. 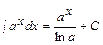 ; 5.
; 5. 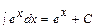 ; 6.
; 6. 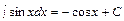 ; 7.
; 7. 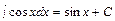 ; 8.
; 8.  ; 9.
; 9. 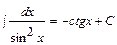 ; 10.
; 10. 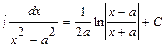 ; 11.
; 11.  ; 12.
; 12.  ; 13.
; 13. 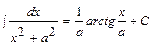 .
.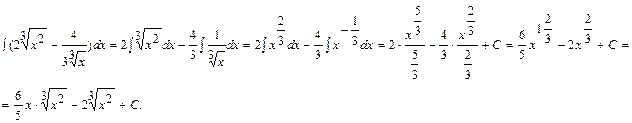
 , который легко вычисляется по какой-либо из основных формул интегрирования. Формула замены переменной имеет вид
, который легко вычисляется по какой-либо из основных формул интегрирования. Формула замены переменной имеет вид  где
где 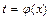 .
.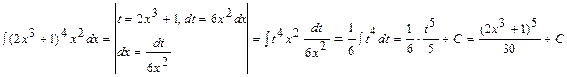 .
. .
.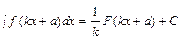 . Например,
. Например, 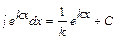 ,
, 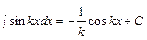 ,
, 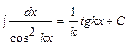 .
.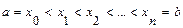 . Выберем на каждом элементарном отрезке
. Выберем на каждом элементарном отрезке 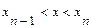 произвольную точку
произвольную точку 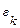 , и вычислим значение функции в точках
, и вычислим значение функции в точках 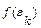 . Обозначим длину каждого элементарного отрезка
. Обозначим длину каждого элементарного отрезка 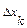 . Интегральной суммой для функции
. Интегральной суммой для функции  .
. .
.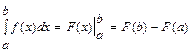 , т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
, т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.


