
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение линейных дифференциальных уравнений первого порядка и линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Цели: в результате выполнения практической работы, обучающиеся должны уметь приводить линейные дифференциальные уравнения первого порядка к уравнению с разделяющимися переменными; уметь составлять и решать характеристическое уравнение линейного дифференциального уравнения второго порядка с постоянными коэффициентами и применять соответствующую формулу для нахождения общего решения дифференциального уравнения; находить частное решение. Пояснения к работе Уравнение вида Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки Если выполнить подстановку
Сгруппируем второе и третье слагаемые в левой части уравнения Найдем функцию
Найти частное решение уравнения: Решение: данное уравнение является линейным. Пусть Найдем функцию Это уравнение с разделяющимися переменными. Разделим переменные уравнения Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами называют уравнение вида Для отыскания общего решения данного уравнения составляют характеристическое уравнение
Общее решение данного уравнения строится в зависимости от корней характеристического уравнения. Возможны три случая: 1). Дискриминант уравнения 2). Дискриминант уравнения 3). Дискриминант уравнения Найти частное решение уравнения Решение. Составим характеристическое уравнение и найдем его корни Для нахождения искомого частного решения нужно определить значения постоянных Задание Вариант 1 Задача 1. Найдите общее решение дифференциального уравнения: а) Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: Вариант 2 Задача 1. Найдите общее решение дифференциального уравнения: а) Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: Вариант 3 Задача 1. Найдите общее решение дифференциального уравнения: а) Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: Вариант 4 Задача 1. Найдите общее решение дифференциального уравнения: а) Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию:
Вариант 5 Задача 1. Найдите общее решение дифференциального уравнения: а) Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: Вариант 6 Задача 1. Найдите общее решение дифференциального уравнения: а) Задача 2. Найдите частное решение дифференциального уравнения, удовлетворяющее данному начальному условию: Содержание отчёта Отчёт о проделанной работе должен содержать: - название темы практического занятия; - цели практического занятия; - условие задачи; - подробное решение задачи; - ответ. Контрольные вопросы 1. Каков алгоритм решения линейных дифференциальных уравнений первого порядка? 2. Каков алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами? 3. Что является решением дифференциального решения? 4. Как находят частное решение дифференциального уравнения?
Литература: 1. Богомолов Н.В. Практические занятия по математике. – М.: «Высшая школа» 2002. с. 248 – 255 2. Омельченко В.П., Курбатова Э.В. Математика. - Ростов-на-Дону: «Феникс» 2011.- с. 167 – 174.
Практическое занятие № 9 Решение прикладных задач Цели: в результате выполнения практической работы, обучающиеся должны уметь по условию задачи составлять дифференциальные уравнения, выбирать метод решения дифференциального решения, находить общее или частное решение. Пояснения к работе Дифференциальные уравнения относятся к классу функциональных, когда неизвестной является функция, причем в записи уравнения эта функция находится под знаком производной. Дифференциальные уравнения имеют большое прикладное значение, с их помощью можно описывать (моделировать, изучать) процессы. Производная некоторой функции есть скорость изменения этой функции. Поэтому дифференциальные уравнения могут моделировать химические реакции, рост растений, изменение численности бактерий и популяций животных, перетекание тепла, энергии и т.д. Например, известный второй закон Ньютона При решении практических задач составляют дифференциальное уравнение в котором связаны искомая функция, независимая переменная и производная этой функции. Которое решают одним из известных методом. Например, скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Температура воздуха равна Решение. Скорость охлаждения есть скорость изменения температуры со временем и поэтому выражается в виде производной С другой стороны, на основании закона охлаждения, данного в задаче, скорость тела может быть представлена выражением Приравнивая два выражения, определяющих скорость охлаждения тела, приходим к дифференциальному уравнению
Чтобы ответить на вопрос, поставленный в задаче, надо пользуясь найденной функцией, описывающей зависимость температуры тела от времени, надо найти t при Т = Составить уравнение кривой, проходящей через точку М(2; -1) и имеющей касательную с угловым коэффициентом Решение. Согласно условию, имеем Задание Вариант 1 Задача 1. Составить уравнение кривой, проходящей через точку М(1; 2) и имеющей угловой коэффициент Задача 2. В воде с температурой
Вариант 2 Задача 1. Составить уравнение кривой, проходящей через точку М(2; 1) и имеющей угловой коэффициент Задача 2. Температура воздуха
Вариант 3 Задача 1. Составить уравнение кривой, проходящей через точку М(2; 1) и имеющей угловой коэффициент Задача 2. Температура воздуха
Вариант 4 Задача 1. Составить уравнение кривой, проходящей через точку М(2; 2) и имеющей угловой коэффициент Задача 2. Вода в открытом резервуаре сначала имела температуру
Вариант 5 Задача 1. Составить уравнение кривой, проходящей через точку М(0;1), если угловой коэффициент касательной в любой точке кривой равен произведению координат точки касания. Задача 2. Вращающийся в жидкости диск замедляет свою угловую скорость за счет трения, причем сила трения пропорциональна угловой скорости. Определите: скорость вращения диска в момент t = 120 с, если при t = 0 он вращался со скоростью 12 рад/с, а при t = 10 с его скорость стала 8 рад/с; момент времени, скорость диска окажется равной 1 рад/с. Вариант 6 Задача 1. Составить уравнение кривой, проходящей через точку М(1;2), если угловой коэффициент касательной в любой точке кривой равен Задача 2. Замедляющее трение на диск, вращающейся в жидкости, пропорционально угловой скорости. Определите: в какой момент времени скорость вращения диска окажется равной 2 рад/с, если при t = 0 он вращался со скоростью 20 рад/с, а при t = 8 с его скорость стала 16 рад/с; скорость вращения диска в момент времени t = 12 с.
Содержание отчёта Отчёт о проделанной работе должен содержать: - название темы практического занятия; - цели практического занятия; - условие задачи; - подробное решение задачи; - ответ. Контрольные вопросы 1. Что является решением дифференциального уравнения? 2. В чем состоит задача Коши? 3. Объясните геометрический смысл общего решения дифференциального уравнения. 4. Объясните геометрический смысл частного решения.
Литература: 3. Богомолов Н.В. Практические занятия по математике. – М.: «Высшая школа» 2002. с. 245 – 248. 4. Омельченко В.П., Курбатова Э.В. Математика. - Ростов-на-Дону: «Феникс» 2011.- с. 174 – 179.
Практическое занятие № 10
|
||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.22.244 (0.077 с.) |
 или
или  , где
, где  и
и  – функции переменной х, называют линейным дифференциальные уравнения первого порядка. В частности
– функции переменной х, называют линейным дифференциальные уравнения первого порядка. В частности  , где
, где  и
и 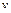 – новые функции от переменной
– новые функции от переменной  .
.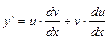 и уравнение примет вид
и уравнение примет вид
 (*)
(*) .
.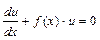 . Это уравнение с разделяющимися переменными. Разделим переменные
. Это уравнение с разделяющимися переменными. Разделим переменные  . Проинтегрируем обе части уравнения
. Проинтегрируем обе части уравнения  ;
;  , где
, где 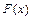 – первообразная функции
– первообразная функции  . Значит,
. Значит,  . Подставим найденную функцию в уравнение (*), получим уравнение
. Подставим найденную функцию в уравнение (*), получим уравнение  . Это уравнение с разделяющимися переменными. Разделим переменные
. Это уравнение с разделяющимися переменными. Разделим переменные  . Проинтегрируем обе части уравнения
. Проинтегрируем обе части уравнения  ;
;  . Тогда искомая функция равна
. Тогда искомая функция равна  .
. , если
, если  .
. . Сгруппируем второе и третье слагаемые в левой части уравнения
. Сгруппируем второе и третье слагаемые в левой части уравнения  . (*)
. (*) . Это уравнение с разделяющимися переменными. Разделим переменные
. Это уравнение с разделяющимися переменными. Разделим переменные  . Проинтегрируем обе части уравнения
. Проинтегрируем обе части уравнения  ;
;  , т. е.
, т. е.  . Подставим найденную функцию в уравнение (*), получим уравнение
. Подставим найденную функцию в уравнение (*), получим уравнение  .
. . Проинтегрируем обе части
. Проинтегрируем обе части ;
;  . Тогда искомая функция равна
. Тогда искомая функция равна  – общее решение. Найдем частное решение, для чего найдем С.
– общее решение. Найдем частное решение, для чего найдем С.  ,
,  . Значит, частное решение –
. Значит, частное решение –  .
. или
или 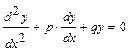 , где p и q – постоянные величины.
, где p и q – постоянные величины. , которое получается из данного уравнения заменой
, которое получается из данного уравнения заменой  ,
,  и
и  на соответствующую степень переменной
на соответствующую степень переменной  , причем сама функция
, причем сама функция  и
и  . В этом случае общее решение уравнения имеет вид
. В этом случае общее решение уравнения имеет вид 
 .
. и
и  . В этом случае общее решение уравнения имеет вид
. В этом случае общее решение уравнения имеет вид  .
. , если
, если  и
и  при
при  .
. ,
,  , значит, характеристическое уравнение имеет два различных действительных корня:
, значит, характеристическое уравнение имеет два различных действительных корня:  и
и  . Общее решение уравнения имеет вид
. Общее решение уравнения имеет вид  .
. и
и  . Найдем производную общего решения
. Найдем производную общего решения  . Подставим начальные условия в общее решение и в его производную, получим систему уравнений:
. Подставим начальные условия в общее решение и в его производную, получим систему уравнений: 
 ,
,  ,
,  . Значит, по формулам Крамера
. Значит, по формулам Крамера  ,
,  . Следовательно, частное решение имеет вид –
. Следовательно, частное решение имеет вид –  .
. , б)
, б)  .
. , если y = 3, y′ = 0 при х = 0.
, если y = 3, y′ = 0 при х = 0. , б)
, б)  .
. , если y = 4, y′ = 10 при х = 0.
, если y = 4, y′ = 10 при х = 0. , б)
, б)  .
. , если y= 1 и y΄= 1 при х = 0.
, если y= 1 и y΄= 1 при х = 0. , б)
, б)  .
. , если y= 2 и y΄= 9 при х = 0.
, если y= 2 и y΄= 9 при х = 0. , б)
, б)  .
. , если y = 1 и y΄= 1 при х = 0.
, если y = 1 и y΄= 1 при х = 0. , б)
, б)  .
. , если y= 1 и y΄= 5 при х = 0.
, если y= 1 и y΄= 5 при х = 0. фактически представляет дифференциальное уравнение второго порядка
фактически представляет дифференциальное уравнение второго порядка  .
. С. Известно, что в течении20 мин. Тело охлаждается от
С. Известно, что в течении20 мин. Тело охлаждается от 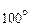 С до
С до  С. В течение какого времени тело охладится до температуры
С. В течение какого времени тело охладится до температуры  ?
? , где через Т обозначена температура тела, а через t – время.
, где через Т обозначена температура тела, а через t – время. , где k – коэффициент пропорциональности.
, где k – коэффициент пропорциональности. . Разделим переменные:
. Разделим переменные:  . Интегрируя почленно, получаем:
. Интегрируя почленно, получаем:  ,
,  или
или  ,
,  ,
,  . Найдем значения С и k, мы знаем, что при t = 0 температура тела T =
. Найдем значения С и k, мы знаем, что при t = 0 температура тела T =  , т. е.
, т. е.  . Следовательно,
. Следовательно,  . Нам известно, что в течение 20 мин. Тело охлаждается до
. Нам известно, что в течение 20 мин. Тело охлаждается до  температура
температура  . Имеем:
. Имеем:  ,
,  ,
,  ,
,  ,
,  ,
,  , т.е.
, т.е.  ,
,  ,
,  .
. ,
,  ,
,  ,
, 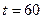 . Ответ: 60 мин.
. Ответ: 60 мин. .
. . Проинтегрировав, получим
. Проинтегрировав, получим  ,
,  . С учетом начальных условий
. С учетом начальных условий  и
и  , находим
, находим  , С = – 7. Следовательно, уравнение кривой имеет вид
, С = – 7. Следовательно, уравнение кривой имеет вид  . Ответ:
. Ответ:  в любой точке касания.
в любой точке касания. в любой точке касания.
в любой точке касания. . Известно, что за 30 минут тело охладится от
. Известно, что за 30 минут тело охладится от  до
до  С. Какой будет температура через час после первоначального измерения, если по закону Ньютона скорость охлаждения пропорциональна разности температур тела и окружающей среды?
С. Какой будет температура через час после первоначального измерения, если по закону Ньютона скорость охлаждения пропорциональна разности температур тела и окружающей среды? . Известно, что за 40 минут тело охладится от
. Известно, что за 40 минут тело охладится от  до
до  ?
? в любой точке касания.
в любой точке касания. . Через 10 минут температура воды стала
. Через 10 минут температура воды стала  , температура окружающей среды
, температура окружающей среды  С. Определите температуру воды в резервуаре через 30 минут от первоначального измерения, если по закону Ньютона скорость охлаждения пропорциональна разности температур тела и окружающей среды, когда температура воды в резервуаре станет равной
С. Определите температуру воды в резервуаре через 30 минут от первоначального измерения, если по закону Ньютона скорость охлаждения пропорциональна разности температур тела и окружающей среды, когда температура воды в резервуаре станет равной  .
.


