
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о баке с наименьшей площадью поверхности.Содержание книги
Поиск на нашем сайте
Требуется найти высоту h0 и радиус r0 жестяного бака объема V = 30 м3, имеющего форму закрытого кругового цилиндра, при которых площадь его поверхности S минимальна (в этом случае на его изготовление пойдет наименьшее количество жести). 1. Построение модели. Запишем следующие формулы для объема и площади поверхности цилиндра высоты h и радиуса r:
Выражая h через r и V из первой формулы и подставляя полученное выражение во вторую, получим:
2. Решение математической задачи, к которой приводит модель. С математической точки зрения, задача сводится к определению такого значения r, при котором достигает своего минимума функция S(r). Найдем те значения r0, при которых производная 3. Интерпретация полученных следствий из математической модели. На изготовление цилиндрического бака пойдет меньше всего жести, если у него будет радиус Транспортная задача. В городе имеются два склада муки и два хлебозавода. Ежедневно с первого склада вывозят 50 т муки, а со второго – 70 т на заводы, причем на первый – 40 т, а на второй – 80 т. Обозначим через aij стоимость перевозки 1 т муки с i -того склада на j -тый завод (i,j = 1,2). Пусть а11 = 1,2 р., а12 = 1,6 р., а21 = 0,8 р., а22 = 1 р. Как нужно спланировать перевозки, чтобы их стоимость была минимальной? 1. Построение модели. Придадим задаче математическую формулировку. Обозначим через х11 и х12 количество муки, которое надо перевезти с первого склада на первый и второй заводы, а через х21 и х22 – со второго склада на первый и второй заводы соответственно. Тогда получим следующую систему уравнений:
Общая стоимость всех перевозок определяется формулой: f = 1,2x11 + 1,6x12 +0,8x21 + x22. С математической точки зрения задача заключается в том, чтобы найти четыре числа х11, х12, х21 и х22, удовлетворяющие всем заданным условиям и дающие минимум функции f. 2. Решение математической задачи, к которой приводит модель. Решим систему уравнений (1) относительно хij (i,j = 1, 2) методом исключения неизвестных (метод Гаусса). Получим, что
а х22 не может быть определено однозначно. Так как Эта функция линейная, с угловым коэффициентом k = -0,2 < 0. Следовательно, она убывает на всем промежутке [30; 70]. Значит, свое наименьшее (минимальное) значение эта функция принимает при х22 = 70. Соответствующие значения других неизвестных определяем с помощью системы (2): х11 = 40, х12 = 10, х21 = 0. 3. Интерпретация полученных следствий из математической модели. Стоимость перевозок будет минимальной, если с первого склада на первый хлебозавод будет поставляться 40 т муки, на второй хлебозавод – 10 т муки, а вся мука со второго склада будет поставляться только на второй хлебозавод.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.108.200 (0.009 с.) |

 ,
, 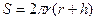 .
. .
. обращается в ноль:
обращается в ноль:  . Можно проверить, что вторая производная функции S(r) меняет знак с минуса на плюс при переходе аргумента r через точку r0 ., следовательно, в точке r0 функция S(r) имеет минимум. Соответствующее значение h0 = 2r0. Подставляя в выражение для r0 и h0 заданное значение V, получим искомый радиус
. Можно проверить, что вторая производная функции S(r) меняет знак с минуса на плюс при переходе аргумента r через точку r0 ., следовательно, в точке r0 функция S(r) имеет минимум. Соответствующее значение h0 = 2r0. Подставляя в выражение для r0 и h0 заданное значение V, получим искомый радиус  и высоту
и высоту  .
.

 (i,j = 1,2), то из системы (2) следует, что
(i,j = 1,2), то из системы (2) следует, что  . Подставляя выражения из системы (2) для х11, х12, х21 в формулу для f, получим f = 148 – 0,2х22.
. Подставляя выражения из системы (2) для х11, х12, х21 в формулу для f, получим f = 148 – 0,2х22.


