Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор нескольких элементов. Размещения. Сочетания
В предыдущем параграфе все примеры и упражнения сводились к выбору одного элемента из данного множества и подсчету количества таких выборов. А если необходимо выбрать б о льшее число элементов данного множества? Начнем со случая выбора двух элементов. Пример 10. В чемпионате участвовали 7 команд. Каждая команда играла один матч с каждой. Сколько всего было встреч? Решение. Рассмотрим таблицу результатов встреч размером 7x7 (рис. 4.4).
Рисунок 4.4 Коротко решение задачи выглядит так:
Ответ: 21. Около 2500 лет тому назад древнегреческие математики находили сумму 1 + 2 + 3 +... + (п – 1) + п с помощью примерно таких же рассуждений. Сначала они рисовали клетчатую лесенку, в основании которой – полоса из п клеток, над ней полоса, в которой (п – 1) клетка, затем полоса с (п – 2) клетками, и т. д.; в предпоследней строке стояли две клетки, а наверху – одна клетка. Правее они рисовали ту же лесенку, но в перевернутом виде: внизу – одна клетка, над ней – две, затем – три клетки,..., а последняя строка состоит из п клеток (рис. 4.5). Затем, сдвинув эти лесенки вместе, получали прямоугольник из п строк и (п + 1) столбца (рис. 4.6). Рисунок 4.5
Получилась замечательная формула для суммы первых п натуральных чисел: Рисунок 4.6
Замечание. С помощью этой формулы можно несколько по иному найти сумму первых п членов арифметической прогрессии:
Вернемся к примеру 10. Состав участников игры определен, как только мы выбрали две команды. Значит, количество всех игр в турнире из п команд – это в точности количество всех выборок двух элементов из п данных элементов. Важно при этом то, что порядок выбора не имеет значения, т. е. если выбраны две команды, то какая из них первая, а какая вторая – не важно.
Пример 11. Встретились 6 друзей и каждый пожал руку каждому своему другу. Сколько было рукопожатий? Решение. Первый способ. Можно, как и в примере 1, составить таблицу рукопожатий 6 друзей. Затем, рассуждая аналогично, получим, что общее число рукопожатий равно Второй способ. Условно перенумеруем друзей. Первый поздоровался со вторым, третьим,..., шестым. Всего 5 рукопожатий. Для второго неучтенными остались рукопожатия с третьим, четвертым, пятым, шестым. Всего 4 рукопожатия, и т. д. (рис. 4.7). Получаем, что рукопожатий было всего 5 + 4 + + 3 + 2 + 1 = 15. Ответ: 15.
Рисунок 4.7
Подведем промежуточный итог, оформив его в виде теоремы. ТЕОРЕМА (о выборках двух элементов). Если множество состоит из п элементов, то у него имеется Иными словами, если множество состоит из п элементов и требуется выбрать из них два элемента без учета их порядка, то такой выбор можно произвести Пример 12. В классе 27 учеников. К доске нужно вызвать двоих. Сколькими способами это можно сделать, если: а) первый ученик должен решить задачу по алгебре, а второй – по геометрии; б) они должны быстро стереть с доски? Решение. Для стирания с доски порядок вызова учеников не важен, т. е., к примеру, вызов Коли и затем Кати ничем не отличается от вызова Кати и затем Коли. А вот в первом случае порядок существенен (по крайней мере, для Кати и Коли). Тут применимо правило умножения. Учитель сначала вызывает решать алгебраическую задачу одного из 27 учеников, а затем независимым образом вызывает одного из оставшихся 26 учеников решать задачу по геометрии. Получается 27 • 26 = 702 способа вызова. Если во втором случае начать считать, как и в первом, то любую пару учеников мы посчитаем дважды. Например, сначала Коля, потом Катя, или сначала Катя, потом Коля. Значит, количество вызовов без учета порядка будет ровно в два раза меньше, чем количество вызовов с учетом порядка. Ответ: а) 702; 6) 351. Это рассуждение верно и в общем случае выбора двух элементов из п данных. Оказывается, что всегда количество выборок двух элементов без учета порядка будет ровно в два раза меньше, чем количество выборок с учетом порядка. На рисунке представлена соответствующая схема (рис. 4.8).
Рисунок 4.8 Из схемы мы видим, что комбинации, связанные с выбором двух элементов из п элементов, отличаются тем, что в некоторых из них важен порядок выбора элементов, а в некоторых – нет. Комбинации первого типа называются размещениями, а второго – сочетаниями. Для произвольного числа элементов определения комбинаций будут иметь следующий вид: Комбинации из п элементов по т элементов, которые отличаются друг от друга самими элементами или их порядком, называются размещениями. Обозначается
Сочетаниями называются все комбинации из п элементов по т, которые отличаются друг от друга по крайней мере хотя бы одним элементом (т и п – натуральные числа, т ≤ п).
Символы Пример 13. В классе 27 учеников, из которых нужно выбрать троих. Сколькими способами это можно сделать, если: а) первый ученик должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую; б) им следует спеть хором? Решение. Рассуждаем, как в примере 3. В первом случае важен порядок вызова учеников и применимо правило умножения. Один из 27 учеников идет решать задачу. Один из оставшихся 26 учеников идет за мелом, а один ученик из оставшихся 25 будет дежурным в столовой. Получается: 27 • 26 • 25 = 17550 способов вызова. Во втором случае начнем действовать, вызывая учеников по порядку. Можно сначала вызвать Пашу, затем Вову и потом — Асю. Обозначим этот вариант (ПВА). Можно вызывать этих же ребят в другом порядке. Например, сначала Асю, затем Пашу и потом — Вову (АПВ). Буквы А, П, В можно расставить по порядку ровно Р3 = 3! способами. Во всех этих случаях состав хора будет одним и тем же. Значит, каждый состав хора при подсчете, учитывающем порядок вызова учеников, мы возьмем 3! раз. Поэтому количество различных составов хора в 3! раз меньше количества всех вызовов по порядку. Итак, число способов, при которых порядок выбора трех элементов из 27 не важен, в 3! раз меньше числа способов, при которых порядок выбора трех элементов из 27 важен. Остается лишь учесть, что 3! = 3 • 2 • 1 = 6, и получить ответ: Ответ: а) 17550; б) 2925. Пример 14. «Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». Мишке поручили принести со склада 8 каких-нибудь попавшихся под лапы музыкальных инструментов из имеющихся 13 инструментов. Сколько способов выбора есть у Мишки? Решение. По условию порядок выбора не важен. Значит, нам требуется найти количество всех выборок 8 элементов из 13 данных без учета порядка, то есть число сочетаний из 13 элементов по 8:
Ответ: 1287. Теперь посмотрим на число Возникает вопрос: что же такое «ноль факториал»? Математики поступили просто. Чтобы сохранить красивую и очень удобную формулу для чисел
Тогда Действительно, 0 элементов из п данных можно «выбрать» единственным способом — ничего не выбирая. Справедлива формула В самом деле, Как видите, числители в обоих случаях одинаковы, а в знаменателе множители поменялись местами, что, естественно, не отражается на числовом значении выражения. В чем польза полученной формулы? Представьте себе, что надо вычислить Рассмотрим пример, в котором используется и правило умножения из предыдущего параграфа, и теорема о числе сочетаний, полученная в этом параграфе. Пример 15. Собрание из 80 человек выбирает председателя, секретаря и трех членов редакционной комиссии. Сколькими способами это можно сделать? Решение. Председателем может быть любой из участников собрания — 80 вариантов. Если председатель выбран, то секретарем может оказаться любой из оставшихся 79 человек — 79 вариантов. По правилу умножения получаем, что выбор председателя и секретаря осуществляется 80 • 79 = 6320 способами. Если испытание А – выбор председателя и секретаря – завершено, то следует заняться испытанием Б – выбором трех членов редакционной комиссии из оставшихся 78 участников собрания. Редакционную комиссию выбирают списком, т. е. порядок выбора не имеет значения. Сделать это можно Поскольку испытания А и Б предполагаются независимыми, остается лишь применить правило умножения: 6320 · 76076 = 480800320. Ответ: 480800320 способов. В тексте этого параграфа встречаются слова «выбор» и «выборка». Во избежание путаницы подчеркнем, что «выбор», как правило, означает сам процесс или факт совершения процесса выбирания. А «выборка» – это тот конкретный объект, который мы выбрали: выборка – это результат выбора. Подведем краткие итоги этого параграфа. Основной объект изучения в нем – числа Соберем вместе полученные сведения о числах
Для чисел
Основная закономерность образования строк в этом треугольнике состоит в следующем: каждое число в треугольнике Паскаля равно сумме двух чисел, стоящих над ним в предыдущей строке.
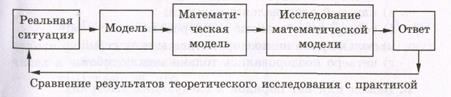
В заключение нашего знакомства с началами комбинаторики несколько слов о соотношении между реальными жизненными ситуациями и приведенными выше примерами и задачами. Во всех упражнениях мы осуществляли независимый выбор элементов. Но возможно ли такое в реальном мире? Вряд ли вы выберете, подобно Вове, из примера 2, кефир и бутерброд, особенно если бутерброд будет с соленой рыбой. Так в чем же дело? Неужели мы выбрали неверный подход к решению задач? И как тогда решать подобные задачи? Ну, невозможно же перебирать все мыслимые варианты, и каждый из них анализировать, реален он или нет. Такие же вопросы мучили и людей, живших задолго до нас, поэтому придумали реальную ситуацию «вставлять» в рамки модели, т. е. строить упрощенный вариант жизненной проблемы, убирая на время ее решения те житейские неурядицы, которые независимые события могут превратить в зависимые. И именно за счет такого упрощения оказывается возможным получить ответ. Надо только точно понимать, что ответ относится к модели, а возможность применять этот ответ в реальной жизни следует проверять (рис. 4.9). Итак, реальные испытания вполне могут быть зависимыми между собой, а мы выбираем простейшие модели, в которых эти испытания предполагаются независимыми. И именно правило умножения помогает нам решать задачи про независимые проведения испытаний.
Рисунок 4.9 Не следует, конечно, думать, что такое «раздвоение» имеет место только в комбинаторных задачах. Например, при решении текстовых задач про «производительность труда» или про «пешехода» мы имеем дело с абстрактным заводом и абстрактным рабочим или же с путником, который с одинаковой скоростью и без устали шагает по прямолинейному шоссе. Когда в физике мы говорим о равномерном движении тела, то явно имеем дело с некоторой абстрактной моделью. Ведь в реальной жизни практически никакое физическое тело равномерно не движется никакое заметное время. Да и что такое физическое тело? Контрольные вопросы 1 Сформулируйте правило умножения. Примеры. 2 Что такое п- факториал? Примеры. 3 Что называется перестановками из п элементов? Примеры. 4 Какие комбинации называются размещениями? Примеры. 5 Какие комбинации называются сочетаниями? Примеры. 6 Запишите формулы для нахождения перестановок, размещений и сочетаний. 7 Сформулируйте правило сложения. Примеры.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.203 (0.04 с.) |
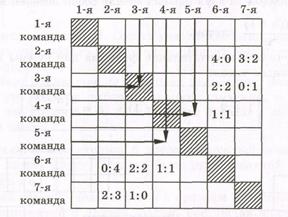 Так как никакая команда не играет сама с собой, то клетки по диагонали надо закрасить. Тогда в подсчете числа встреч будет участвовать ровно 72 - 7 = 7(7 - 1) = 42 клетки. В результате закрашивания таблица разделилась на две половинки, в них результаты встреч команд дублируются. Поэтому если мы разделим оставшиеся 42 клетки на две равные половины, то получим число всех проведенных игр.
Так как никакая команда не играет сама с собой, то клетки по диагонали надо закрасить. Тогда в подсчете числа встреч будет участвовать ровно 72 - 7 = 7(7 - 1) = 42 клетки. В результате закрашивания таблица разделилась на две половинки, в них результаты встреч команд дублируются. Поэтому если мы разделим оставшиеся 42 клетки на две равные половины, то получим число всех проведенных игр.
 Число клеток в этом прямоугольнике равно п (п + 1). Значит, в каждой из двух равных между собой лесенок находится п (п + 1) ровно
Число клеток в этом прямоугольнике равно п (п + 1). Значит, в каждой из двух равных между собой лесенок находится п (п + 1) ровно  клеток.
клеток.

 .
.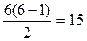 .
.
 подмножеств, состоящих из двух элементов.
подмножеств, состоящих из двух элементов.
 , где п – число всех имеющихся элементов, т – число элементов в каждой комбинации (т ≤ n).
, где п – число всех имеющихся элементов, т – число элементов в каждой комбинации (т ≤ n). .
.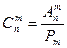 или
или  .
.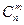 читаются в русской транскрипции так: «а из эн по эм» и «цэ из эн по эм» соответственно.
читаются в русской транскрипции так: «а из эн по эм» и «цэ из эн по эм» соответственно.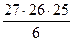 = 2925 способов.
= 2925 способов. .
.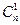 . С одной стороны, это количество выборок одного элемента из п данных, т. е., несомненно,
. С одной стороны, это количество выборок одного элемента из п данных, т. е., несомненно, 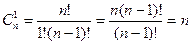 . Значит, и здесь имеется полное соответствие. А теперь посмотрим на число
. Значит, и здесь имеется полное соответствие. А теперь посмотрим на число  . По определению
. По определению  .
. , что отлично согласуется с комбинаторным определением
, что отлично согласуется с комбинаторным определением  ; получается, что
; получается, что 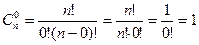 .
. .
.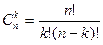 ,
,  .
.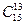 . Применив равенство
. Применив равенство 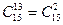 , мы упростим вычисления:
, мы упростим вычисления:  .
. способами:
способами:  .
. .
.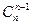 = п
= п
 имеется очень красивый и удобный способ записи – в виде треугольной таблицы, ее называют треугольником Паскаля.
имеется очень красивый и удобный способ записи – в виде треугольной таблицы, ее называют треугольником Паскаля.