
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отношения между множествами.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или диаграммами Эйлера – Венна). Для этого множества, сколько бы они ни содержали элементов, представляют в виде кругов или любых других замкнутых кривых (фигур) – рис.1.
Рис. 1.
1. Пусть даны два множества: X={a; b; c; d} иY={l; k; m; b; c}. Множества Х и Y содержат некоторые одинаковые элементы, а именно “b” и “c”. В данном случае говорят, что множества X иY находятся в отношении ПЕРЕСЕЧЕНИЯ. С помощью кругов Эйлера данное отношение можно представить в виде рис. 2.
Рис. 2. Рис. 3.
2. Пусть даны множества B1={1; 2; 3} и B2={4; 5; 6}. Данные множества различны, у них нет одинаковых элементов. В таком случае говорят, что множества B1 и B2 находятся в отношении НЕПЕРЕСЕЧЕНИЯ. С помощью кругов Эйлера данное отношение показано на рис. 3. 3. Пусть даны множества A={a; b; c; d; e} и B={a; b; c}. Очевидно, что эти множества пересекаются; кроме того, каждый элемент Определение 1.1
Отношение “включено” обозначается знаком Ì. Соответственно отношение “включает” – знаком É. Определение 1.1 символически записывается так: ВÌА или АÉВ. С помощью кругов Эйлера данное отношение между множествами показано на рис.4. Из определения подмножества следует, что всякое множества: Ø и А, которые называются НЕСОБСТВЕННЫМИ ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. Все остальные подмножества (если они существуют) называются СОБСТВЕННЫМИ ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. То есть, если В – собственное подмножество множества А, то имеем: ØÌ ВÌА, или иначе: АÉВÉ Ø. 4. Пусть даны множества C={x; y; z}, D={x; y; z}, которые состоят из одних и тех же элементов. В таком случае говорят, что множества С иD равны и пишут C=D. Определение 1.2 Множества С и D называются равными, если они состоят из одних и тех же элементов. Используя понятие “включено”, можно дать другое определение равенства множеств. Определение 1.3 Множества C и D называются равными тогда и только тогда, когда множество С является подмножеством множества D, и наоборот. Символически данное определение можно записать так:
С помощью кругов Эйлера отношение “равенство” показано на рис.5.
Рис.5. рис.6.
Универсальное множество. Пусть U (или T – total) – некоторое фиксированное множество. Рассмотрим только такие множества А, В, С,…, которые являются подмножествами множества U. В этом случае множество U называется универсальным множеством всех множеств А, В, С,… Примером универсального множества может служить множество действительных чисел, множество людей на планете Земля… Мы его будем изображать прямоугольником с буквой U в правом верхнем углу (рис.6), внутри которого будут размещаться те или иные множества.
Операции над множествами. Рассмотрим некоторые операции над множествами.
Пересечение множеств. Пусть даны два множества: А={a; b; c; d} и B={c; d; e}.образуем новое множество Р, состоящее из всех элементов, принадлежащих одновременно и множеству А, и множеству В, т.е. Р={c;d}. Тогда говорят, что множество Р является пересечением множеств А и В.
Определение 1.4 Пересечением множеств А и В называется множество, состоящее их всех тех и только тех элементов, которые принадлежат множествам А и В одновременно. Символически пересечение множеств А и В обозначается так: АÇВ, где символ Ç - знак пересечения множеств. Используя характеристическое свойство, определение 1.4 можно записать следующим образом:
Р=АÇВ= {x ïxÎA и xÎB}={x ï xÎA Ù xÎB}. (1)
Таким образом, (1) есть характеристическое свойство пересечения двух множеств. Союз “и” иногда заменяют фигурной скобкой, и тогда (1) будет иметь вид:
Для обозначения одновременной принадлежности множеству А и множеству В используется также знак Ù (конъюнкция, или логическое “и”):
xÎAÇB Þ xÎA Ù xÎB (2а)
Читаются выражения (2) и (2а) одинаково: если х принадлежит пересечению множеств А и В, то х принадлежит как множеству А, так и множеству В. Если мы имеем ситуацию, когда х не принадлежит пересечению множеств А и В, то это означает, что х не принадлежит или множеству А, или множеству В. Символически это может быть записано так:
где квадратная скобка заменяет союз “или”. В символической записи союз “или” может быть заменен также знаком Ú (дизъюнкция, логическое “или”):
хÏАÇВ Þ хÏА Ú хÏВ. (3а)
Читаются выражения (3) и (3а) одинаково: если х не принадлежит пересечению множеств А и В, то х не принадлежит или множеству А, или множеству В. Графическая иллюстрация вариантов пересечения двух множеств приведена на рис. 7¸10 (пересечение заштриховано).
рис. 7 рис. 8 рис. 9 рис. 10 Объединение множеств. Множества А и В входят в их объединение только один раз. Это вполне соответствует толкованию множества, принятому в математике: ни один элемент не может содержаться в множестве несколько раз. Определение 1.5 Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. Символически объединение двух множеств А и В обозначается так: А È В, где È - символ объединения множеств. Определение 1.5 можно записать с помощью характеристического свойства:
С= А È В={xï xÎA или xÎB}. (4)
Союз “или” иногда заменяют квадратной скобкой
а также знаком дизъюнкции
х ÎА È В Þ хÎА Ú хÎВ. (5а)
Читаются эти знаки одинаково: если элемент х принадлежит объединению двух множеств А и В, то он принадлежит множеству А или множеству В. Если же элемент х не принадлежит объединению множеств А и В, то он не принадлежит ни множеству А, ни множеству В. Символически это может быть записано так:
или
x ÏAÈB Þ xÏA Ù xÏB. (6а)
Графически варианты объединения двух множеств показаны на рис. 11\14 (объединение заштриховано).
рис. 11 рис. 12 рис. 13 рис. 14
Отметим некоторые очевидные свойства операции объединения двух множеств:
АÈА=А, АÈÆ=А, АÈU=U. (7)
Замечание1. Если А1, А2,…, Аn – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их пересечение, т.е. составляется множество, представляющее их общую часть:
Р= А1Ç А2Ç…Ç Аn={x ï xÎ" Ai, i=
Где символ " (квантор всеобщности) заменяет слово “все”, и, таким образом, мы символически обозначили ту часть множеств Ai, которая принадлежит каждому множеству одновременно.
Замечание 2. Если А1, А2,…, Аn – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их объединение – составляется множество, состоящее из элементов, которые принадлежат хотя бы одному их них:
C= A1ÈA2È…ÈAn={x ï xÎA1 или xÎA2 или …или xÎAn}.
Замечание 3. Если в выражении есть знаки È и Ç и нет скобок, то сначала выполняется операция пересечения, а потом – операция объединения (аналог сложению и умножению в арифметике).
Разность множеств.
Определение 1.6 Разностью двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В. Символически разность двух множеств обозначается так: А \ В, где символ \ является знаком разности для множеств. С помощью характеристического свойства запишем определение 1.6 следующим образом:
C=A \ B={x ï xÎA и xÏB} (8)
Или
а также xÎA\B Þ xÎA Ù xÏB. (9а)
Пример 1.
Если E1={2; 4; 6} и E2={6; 8; 10}, то E3=E1\E2={2; 4}, E4=E2\E1={8;10}.
Пример 2.
Если M1={x1; x2; x3}, M2={y1; y2}, то M3=M1\M2={ x1; x2; x3}, M4=M2\M1={y1; y2}.
Пример 3.
Если K1={1; 3; 5; 7; 9}, K2={5; 7; 1}, то K3=K1\K2={3; 9}, K4=K2\K1=Æ.
Графическое представление вариантов разности двух множеств А и В показано на рис. 15\18, где множество А \ В заштриховано.
рис. 15 рис. 16 рис. 17 рис. 18 Дополнение к множеству. Определение 1.7
Если ясно, о каком множестве идёт речь, то индекс А опускается и пишут
Определение 1.8 Пусть А – некоторое множество, являющееся частью универсального (основного) множества U. Дополнением множества А называется множество, состоящее из всех тех и только тех элементов их множества U, которые не принадлежат А. Его обозначают Это определение может быть записано в виде:
Графически дополнения (соответственно определениям 1.7 и 1.8) изображены на рис. 19 и 20 соответственно, на которых дополнения заштрихованы.
рис. 19 рис. 20
Тема 2. Матрицы 1о .Основные определения. Пусть Определение 1. Матрицей размеров
где Далее для изображения матрицы применяются либо круглые скобки, либо сдвоенные прямые:
Для краткого обозначения матрицы используется либо заглавная латинская буква Множество всех матриц размера Частные случаи матриц. 1. Если 2. Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е. 3. Диагональная матрица вида 4. Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается 5. Матрица размера 6. Если Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают. 2о. Операции над матрицами и их свойства. Определение 3. Суммой матриц Обозначение: Замечание. Сумма матриц – алгебраическая операция. Пример.
Свойства (сложения матриц). 1) Коммутативность сложения, т.е., 2) Ассоциативность сложения, т.е., 3) 4) Доказательство свойств – самостоятельно прямыми вычислениями. Теорема 1. Множество Доказательство следует из свойств 1)–4). Определение 4. Произведением элемента Обозначение: Операция, сопоставляющая Свойства (умножения матрицы на элемент кольца).
1) 2) 3) 4) Доказательство свойств – самостоятельно прямыми вычислениями. Замечание. Разность Определение 5. Произведением матриц Обозначение: Операция произведения Из определения следует, что элемент матрицы Примеры. 1) 2) Таким образом, две матрицы можно перемножать, если число столбцов матрицы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 4163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |







 X Y B1 B2
X Y B1 B2 Множество В является подмножеством множества А тогда и только тогда, когда каждый элемент множества В является элементом множества А.
Множество В является подмножеством множества А тогда и только тогда, когда каждый элемент множества В является элементом множества А. непустое множество А содержит по крайней мере два
непустое множество А содержит по крайней мере два

 (2)
(2) (3)
(3)



 (5)
(5) (6)
(6)



 },
},
 (9)
(9)



 или
или  .
. или
или  .
. или
или  .
.

 – коммутативное кольцо с единицей.
– коммутативное кольцо с единицей. над кольцом
над кольцом  элементов кольца
элементов кольца  строк и
строк и  столбцов:
столбцов:
 – номер строки,
– номер строки,  – номер столбца,
– номер столбца,  − элементы матрицы,
− элементы матрицы,  , то матрица называется квадратной, а число
, то матрица называется квадратной, а число  или
или  .
. , либо символы
, либо символы  ,
,  , либо с разъяснением:
, либо с разъяснением:  .
. .
. называется главной диагональю, а
называется главной диагональю, а  – побочной диагональю.
– побочной диагональю. .
. называется скалярной.
называется скалярной. или
или  , где
, где  .
.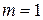 , то матрица называется строкой, или матрица-строка, или строка. Если
, то матрица называется строкой, или матрица-строка, или строка. Если 
 столбцовая = матрица-столбец = столбец.
столбцовая = матрица-столбец = столбец. и
и  (т.е. имеющих одинаковые порядки) называется матрица
(т.е. имеющих одинаковые порядки) называется матрица  :
:  .
. .
. .
. справедливо
справедливо 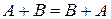 .
.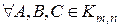 справедливо
справедливо  .
.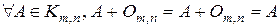 .
. . При этом, если
. При этом, если  , то
, то 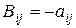 . Матрица
. Матрица  называется противоположной к
называется противоположной к  .
. относительно сложения образует абелеву группу.
относительно сложения образует абелеву группу. на матрицу
на матрицу  называется матрица
называется матрица 
 .
. и
и  называется умножением элемента кольца на матрицу.
называется умножением элемента кольца на матрицу. выполняется
выполняется .
.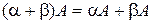 .
.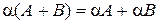 .
. .
. двух прямоугольных матриц
двух прямоугольных матриц  .
. размера
размера  называется матрица
называется матрица  размеров
размеров  такая, что каждый элемент
такая, что каждый элемент 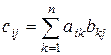 .
.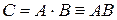 .
. , стоящий в
, стоящий в  –ой строке и
–ой строке и  –ом столбце, равен сумме произведений элементов
–ом столбце, равен сумме произведений элементов  ,
, .
. .
.


