
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Система линейных уравнений.
1о. Определения, обозначения. Определение 1. Системой
где Определение 2. Совокупность Определение 3. Если система (1) имеет хотя бы одно решение, то она называется совместной, если решений нет – несовместной. Пример. Определение 4. Два решения Определение 5. Если система (1) имеет единственное решение, то она называется определенной, если у системы существует по крайней мере два различных решения, то система называется неопределенной. Пример. Решить систему линейных уравнений – это значит выяснить, совместна она или нет, и в случае совместности найти все ее решения. Определение 6. Две системы линейных уравнений (СЛУ) с одинаковым числом неизвестных и над одинаковым полем называются эквивалентными, если они имеют одно и то же множество решений. СЛУ удобно записывать с помощью матрицы:
Матрица Если ввести
то систему (1) можно переписать в матричном виде
Наряду с основной матрицей
2о. Формулы Крамера. Рассмотрим частный случай, когда Теорема 1. (правило Крамера) Система
где
Формулы (3) называются формулами Крамера. Доказательство. Запишем систему в матричном виде (2):
т.к.
Тогда умножая (2) слева на
Здесь
Покажем, что это решение единственно. Пусть
Умножим первое уравнение на
Здесь коэффициенты при
Т.о., (3) дают единственное решение. Пример.
Замечание. Если рассматривать однородную СЛУ с Следствие. Если однородная система 3о. Условие совместности СЛУ. Теорема 2. (теорема Кронекерра–Капелли). Для того, чтобы система (1) была совместной, необходимо и достаточно, чтобы ранг ее расширенной матрицы был равен рангу основной матрицы, т.е.
Доказательство. Очевидно, что Для доказательства перепишем систему (1) в виде:
где выделены столбцы матрицы Необходимость. Если существует решение Достаточность. Пусть 4о. Построение решений СЛУ. Теорема Кронекера–Капелли устанавливает совместимость СЛУ, но не дает практического рецепта их нахождения. Ниже дается один из возможных способов. Пусть рассматривается произвольная система Определение 7. Число
Не ограничивая общности, будем считать, что базисный минор матрицы
Минор
(так как все решения (5) обращаются в тождество все последующие уравнения). Если Теорема 3. Если Пусть далее
Определение 8. Неизвестные Свободным переменным можно придать произвольные значения. Тогда базисные неизвестные
Здесь
Введем обозначения: Тогда имеем
Добавляя сюда очевидные равенства:
Формулы (7) дают общее решение системы (1), т. к. выражают все неизвестные Покажем, что формулы (7) содержат все варианты решения системы (1). В самом деле, если Таким образом, доказано. Теорема 4. Если (1) совместна и ее ранг меньше Пример.
5°. Метод Гаусса решения СЛУ. На практике чаще всего используют метод Гаусса построения решений СЛУ. При этом при исследовании и решении СЛУ производятся элементарные преобразования строк расширенной матрицы Замечание. Перестановка в основной матрице двух столбцов соответствует в системе перестановке неизвестных вместе со своими координатами. Умножение столбца на число и сложение столбцов приводит к изменению коэффициентов только при одном неизвестном и значит к системе, не эквивалентной рассматриваемой. Рассмотрим матрицу
( Выберем в матрице
Далее все элементы базисного минора выше главной диагонали можно сделать равными нулю (как в теореме 11, §11), а элементы главной диагонали – равными 1 (умножением строки на
Т.о., исходная система (1) приведена к эквивалентной системе
или к системе
Отсюда видно, что если
Если
или, по аналогии с (7)
По аналогии с п.4 можно показать, что (9), (10) дают общее решение системы (1). Итак, метод Гаусса состоит в следующем. 1) расширенную матрицу системы элементарными преобразованиями приводят к ступенчатому виду; 2) сравнивают ранги основной и расширенной матриц и делают вывод о совместности или не совместности системы; 3) в случае совместности системы в основной матрице выбирают базисный минор и дальнейшими элементарными преобразованиями строк добиваются того, чтобы в этом миноре все элементы вне главной диагонали стали равными нулю, а элементы главной диагонали стали равными единице; 4) выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, оставляя базисные неизвестные слева и переведя остальные слагаемые в правую часть; 5) если 6) если Пример (см. п.4°).
6°. Нахождение обратной матрицы методом Гаусса. Напомним, что матрица
Для этого воспользуемся определением обратной матрицы
…
Т.о., матричное уравнение
Все эти системы объединим в одной расширенной матрице:
Приведение этой матрицы к ступенчатому виду должно обозначать приведение к ступенчатому виду всех расширенных матриц подсистем. Так как
Решение каждой из подсистем имеет вид:
матрица Пример (см. пример из §8)
7о. Однородные системы уравнений. Рассмотрим однородную систему уравнений:
Лемма 1. Система однородных уравнений всегда совместна. Действительно, Ненулевые решения называются нетривиальными. В соответствии с общей теорией, справедлива следующая лемма. Лемма 2. Однородная система с квадратной матрицей Доказательство.
Теорема 5. (о множестве решений системы однородных уравнений). Множество решений СОЛУ образует в пространстве Доказательство. В соответствии с п.4о, решение СОЛУ можно записать в виде (см. формулу (7)):
т.к.
Следовательно, множество всех решений СОЛУ образует подпространство в пространстве Теперь покажем, что вектора
Снизу расположен минор порядка Пусть известны какие-либо
Тогда, в силу предыдущей теоремы, эти вектора образуют базис в подпространстве всех решений СОЛУ и любое решение может быть представлено в виде линейной комбинации этих векторов
и обратно, любая линейная комбинация дает решение СОЛУ. Определение 9. Всякая линейно независимая система Т.о., для того, чтобы решить СОЛУ, надо найти фундаментальную систему решений. Тогда общее решение задается формулой (11), где Пример.
Теперь покажем, что любое подпространство Теорема 6. Всякое подпространство
Доказательство. Пусть в
причем
Т.к. 8о. системы линейных неоднородных уравнений Рассмотрим систему неоднородных уравнений
Пусть
Вычитая из (13) выражение (14), получаем
Т.о., Пусть
Тогда получаем
Если Теорема 7. Общее решение СЛНУ (13) представляется в виде суммы произвольного частного решения этой системы и общего решения соответствующей ей однородной системы. Следствие 1. Разность двух произвольных решений СЛНУ является решением соответствующей СЛОУ. Следствие 2. Сумма любого частного решения СЛНУ с любым частным решением соответствующей СЛОУ дает частное решение СЛНУ. Замечание. В формуле (7) вектор
Тема 4. Линейное пространство
Пусть даны поле Определение 1. Множество 1) 2) Для любых а) Умножение б) в) Умножение вектора на скаляр дистрибутивно относительно сложения скаляров, т.е. г) Умножение вектора на скаляр дистрибутивно относительно сложения векторов, т.е. Обозначение. Замечание. Так как Свойствалинейного пространства. 1) 2)
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.2.122 (0.145 с.) |
 линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  над полем
над полем  называется система выражений вида
называется система выражений вида (1)
(1) . Элементы
. Элементы  называются коэффициентами системы (1),
называются коэффициентами системы (1),  – ее свободные члены. Если все
– ее свободные члены. Если все 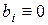 , то система (1) называется однородной, иначе – неоднородной.
, то система (1) называется однородной, иначе – неоднородной. называется решением (1), если после подстановки их вместо
называется решением (1), если после подстановки их вместо  соответственно во все уравнения (1) получаются тождества.
соответственно во все уравнения (1) получаются тождества. – несовместная.
– несовместная.  – совместная.
– совместная. являются различными, если нарушается одно из равенств
являются различными, если нарушается одно из равенств  , …,
, …,  .
. – неопределенная система.
– неопределенная система. ,
,  .
. называется основной матрицей системы (1) или матрицей системы (1).
называется основной матрицей системы (1) или матрицей системы (1). ,
,  ,
, (2)
(2) ,
, 
 и
и  , т.е.
, т.е.  , имеет решение, причем только одно. Это решение находится по формулам:
, имеет решение, причем только одно. Это решение находится по формулам: ,
,  , (3)
, (3) ,
,  – определитель матрицы, получаемой из
– определитель матрицы, получаемой из  -ого столбца на столбец свободных членов, т.е.
-ого столбца на столбец свободных членов, т.е. .
. – квадратная матрица и
– квадратная матрица и  определена обратная матрица
определена обратная матрица .
. , имеем:
, имеем: , т.е.
, т.е.
 .
. определяется через алгебраические дополнения к элементам
определяется через алгебраические дополнения к элементам  . Видно, что это можно переписать в виде формул (3).
. Видно, что это можно переписать в виде формул (3).
 , второе – на
, второе – на  , …, и сложим (здесь
, …, и сложим (здесь  – алгебраические дополнения к элементам
– алгебраические дополнения к элементам  -ого столбца матрицы
-ого столбца матрицы 
 равен
равен  , а остальные – нули, т.е.
, а остальные – нули, т.е.
 , т.е. те же формулы.
, т.е. те же формулы. .
.  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. и
и  .
. .
. .
. (4)
(4) , являющиеся элементами
, являющиеся элементами  .
. , равное рангу матриц
, равное рангу матриц  :
: .
. , …,
, …,  (5)
(5)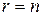 , то (5) система с определителем неравным нулю и она (и значит система (1)) имеет единственное решение, определяемое по правилу Крамера. Т.о., справедлива следующая теорема.
, то (5) система с определителем неравным нулю и она (и значит система (1)) имеет единственное решение, определяемое по правилу Крамера. Т.о., справедлива следующая теорема. , то система (1) имеет единственное решение.
, то система (1) имеет единственное решение. . Оставим в левых частях лишь те слагаемые, коэффициенты которых образуют базисный минор
. Оставим в левых частях лишь те слагаемые, коэффициенты которых образуют базисный минор  (6)
(6) называются базисными, а переменные
называются базисными, а переменные  – свободными.
– свободными. ,
, 
 – определитель, получающийся из
– определитель, получающийся из  заменой
заменой  -ого столбца на столбец свободных членов системы (6). Пользуясь свойствами определителя, последнюю формулу можно переписать в виде:
-ого столбца на столбец свободных членов системы (6). Пользуясь свойствами определителя, последнюю формулу можно переписать в виде: .
. ,
,  .
. .
. , …,
, …,  , имеем
, имеем (7)
(7) через свободные неизвестные
через свободные неизвестные  .
. , то эта система имеет бесконечное множество решений.
, то эта система имеет бесконечное множество решений.

 . Возьмем
. Возьмем  ,
, 
 .
. : перестановка строк (это соответствует перестановке уравнений системы), сложение строк (это соответствует сложению уравнений системы), умножение строк на отличное от нуля число (это соответствует умножению уравнения системы на отличное от нуля число). Очевидно, что при указанных преобразованиях получается система, эквивалентная данной. Следовательно, после элементарных преобразований строк расширенной матрицы
: перестановка строк (это соответствует перестановке уравнений системы), сложение строк (это соответствует сложению уравнений системы), умножение строк на отличное от нуля число (это соответствует умножению уравнения системы на отличное от нуля число). Очевидно, что при указанных преобразованиях получается система, эквивалентная данной. Следовательно, после элементарных преобразований строк расширенной матрицы  :
:  :
:
 – некоторый элемент поля
– некоторый элемент поля  ).
).  .
.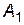 ненулевой минор порядка
ненулевой минор порядка  , т.е. базисный минор. Как и в теореме 11, §11 (о ступенчатой матрице), его можно выбрать на пересечении первых
, т.е. базисный минор. Как и в теореме 11, §11 (о ступенчатой матрице), его можно выбрать на пересечении первых  . Будем считать, что этот минор расположен в левом верхнем углу матрицы
. Будем считать, что этот минор расположен в левом верхнем углу матрицы  с любым решением).
с любым решением).  .
. ):
):


 , то система имеет единственное решение
, то система имеет единственное решение , …,
, …,  .
. , то переменные
, то переменные  , …,
, …,  , получим решение:
, получим решение: (9)
(9) (10)
(10) ,то в правой части стоят только свободные члены и получено единственное решение;
,то в правой части стоят только свободные члены и получено единственное решение; , то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение по формуле (9).
, то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение по формуле (9).
 ~
~  ~
~  ~
~ 

 называется обратной к
называется обратной к  . Обратные матрицы существуют лишь для невырожденных матриц, т.е.
. Обратные матрицы существуют лишь для невырожденных матриц, т.е.  . Было показано, что
. Было показано, что  , где
, где  – присоединенная матрица, полученная из алгебраических дополнений, т. е. вычислением определителей
– присоединенная матрица, полученная из алгебраических дополнений, т. е. вычислением определителей  -ого порядка. Вместе с тем, операция вычисления определителя, запрограммированная в ЭВМ, требует больших машинных ресурсов. Поэтому более предпочтительным выглядит вычисление обратной матрицы с помощью метода Гаусса.
-ого порядка. Вместе с тем, операция вычисления определителя, запрограммированная в ЭВМ, требует больших машинных ресурсов. Поэтому более предпочтительным выглядит вычисление обратной матрицы с помощью метода Гаусса.







 ;
;  ; …;
; …; 


 ,
,  , …,
, …, 
 , стоящая за вертикальной чертой, является обратной матрицей
, стоящая за вертикальной чертой, является обратной матрицей  ~
~  ~
~  ~
~  ~
~  ~
~ 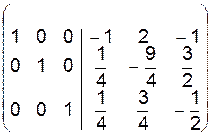

 – ее решение. Это решение называется тривиальным.
– ее решение. Это решение называется тривиальным. .
. Пусть нетривиальное решение существует, тогда два решения. Методом от противного. Пусть
Пусть нетривиальное решение существует, тогда два решения. Методом от противного. Пусть  Следовательно,
Следовательно,  подпространство размерности
подпространство размерности  , где
, где  .
. , т. е. в случае СОЛУ, любое решение системы выражается в виде линейной комбинации
, т. е. в случае СОЛУ, любое решение системы выражается в виде линейной комбинации  , …,
, …,  .
. – линейно независимы. Для этого составим матрицу
– линейно независимы. Для этого составим матрицу  из их координат:
из их координат:

 , …,
, …,  .
. ,
,  . (11)
. (11) – произвольные элементы
– произвольные элементы  ;
; 
 ~
~  .
. ,
,  .
. .
.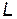 пространства
пространства  в пространстве
в пространстве  .
. и подпространство
и подпространство  . Возьмем в
. Возьмем в  дополним его до базиса в
дополним его до базиса в  . Каждый вектор
. Каждый вектор  можно разложить оп этому базису
можно разложить оп этому базису ,
,
 , т.к.
, т.к.  , …,
, …,  определяют
определяют  , где
, где  – матрица перехода,
– матрица перехода,  . Тогда
. Тогда 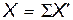 – формула связи координат вектора в различных базисах. Следовательно,
– формула связи координат вектора в различных базисах. Следовательно,  и система уравнений на
и система уравнений на  ,
,  (12)
(12) линейно независимы
линейно независимы  (13)
(13) . Пусть
. Пусть  – решение этой системы, т.е.
– решение этой системы, т.е. (14)
(14) .
. является решением соответствующего однородного уравнения.
является решением соответствующего однородного уравнения. – фундаментальная система решений однородного уравнения. Тогда любое
– фундаментальная система решений однородного уравнения. Тогда любое  может быть представлено в виде:
может быть представлено в виде: .
. (15)
(15) – частное решение СЛНУ, а вектора
– частное решение СЛНУ, а вектора  – частные решения СЛОУ.
– частные решения СЛОУ. 1о. Определение и простейшие свойства
1о. Определение и простейшие свойства ,
,  ,
,  , … и множество
, … и множество  элементов, называемых векторами и обозначаемых латинскими буквами
элементов, называемых векторами и обозначаемых латинскими буквами  . Введем на
. Введем на  ставит в соответствие третий элемент
ставит в соответствие третий элемент  , называемый суммой
, называемый суммой 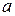 и
и  и обозначаемый
и обозначаемый  , а также операцию умножения скаляра на вектора, которая
, а также операцию умножения скаляра на вектора, которая  и
и  ставится в соответствие
ставится в соответствие  , называемый произведением вектора
, называемый произведением вектора 
 является абелевой группой;
является абелевой группой; и
и  выполняются равенства:
выполняются равенства: на
на  не изменяет
не изменяет  , т.е.
, т.е.  .
.

 .
.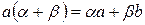 .
.
 .
. .
. , для каждого вектора
, для каждого вектора  существует единственный симметричный (противоположенный) элемент, обозначаемый
существует единственный симметричный (противоположенный) элемент, обозначаемый  , и для
, и для  имеет единственное решение
имеет единственное решение  , называемое разностью
, называемое разностью  выполняется
выполняется  .
. выполняется
выполняется  .
.


