
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства изоморфных пространств.
1. Нулевому элементу V соответствует нулевой элемент Доказательство: Если 2. Если элементам Доказательство следует из 1. 3. Если V и 4. Пространства разных размерностей не могут быть изоморфными. Теорема 6. Любые два Доказательство. Выберем в V базис Однако это соответствие взаимнооднозначно, т.к. В силу равноправности V и Таким образомо все линейные пространства данной размерности
Тема 5. Пространство геометрических векторов, как пример линейного пространства 1о. Направленные отрезки. Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ. Определение 1. Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец. Направленный отрезок обозначается Определение 2. Длиной
Рис.1. Направленный отрезок АВ. Определение 3. Направленные отрезки Направленные отрезки Направленные отрезки Каждую точку А пространства можно рассматривать как направленный отрезок с совпадающим началом и концом. Этот отрезок обозначается
Определение 4. Два направленных отрезка Эквивалентность является отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует: 1) отрезок 2) если 3) если
Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы – классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства. Определение 5. Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором). Замечание. Напомним, что в средней школе вектор характеризуетпараллельный перенос. Направление эквивалентных направленных отрезков называется направлением вектора, а их длина – длиной вектора. Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс эквивалентных направленных отрезков. Поэтому часто будем пишут вектор Определение 6. Вектор a такой, что Определение 7. Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают Нулевой вектор считается коллинеарным любому вектору. Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны. Определение 8. Три и более векторов называются компланарными, если они параллельны некоторой плоскости. Для определенности любую тройку векторов, содержащую нулевой вектор, считают комплонарной. Пусть даны два вектора a и b. Из произвольной точки O пространства отложим
Покажем, что вектор Определение 9. Вектор Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма. Свойства сложения векторов. 1. 2. 3. 4. Для каждого вектора
 а) б) а) б)
Рис.2. Свойства сложения векторов: а) коммутативность, б) ассоциативность Если Определение 10. Произведением вектора 1) векторы 2) Произведение вектора на число 0 есть нулевой вектор. Пишут
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.8.247 (0.011 с.) |
 и наоборот.
и наоборот. .
.
 соответствуют
соответствуют  , то линейная комбинация векторов
, то линейная комбинация векторов 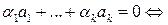 линейная комбинация
линейная комбинация  с теми же коэффициентами
с теми же коэффициентами  равна нулю, т.е.
равна нулю, т.е.  .
. –мерных линейных пространства V и
–мерных линейных пространства V и 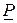 изоморфны.
изоморфны. − базис
− базис 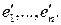 Каждому элементу
Каждому элементу  , поставим в соответствие элемент
, поставим в соответствие элемент  с теми же координатами
с теми же координатами 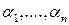 в базисе
в базисе  .
. имеет единственным образом определенные координаты
имеет единственным образом определенные координаты 
 .
. соответствует единственный
соответствует единственный  . Легко видеть, что если
. Легко видеть, что если  в силу введенного соответствия.
в силу введенного соответствия. или
или  . На чертеже направленный отрезок снабжен стрелкой на конце(см. рис.1)
. На чертеже направленный отрезок снабжен стрелкой на конце(см. рис.1) направленного отрезка
направленного отрезка 
 называются сонаправленными (обозначается
называются сонаправленными (обозначается  ), если они лежат на параллельных прямых и направлены в одну сторону.
), если они лежат на параллельных прямых и направлены в одну сторону. ), если они лежат на параллельных прямых и направлены в разные стороны.
), если они лежат на параллельных прямых и направлены в разные стороны.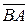 называются противоположными.
называются противоположными. и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено.
и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено. ).
). , то
, то  ,
,  .
. называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором
называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором  ; Его длина равна нулю, а направление не определено.
; Его длина равна нулю, а направление не определено. .
. и
и 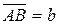 . Тогда
. Тогда  есть направленный отрезок и значит, определяет вектор.
есть направленный отрезок и значит, определяет вектор. . Пусть
. Пусть  ,
,  . Тогда
. Тогда  – параллелограмм; аналогично,
– параллелограмм; аналогично,  – параллелограмм
– параллелограмм 
 – параллелограмм
– параллелограмм  , т.е. они определяют один и тот же вектор.
, т.е. они определяют один и тот же вектор. называется суммой векторов
называется суммой векторов 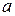 и
и  . Пишут:
. Пишут: 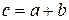 .
. .
. .
. , т.к.
, т.к.  .
. вектор, называемый вектором, противоположным
вектор, называемый вектором, противоположным  . Доказательство свойств может быть проиллюстрировано рис.2
. Доказательство свойств может быть проиллюстрировано рис.2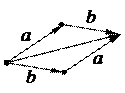
 , то через
, то через  обозначим
обозначим  . Тогда
. Тогда  .
.
 называется вектор
называется вектор  и противоположно направлены, если
и противоположно направлены, если  ;
; .
. .
.


