
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние от точки до плоскости. Расстояние между параллельными плоскостями.
Определение. Будем называть расстоянием от точки до плоскости минимальное расстояние от данной точки до точек m-плоскости. Т.к. минимальное расстояние от данной точки до точек всякой прямой, лежащей на m-плоскости, является расстоянием от данной точки до основания перпендикуляра, опущенного из нее на прямую. Расстояние от точки до m-плоскости равно расстоянию от этой точки до основания перпендикуляра, опущенного из нее на m-плоскость. Найдем расстояние от точки Утверждение. Поскольку у параллельных плоскостей могут быть выбраны одни и те же направляющие векторы Определение. Будем называть число, равно этим расстояниям, расстоянием между двумя параллельными плоскостями. Если уравнения двух плоскостей записаны в виде: 23. Приведение уравнения кривой второго порядка к каноническому виду с классификацией возможных типов типов в случае δ≠0 Зафиксируем на плоскости прямоугольную систему координат и рассмотрим общее уравнение второй степени. (1) Def: Множество точек, координаты которых удовлетворяют уравнению 1 называют кривой второго порядка. Группу старших членов (2)
Положим (11) Значит Разделим случаи: 1)
(13) А) Предположим, что, то есть все λ одного знака, тогда геометрическое место точек координаты которых удовлетворяют условию 13 представляет собой: a. Эллипс, если знак с противоположен знаку λ b. «Мнимый эллипс», если знак с=знаку λ c. точку, если с=0 В) Пусть a. уравнением гиперболы: b. И пары пересекающихся прямых, если c=0
3) Пусть a. пары параллельных прямых, если сλ2<0 b. совпадающих прямых, если с=0 c. «мнимых параллельных прямых», если cλ2>0
Def: Инвариантой кривой называются функции коэффициентов уравнения кривой, которые не меняются при переходе от одной прямоугольной системы координат к другой. Теорема. Для кривой второго порядка
В случае, когда все λi отличны от нуля. Поверхность, путем преобразования квадратичной формы с помощью матрицы перехода Р (как в кривых только для матрицы 3х3) и затем преобразования координат и приведения их к каноническому виду, преобразуется в следующий вид:
27. Приведение уравнения поверхности второго порядка к каноническому виду с классификацией типов в случае, когда одно из λi равно нулю. Пусть, для определенности, λ3=0. Тогда уравнение поверхности примет вид:
28. Приведение уравнения поверхности второго порядка к каноническому виду с классификацией типов в случае, когда два из λi равны нулю. Пусть Если a2 ≠ 0 или a3≠0, делаем замену, полагая:
Теорема 1: Пространство R можно разложить в прямую сумму инвариантных подпространств N0(p) и M(p). При этом подпространство N0(p) состоит только их собственных и присоединенных векторов, отвечающих собственному значению λ=0, а в подпространстве M(p) преобразование обратимо (т.е. λ=0 не является собственным значением преобразования A в подпространстве M(p). Доказательство: для доказательства первого утверждения нам достаточно показать, что пересечение подпространств N0(p) и M0(p) равно нулю. Допустим противное, т.е пусть существует вектор y≠0 такой, что yÎM(p) и yÎN0(p). Так как yÎM(p), то y=Apx. Далее, так как yÎN0(p), то Apy=0 Но из равенств (8) и (9) следует, что существует такой вектор x, для которого Apx≠0 и в то же время A2px = Apy = 0 Это значит, что x есть присоединенный вектор преобразования A с собственным значением λ=0, не принадлежащий подпространству N0(p) , что невозможно, так как N0(p) состоит из всех таких векторов.
Таким образом мы доказали, что пересечение N0(p) и M0(p) равно нулю. Так как сумма размерностей этих подпространств равна n (это ядро и образ преобразования Ap), то отсюда следует, что пространство R раскладывается в прямую сумму этих подпространств: R = M(p) Докажем теперь второе утверждение теоремы, т.е. что в подпространстве M(p) преобразование A не имеет нулевого собственного значения. Действительно, если бы это было не так, то в M(p) существовал бы вектор x≠0 такой, что Apx=0 Но это равенство означает, что xÎN0(p), т.е. является общим вектором M(p) и N0(p), а мы доказали, что таким вектором может быть только нуль. Теорема 2: Пусть преобразование A пространства R имеет k различных собственных значений λ1,….,λk. Тогда R можно разложить в прямую сумму k инвариантных подпространств Nλ1(p1),….,Nλk(pk): R = Nλ1(p1) Каждое из подпространств Nλi(pi) состоит только из собственных и присоединенных векторов, отвечающих собственному значению λi Другими словами, для каждого i существует такое число pi, что для всех xÎNλi(pi): (A-λiI) pi x = 0
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.59 (0.037 с.) |
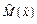 до плоскости, заданной уравнением
до плоскости, заданной уравнением 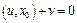 (4). Уравнение перпендикуляра, опущенного из точки
(4). Уравнение перпендикуляра, опущенного из точки 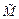 на плоскость имеет вид:
на плоскость имеет вид: 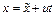 (12). Подставим (12) в (4):
(12). Подставим (12) в (4): 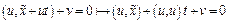 .
. 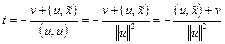 (13). Т.к. расстояние
(13). Т.к. расстояние 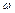 от точки
от точки 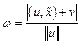 (14). В частности расстояние до плоскости от начала системы равно
(14). В частности расстояние до плоскости от начала системы равно 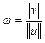 (15). Когда вектор нормали единичный, формулу (14) можно записать, как
(15). Когда вектор нормали единичный, формулу (14) можно записать, как 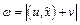 (14’), а (15):
(14’), а (15): 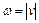 (15’). В случае, когда вектор нормали единичный, абсолютная величина свободного члена в (4) равна расстоянию до плоскости.
(15’). В случае, когда вектор нормали единичный, абсолютная величина свободного члена в (4) равна расстоянию до плоскости.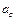 , то векторы нормали параллельных плоскостей коллинеарны. Расстояния от всех точек одной из двух параллельных плоскостей до другой из этих плоскостей равны. Действительно, расстояние от произвольной точки
, то векторы нормали параллельных плоскостей коллинеарны. Расстояния от всех точек одной из двух параллельных плоскостей до другой из этих плоскостей равны. Действительно, расстояние от произвольной точки 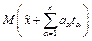 к плоскости, проведенной через точку
к плоскости, проведенной через точку 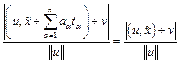 . Т.е. равно расстоянию
. Т.е. равно расстоянию 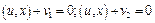 (17), то расстояние между ними равно расстоянию от точки
(17), то расстояние между ними равно расстоянию от точки  , но т.к. точка
, но т.к. точка 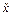 удовлетворяет уравнению этой плоскости, т.е.
удовлетворяет уравнению этой плоскости, т.е. 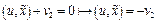 . Получаем:
. Получаем: 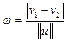 (18).
(18).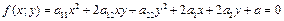
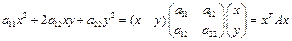 можно рассматривать как квадратичную форму от координат (х,у) вектора х. Поскольку матрица А-симметрична, то ортонормированный базис
можно рассматривать как квадратичную форму от координат (х,у) вектора х. Поскольку матрица А-симметрична, то ортонормированный базис 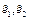 из собственных векторов а, в котором матрица квадратичной формы диагональна и вещественна. Пусть матрица P=[pij] – матрица перехода от базиса е к базису
из собственных векторов а, в котором матрица квадратичной формы диагональна и вещественна. Пусть матрица P=[pij] – матрица перехода от базиса е к базису 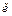 . Тогда
. Тогда 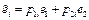 . Тогда (5)
. Тогда (5) 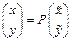 . С учетом 5 запишем квадратичную форму 2. (6)
. С учетом 5 запишем квадратичную форму 2. (6) 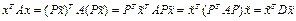 Причем
Причем 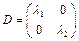 (легко выводится умножением PTAP). Следовательно в базисе
(легко выводится умножением PTAP). Следовательно в базисе 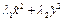 . Поскольку PTP=I, матрица Р – ортогональная и геометрически переходу от базиса к базису соответствует поворот на некоторый у
. Поскольку PTP=I, матрица Р – ортогональная и геометрически переходу от базиса к базису соответствует поворот на некоторый у 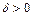 гол φ против часовой стрелки.
гол φ против часовой стрелки. 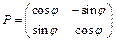 . В силу справедливости 5,6 перепишем уравнение 1 в новых координатах. (10)
. В силу справедливости 5,6 перепишем уравнение 1 в новых координатах. (10) 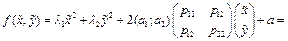
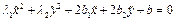
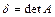 . Тогда λ1λ2 =detD=det(PTAP)=detPT detA detP=detA.
. Тогда λ1λ2 =detD=det(PTAP)=detPT detA detP=detA.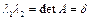
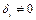
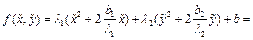
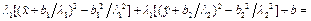
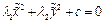 . Причем:
. Причем: 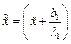 ,
, 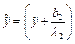 ,
, 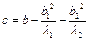 .
.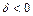 , т.е. λ1 и λ2 разных знаков. Тогда 13 будет
, т.е. λ1 и λ2 разных знаков. Тогда 13 будет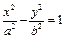 , если c≠0
, если c≠0 . Будем для определенности считать, что λ1=0, а λ2≠0. Тогда уравнение 10 преобразуется к виду:
. Будем для определенности считать, что λ1=0, а λ2≠0. Тогда уравнение 10 преобразуется к виду: 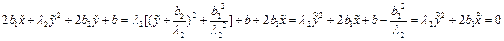 . Полученное уравнение – уравнение параболы. Если же b1=0, то уравнение приводится к следующему виду:
. Полученное уравнение – уравнение параболы. Если же b1=0, то уравнение приводится к следующему виду: 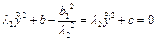 . Это уравнение:
. Это уравнение: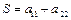 ,
, 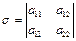 ,
, 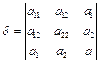 являются инвариантами. В доказательстве рассматривается 2 случая: 1) параллельный перенос (производится замена переменных, открываются скобки, группируется) 2) Поворот с использованием Р.(с помощью Р приводится к диагональной D=PTAP, а затем вычисляются инварианты от D)
являются инвариантами. В доказательстве рассматривается 2 случая: 1) параллельный перенос (производится замена переменных, открываются скобки, группируется) 2) Поворот с использованием Р.(с помощью Р приводится к диагональной D=PTAP, а затем вычисляются инварианты от D)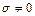
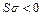 - Эллипс
- Эллипс
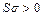 - Эллипс
- Эллипс
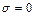
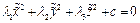 . Тогда имеем следующее.
. Тогда имеем следующее.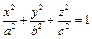
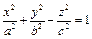
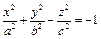
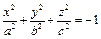
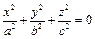
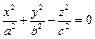
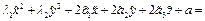
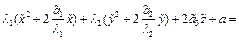
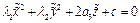 (4). Если в 4
(4). Если в 4 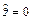 , то уравнение становится уравнением цилиндрической поверхности.
, то уравнение становится уравнением цилиндрической поверхности. 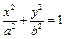
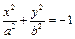
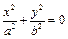
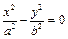
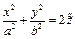
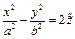
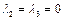 , тогда уравнение поверхности примет вид:
, тогда уравнение поверхности примет вид: 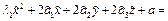
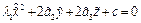 (7). Это пара параллельных плоскостей, различных, когда λ1C<0, совпадающих, когда C=0, мнимых, если λ1C>0.
(7). Это пара параллельных плоскостей, различных, когда λ1C<0, совпадающих, когда C=0, мнимых, если λ1C>0.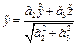 ,
, 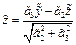 . Подставляя в 7 получаем:
. Подставляя в 7 получаем: 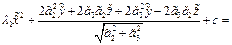
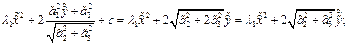 , где
, где 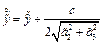 . Это кривая второго порядка на плоскости или параболический цилиндр.
. Это кривая второго порядка на плоскости или параболический цилиндр.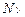 (p1) +
(p1) + 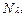 (p2) + … +
(p2) + … + 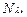 (pk)
(pk) 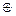 N0(p)
N0(p)


