Определение. Пусть даны квадратичная матрица А размерностью  и функция
и функция  скалярного аргумента
скалярного аргумента  . Распространим
. Распространим  на матричное значение аргумента. Если
на матричное значение аргумента. Если  , то функция от матрицы приобретает вид
, то функция от матрицы приобретает вид  .
.
Теорема Гамильтона. Пусть  - минимальный многочлен. Разложим его на множители
- минимальный многочлен. Разложим его на множители 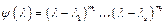 (1), где
(1), где  - все различные собственные значения матрицы А. Степень же
- все различные собственные значения матрицы А. Степень же 
 чисел
чисел  (2) будем называть значениями функции
(2) будем называть значениями функции  на спектре матрицы А. Очевидно, чтобы значения функции
на спектре матрицы А. Очевидно, чтобы значения функции  на спектре матрицы А полностью определяют
на спектре матрицы А полностью определяют  , т.е. все функции
, т.е. все функции  , имеющие одни и те же значения на спектре матрицы А имели одно и то же матричное значение
, имеющие одни и те же значения на спектре матрицы А имели одно и то же матричное значение  . Т.о. для определения
. Т.о. для определения  в общем случае достаточно найти многочлен
в общем случае достаточно найти многочлен  , который принимал бы те же значения на спектре матрицы А, что и
, который принимал бы те же значения на спектре матрицы А, что и  , и положить, что
, и положить, что  .
.
Определение. Если функция  определена на спектре матрицы А, то
определена на спектре матрицы А, то  , где
, где  - любой многочлен, принимающий на спектре те же значения, что и
- любой многочлен, принимающий на спектре те же значения, что и  , т.е.
, т.е.  .Среди всех многочленов с комплексными коэффициентами, принимающих те же значения на спектре, что и
.Среди всех многочленов с комплексными коэффициентами, принимающих те же значения на спектре, что и  , существует единственный многочлен
, существует единственный многочлен  , степень которого меньше m. Этот многочлен однозначно определяется интерполирующими условиями:
, степень которого меньше m. Этот многочлен однозначно определяется интерполирующими условиями:
 (3) – интерполяционный многочлен Лагранжа-Сильвестра.
(3) – интерполяционный многочлен Лагранжа-Сильвестра.
Определение. Пусть функция  , определена на спектре матрицы А, а
, определена на спектре матрицы А, а  - соответствующий интерполяционный многочлен. Тогда
- соответствующий интерполяционный многочлен. Тогда  .
.
Замечание. Получили, что если  матрицы А не имеет кратных корней (матрица простой структуры) и в равенстве (1)
матрицы А не имеет кратных корней (матрица простой структуры) и в равенстве (1)  , то для того, чтобы
, то для того, чтобы  имело смысл достаточно, чтобы
имело смысл достаточно, чтобы  была определена в точках
была определена в точках  , если же все
, если же все  имеют кратные корни, то в некоторых точках соотношения (2) должны быть определены и производные до известного порядка.
имеют кратные корни, то в некоторых точках соотношения (2) должны быть определены и производные до известного порядка.
Свойства функций от матриц:
1) Если  - собственные числа матрицы А n-ого порядка, то
- собственные числа матрицы А n-ого порядка, то  - собственные числа матрицы
- собственные числа матрицы  .
.
2) Если матрицы А и В подобны, т.е.  , то матрицы
, то матрицы  и
и  также подобны, причем
также подобны, причем  .
.
Доказательство. Пусть  . Покажем, что
. Покажем, что  , используя метод математической индукции. Для k=1, это очевидно. Пусть это верно и для k=m. Докажем, что это верно и для k=m+1. Действительно,
, используя метод математической индукции. Для k=1, это очевидно. Пусть это верно и для k=m. Докажем, что это верно и для k=m+1. Действительно,  . Тогда
. Тогда  .
.  .
.
Т.о. две подобные матрицы имеют одинаковые минимальные многочлены и аналогично  принимает одни и те же значение как на спектре матрицы А так и на спектре матрицы В. Поэтому существует интерполяционный многочлен
принимает одни и те же значение как на спектре матрицы А так и на спектре матрицы В. Поэтому существует интерполяционный многочлен 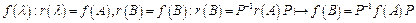 .
.
3) Пусть А – квазидиагональная матрица  , тогда
, тогда  .
.
Доказательство. Обозначим через  интерполяционный многочлен функции
интерполяционный многочлен функции  на спектре матрицы А.
на спектре матрицы А. 
 (5)
(5)  . Минимальный многочлен
. Минимальный многочлен  является аннулирующим многочленом для матрицы
является аннулирующим многочленом для матрицы  , поэтому из равенства
, поэтому из равенства  . Поэтому
. Поэтому  и
и  .
.
Интерполяционный многочлен Лагранжа-Сильвестра. Пусть  - минимальный многочлен матрицы А,
- минимальный многочлен матрицы А,  .
.  - степень
- степень  . Представим
. Представим 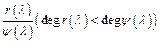 является правильной дробью в виде суммы дробей:
является правильной дробью в виде суммы дробей:  (6), где
(6), где  - некоторые числа. Для определения числителя простой дроби умножим обе части (6) на
- некоторые числа. Для определения числителя простой дроби умножим обе части (6) на  (7), где
(7), где  - рациональная функция, не обращающаяся в бесконечность при
- рациональная функция, не обращающаяся в бесконечность при  . Обозначим через
. Обозначим через  .
.  (8)
(8)
Формулы (8) показывают, что числители 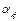 в правой части (6) выражаются через значения многочлена
в правой части (6) выражаются через значения многочлена  на спектре матрицы А, а эти значения нам известны. А именно, они равны соответственным значения функции
на спектре матрицы А, а эти значения нам известны. А именно, они равны соответственным значения функции  и ее производной:
и ее производной:  (9’). После того, как все
(9’). После того, как все 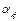 найдены, мы определим
найдены, мы определим  по следующей формуле, которая получается умножением обеих частей равенства (6) на
по следующей формуле, которая получается умножением обеих частей равенства (6) на  :
:  (10). Заметим, что в соотношении (10) выражение в квадратных скобках в силу (9’) равно сумме первых
(10). Заметим, что в соотношении (10) выражение в квадратных скобках в силу (9’) равно сумме первых  членов разложения Тейлора по степеням
членов разложения Тейлора по степеням  для
для  .
.
Основная формула. Вернемся к (10). Подставив в нее (9’) для коэффициентов 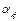 и объединив члены, содержащие одно и тоже значение
и объединив члены, содержащие одно и тоже значение  и какой-либо ее производной, представим
и какой-либо ее производной, представим  в виде
в виде  (11), где
(11), где  - полином
- полином  степени меньшей степени
степени меньшей степени  . Эти полиномы определяются заданием
. Эти полиномы определяются заданием  и не зависит от выбора функции
и не зависит от выбора функции  . Число этих полиномов равно числу значений
. Число этих полиномов равно числу значений  на спектре матрицы А и равно m, где m – степень минимального многочлена. Из формулы (10) следует основная формула для нахождения функции от матрицы, а именно:
на спектре матрицы А и равно m, где m – степень минимального многочлена. Из формулы (10) следует основная формула для нахождения функции от матрицы, а именно:  (12), матрицы
(12), матрицы 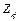 являются компонентами матрицы А. Они вполне определяются заданием матрицы А и не зависят от выбора функции
являются компонентами матрицы А. Они вполне определяются заданием матрицы А и не зависят от выбора функции  . В правой части формулы (12), функция
. В правой части формулы (12), функция  представлена только своими значениями на спектре матрицы А.
представлена только своими значениями на спектре матрицы А.


 и функция
и функция  скалярного аргумента
скалярного аргумента  . Распространим
. Распространим  , то функция от матрицы приобретает вид
, то функция от матрицы приобретает вид  .
. - минимальный многочлен. Разложим его на множители
- минимальный многочлен. Разложим его на множители 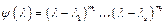 (1), где
(1), где  - все различные собственные значения матрицы А. Степень же
- все различные собственные значения матрицы А. Степень же 
 чисел
чисел  (2) будем называть значениями функции
(2) будем называть значениями функции  , т.е. все функции
, т.е. все функции  , который принимал бы те же значения на спектре матрицы А, что и
, который принимал бы те же значения на спектре матрицы А, что и  .
. .Среди всех многочленов с комплексными коэффициентами, принимающих те же значения на спектре, что и
.Среди всех многочленов с комплексными коэффициентами, принимающих те же значения на спектре, что и  , степень которого меньше m. Этот многочлен однозначно определяется интерполирующими условиями:
, степень которого меньше m. Этот многочлен однозначно определяется интерполирующими условиями: (3) – интерполяционный многочлен Лагранжа-Сильвестра.
(3) – интерполяционный многочлен Лагранжа-Сильвестра. .
. , то для того, чтобы
, то для того, чтобы  , если же все
, если же все  - собственные числа матрицы А n-ого порядка, то
- собственные числа матрицы А n-ого порядка, то  - собственные числа матрицы
- собственные числа матрицы  , то матрицы
, то матрицы  также подобны, причем
также подобны, причем  .
. , используя метод математической индукции. Для k=1, это очевидно. Пусть это верно и для k=m. Докажем, что это верно и для k=m+1. Действительно,
, используя метод математической индукции. Для k=1, это очевидно. Пусть это верно и для k=m. Докажем, что это верно и для k=m+1. Действительно,  . Тогда
. Тогда  .
.  .
.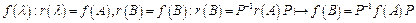 .
. , тогда
, тогда  .
.
 (5)
(5)  . Минимальный многочлен
. Минимальный многочлен  , поэтому из равенства
, поэтому из равенства  . Поэтому
. Поэтому  и
и  .
. .
.  - степень
- степень 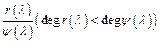 является правильной дробью в виде суммы дробей:
является правильной дробью в виде суммы дробей:  (6), где
(6), где  - некоторые числа. Для определения числителя простой дроби умножим обе части (6) на
- некоторые числа. Для определения числителя простой дроби умножим обе части (6) на  (7), где
(7), где  - рациональная функция, не обращающаяся в бесконечность при
- рациональная функция, не обращающаяся в бесконечность при  . Обозначим через
. Обозначим через  .
.  (8)
(8)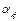 в правой части (6) выражаются через значения многочлена
в правой части (6) выражаются через значения многочлена  (9’). После того, как все
(9’). После того, как все  (10). Заметим, что в соотношении (10) выражение в квадратных скобках в силу (9’) равно сумме первых
(10). Заметим, что в соотношении (10) выражение в квадратных скобках в силу (9’) равно сумме первых  членов разложения Тейлора по степеням
членов разложения Тейлора по степеням  для
для  .
. (11), где
(11), где  - полином
- полином  (12), матрицы
(12), матрицы 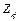 являются компонентами матрицы А. Они вполне определяются заданием матрицы А и не зависят от выбора функции
являются компонентами матрицы А. Они вполне определяются заданием матрицы А и не зависят от выбора функции 


