
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема. Критерий эквивалентности двух матриц.
Для того, чтобы две прямоугольные матрицы одинаковых размеров были эквивалентными ó чтобы они имели один и тот же ранг. Доказательство: -> Ранг произведения двух матриц не превосходит ранга любой из них. При умножении какой-либо матрицы на невырожденную матрицу ранг ее не меняется, поэтому эквивалентные матрицы имеют один и тот же ранг. Можно показать и обратное, что матрицы одинаковых рангов эквивалентны между собой. Мы докажем, что всякая матрица ранга r эквивалентна Ir(единичной матрице размерности r). Пусть дана прямоугольная матрица размера nxm. Она определяет некоторый линейный оператор А, отображающий пространство Х с базисом е в пространство Y с базисом g. Обозначим через r число линейно независимых векторов среди образов векторов базиса Ae1,...,Aen. Не нарушая общности можно считать, что линейно независимыми являются векторы Ae1,...,Aer. Остальные векторы выражаются через них. Определим новый базис следующим образом: Def: А называется подобной матрице B если существует такая невырожденная матрица P, что A=P-1BP. 1) Если А подобна В, то В подобна А. 2)Если А подобна В, а В подобна С, то А подобна С. Поскольку признак подобия удовлетворяет условиям рефлексивности, симметричности и транзитивности, он является отношением эквивалентности. 10. Инвариантные подпространства. Собственные векторы и собственные значения линейного оператора. Доказать, что в комплексном линейном пространстве всякий линейный оператор имеет хотя бы один собственный вектор. Def: Подпространство L линейного пространства X называется инвариантным, относительно А, если для xÎL верно: AxÎL. Всякий линейный оператор имеет по крайней мере 2 тривиальных инвариантных подпространства: 1) Нулевое подпространство 2) Все пространство Х.
Пусть L1 – одномерное подпространство, порожденное ненулевым вектором Х. Ясно, что для того, чтобы L1 было инвариантным ó Ax Î L1. Ax=λx; Def: Вектор х ≠ θ, удовлетворяющий Ax=λx называется собственным вектором, а соответствующее ему число λ - собственным значением. Все отличные от нуля векторы инвариантного подпространства являются собственными. Теорема. В комплексном линейном пространстве Х линейный оператор имеет хотя бы один собственный вектор. Доказательство. Пусть в линейном пространстве Х выбран базис e1,...,en. В этом базисе А соответствует матрица Ае=[aij]. Выберем произвольный х Î Х. х = α1e1+...+ αnen. А координаты β выражаются формулами: 11. Доказать, что а) характеристический многочлен не зависит от выбора базиса; б) система собственных векторов, соответствующих попарно различным собственным значениям, линейно независима; в) собственные векторы линейного оператора, соответствующие одному собственному значению, вместе с нулевым вектором образуют подпространство. Связь между линейными операторами и билинейными формами в унитарном пространстве. Определение. Многочлен, стоящий в левой части уравнения Теорема 2. Характеристический многочлен не зависит от выбора базиса. Доказательство. Зафиксируем в пространстве Х некоторый базис
Теорема 3. Если линейный оператор А имеет n линейно независимых векторов (является оператором простой структуры), то, выбрав их в качестве базиса линейного пространства, мы приведем матрицу линейного оператора к диагональной форме. Обратно, если в некотором базисе матрица линейного оператора диагональна, то все векторы этого базиса являются собственными векторами. Доказательство. Пусть А – линейный оператор, который имеет n линейно независимых векторов, где Теорема 4. Система собственных векторов Доказательство. (через математическую индукцию).
1. n=1. Т.е. 2. Пусть теорема верна для n-1 векторов, т.е. 3. Докажем, что теорема верна для n векторов (от противного): Теорема 5. Если характеристический многочлен линейного оператора А имеет n различных корней, то матрица линейного оператора А может быть приведена к диагональной форме. Доказательство. Каждому корню Теорема 6. Собственные векторы линейного оператора А, соответствующие собственному значению Доказательство. Пусть Утверждение. Всякому линейному оператору А в линейном пространстве с определенным скалярным произведением отвечает билинейная форма Проверка на корректность: 1) 2) Проверка на однозначность:
Утверждение. Каждой билинейной форме в линейном пространстве со скалярным произведением отвечает линейный оператор А такой, что: 12. Операция перехода от оператора A к сопряженному Нахождение матрицы сопряженного оператора в ортонормированном базисе. Пусть в линейном пространстве Х выбран ортонормированный базис
Матрица сопряженного оператора Теорема 1. Формула
Определение. Оператор Свойства операции 1) 2) 3) 4) 5)
|
|||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 973; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.186.164 (0.01 с.) |
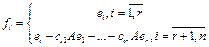 . Тогда, если мы возьмем и рассмотрим образ i-го базисного вектора f, то Afi=θ для i=r+1,n. Векторы h1...hr – линейно независимы, а это векторы из Y. Дополним их некоторыми векторами hr+1,...,hm До базиса в линейном пространстве Y. И рассмотрим матрицу оператора А в новых базисах f1...fn и h1...hm. Коэффициенты i-го столбца этой матрицы совпадает с коэффициентами вектора Afi в базисе h. Согласно соотношениям матрица А будет совпадать с матрицей Ir. Т.к. А и Ir соответствуют одному и тому же оператору, то они эквивалентны.
. Тогда, если мы возьмем и рассмотрим образ i-го базисного вектора f, то Afi=θ для i=r+1,n. Векторы h1...hr – линейно независимы, а это векторы из Y. Дополним их некоторыми векторами hr+1,...,hm До базиса в линейном пространстве Y. И рассмотрим матрицу оператора А в новых базисах f1...fn и h1...hm. Коэффициенты i-го столбца этой матрицы совпадает с коэффициентами вектора Afi в базисе h. Согласно соотношениям матрица А будет совпадать с матрицей Ir. Т.к. А и Ir соответствуют одному и тому же оператору, то они эквивалентны.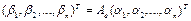 .
. 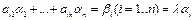 . Переносим и группируем. Для доказательства теоремы нужо показать, что λ и числа α1,...,αn не все равные нулю, удовлетворяющие системе 2. Условием существования ненулевого решения системы 2 является равенство нулю ее определителя. det(A-λI)=0. Мы получили уравнение n-ой степени, относительно λ. Это уравнение имеет хотя бы один корень (в общем случае комплексный) λ0. Подставив в систему 2 вместо λ λ0 получим однородную СЛАУ с нулевым определителем, имеющую ненулевое решение. Тогда вектор х, удовлетворяющий этому решению будет собственным вектором, соответствующим собственному значению λ0.
. Переносим и группируем. Для доказательства теоремы нужо показать, что λ и числа α1,...,αn не все равные нулю, удовлетворяющие системе 2. Условием существования ненулевого решения системы 2 является равенство нулю ее определителя. det(A-λI)=0. Мы получили уравнение n-ой степени, относительно λ. Это уравнение имеет хотя бы один корень (в общем случае комплексный) λ0. Подставив в систему 2 вместо λ λ0 получим однородную СЛАУ с нулевым определителем, имеющую ненулевое решение. Тогда вектор х, удовлетворяющий этому решению будет собственным вектором, соответствующим собственному значению λ0.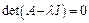 называется характеристическим многочленом матрицы оператора А, а само уравнение называет характеристическим или вековым уравнением этой матрицы.
называется характеристическим многочленом матрицы оператора А, а само уравнение называет характеристическим или вековым уравнением этой матрицы. и обозначим через
и обозначим через 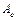 матрицу оператора А в этом базисе. Пусть в некотором базисе
матрицу оператора А в этом базисе. Пусть в некотором базисе  оператор имеет матрицу
оператор имеет матрицу 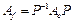 . Тогда
. Тогда 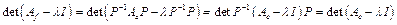 .
.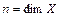 и пусть
и пусть 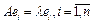 . Выберем
. Выберем  , линейно независима.
, линейно независима.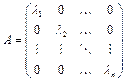
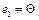 . Теорема верна.
. Теорема верна.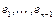 линейно независимы.
линейно независимы.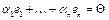 (4) - не все коэффициенты в этой линейной комбинации ненулевые. Пусть
(4) - не все коэффициенты в этой линейной комбинации ненулевые. Пусть 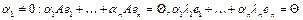 .
. 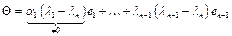 . Имеем нулевую комбинацию линейно независимых векторов, а значит и противоречие.
. Имеем нулевую комбинацию линейно независимых векторов, а значит и противоречие. характеристического уравнения отвечает хотя один собственный вектор. Т.к. у этих собственных векторов собственные значения различны, то по теореме 4 мы имеем n линейно независимых векторов
характеристического уравнения отвечает хотя один собственный вектор. Т.к. у этих собственных векторов собственные значения различны, то по теореме 4 мы имеем n линейно независимых векторов  , вместе с нулевым вектором образуют подпространство пространства Х.
, вместе с нулевым вектором образуют подпространство пространства Х.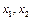 - два собственных вектора линейного оператора А, соответствующие одному собственному значению
- два собственных вектора линейного оператора А, соответствующие одному собственному значению 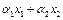 - тоже собственный вектор:
- тоже собственный вектор: 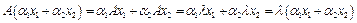 . Указанное подпространство, порожденное собственным значение, является ядром оператора
. Указанное подпространство, порожденное собственным значение, является ядром оператора 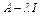 .
. , задаваемая соотношением:
, задаваемая соотношением: 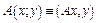 .
.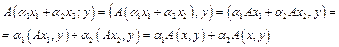
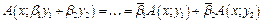 .
.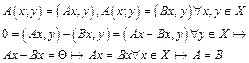
 .
. . Свойства операции
. Свойства операции 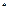 . Нахождение матрицы сопряженного оператора в ортонормированном (ортогональном) базисе.
. Нахождение матрицы сопряженного оператора в ортонормированном (ортогональном) базисе.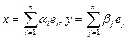 .
.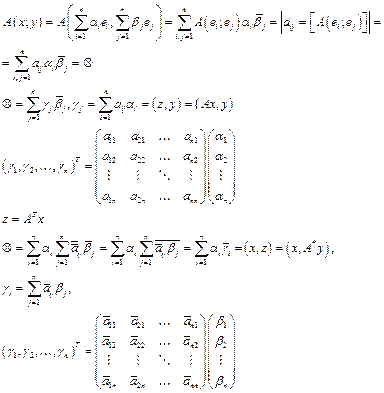
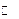
 . При этом матрица линейного оператора
. При этом матрица линейного оператора 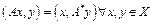 .
.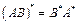 ;
;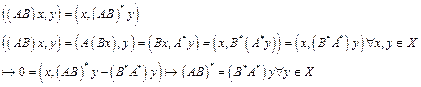
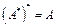 ;
;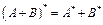 ;
;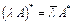 ;
;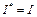 .
.


