
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон инерции квадратичной формы. Ранг квадратичной формы.Содержание книги
Поиск на нашем сайте
Теорема. Если квадратичная форма приведена двумя различными способами (в двух различных базисах) к сумме квадратов, то число положительных, отрицательных и нулевых коэффициентов в обоих случая одно и то же. Доказательство. Пусть в базисе Определение. Число r, отличных от нуля коэффициентов Чтобы найти ранг квадратичной формы нужно вычислить ранг ее матрицы в какой-либо одной системе координат. Определение. Назовем число положительных Определение. Если 6. Определение и примеры линейных операторов. Действия с линейными операторами. Пространство линейных операторов. Определение. Пусть Х и У – линейные пространства, заданные на одним и тем же полем F. Правило, по которому каждому элементу Определение. Запись Определение. Образ оператора А или область его значений это совокупность всех элементов Определение. Оператор А с областью определения Х и областью значений У называется линейным оператором, если он линейной комбинацией прообразов ставит в соответствие линейную комбинацию образов. Определение. Если Определение. Операторы А и В называются равными (А=В) тогда и только тогда, когда Определение. Суммой операторов А и В называется оператор С=А+В, если Если
Эта операция коммутативна и ассоциативна: 1) 2) В 3) 4) Введем операцию умножения оператора на число: Определение. Рассмотрим пространства Х, У и Z, заданные над одним и тем же полем F. Пусть
Свойства: 5) 6) 7) 8) 9) 7. Ядро и образ линейного оператора. Связь между дефектом, рангом и размерностью области определения линейного оператора. Обратный оператор. Невырожденный оператор. Def: Оператор I Î WXX называется тождественным (единичным) Оператором, если Ix=x; хÎХ. Def: Оператор B Î WXX называется обратным к А, если AB=BA=I (B=A-1). Любой линейный оператор переводит θ->θ. Def: R(A) ={y|y=Ax,xÎX}– образ А - подмножество Y, замкнутое относительно операций -> подпространство. Def: Ранг оператора rgA = dimR(A) Def: Множество всех х, для которых Ах=θ называется ядром оператора А. N(A)={x|xÎХ, Ax=θ}. Ядро есть подпространство в Х. Def: Размерность ядра называется дефектом nA=dimN(A). Рассмотрим соотношение между rgA и nA линейного оператора. Пусть А:X->Y. Разложим линейное пространство Х в прямую сумму N(A) + MA, где MA-любое дополнительное подпространство. Значит для х Î Х справедливо единственное представление вида: x=xn+xm. xn из ядра, xm из доп. подпространства. Тогда y = Ax=A(xn+xm)=Axn+Axm=Axm. То есть любой вектор из R(A) имеет хотя бы один прообраз из MA. На самом деле он единственен. (Доказательство от противного (наличия у двух прообразов). Таким образом мы установили взаимоднозначное соответствие между MA и R(A). Можно доказать, что оно является изоморфизмом. dimX=dimN(A)+dimMA=nA-rgA Def: Линейный оператор А:Х->X называется невырожденным, если его ядро состоит только из θ, в противном случае – оператор вырожденный. 8. Определение и примеры нахождения матриц линейных операторов. Связь между координатами вектора – образа и вектора – прообраза. Изоморфизм пространства линейных операторов пространству прямоугольных матриц соответствующего размера. Определение. Пусть дан линейный оператор А:Х->Y, dimX=n. И некоторым базисом Х является e1,...,en. dimY=m; g1,...,gm – базис Y. x=α1e1+...+αnen. Ax= α1Ae1+...+αnAen. Другими словами, лиейный оператор полностью определяется совокупностью образов Aei базисных векторов е. y Î L(Ae1,...,Aen). Aej – вектор, содержащийся в Y и значит его можно разложить по базису Y. (*) Aej=a1jg1+...+anjgn. Коэффициенты aij определяют некоторую матрицу, в которой n строчек и n столбцов. Эту матрицу назовем матрицей А в базисах e1,...,en g1,...,gn. Столбцами матрицы оператора служат координаты векторов Ае1,...,Аеn в базисе g. Для того, чтобы определить элемент aij нужно найти образ Aej и взять его i-ую координату.
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 квадратичная форма
квадратичная форма  имеет вид:
имеет вид:  (1), где
(1), где  - координаты вектора х, т.е.
- координаты вектора х, т.е.  . Пусть в базисе
. Пусть в базисе  эта квадратичная форма имеет вид:
эта квадратичная форма имеет вид: 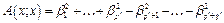 (2), где
(2), где  - координаты вектора х в базисе
- координаты вектора х в базисе  . Докажем это от противного. Предположим, что
. Докажем это от противного. Предположим, что  . Рассмотрим подпространство
. Рассмотрим подпространство 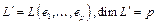 ,
,  . Т.к.
. Т.к.  , то существует ненулевой вектор х, принадлежащий пересечению:
, то существует ненулевой вектор х, принадлежащий пересечению:  . Тогда
. Тогда  . В базисе е вектор х имеет координаты
. В базисе е вектор х имеет координаты  , а в базисе f -
, а в базисе f -  . Подставляя эти представления в формулы (1, 2), мы получаем с одной стороны, что
. Подставляя эти представления в формулы (1, 2), мы получаем с одной стороны, что  (т.к. не все числа
(т.к. не все числа  (Т.к. хотя среди чисел
(Т.к. хотя среди чисел  есть отличные от нуля, возможно, что
есть отличные от нуля, возможно, что  ). Противоречие, следовательно, неравенство
). Противоречие, следовательно, неравенство  .
. в каноническом виде квадратичной формы называется рангом квадратичной формы.
в каноническом виде квадратичной формы называется рангом квадратичной формы. и число отрицательных
и число отрицательных  коэффициентов в каноническом виде квадратичной формы соответственно положительными и отрицательными индексами инерции:
коэффициентов в каноническом виде квадратичной формы соответственно положительными и отрицательными индексами инерции:  .
. , то квадратичная форма называется невырожденной. Разность между положительными и отрицательными индексами инерции называется сигнатурой.
, то квадратичная форма называется невырожденной. Разность между положительными и отрицательными индексами инерции называется сигнатурой. ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  , называется оператором или преобразованием. Результат применения оператора
, называется оператором или преобразованием. Результат применения оператора  обозначают
обозначают  .
. значит, что оператор А действует из Х в У или отображает Х в У. При этом Х называется областью определения оператора А, у – образом элемента х, а х – прообраз у.
значит, что оператор А действует из Х в У или отображает Х в У. При этом Х называется областью определения оператора А, у – образом элемента х, а х – прообраз у. .
. .
. , то линейный оператор называется оператором в Х.
, то линейный оператор называется оператором в Х. .
. (1).
(1). .
. 

 ;
; .
. существует нулевой элемент, который каждому
существует нулевой элемент, который каждому  . Рассмотрим:
. Рассмотрим: ;
;
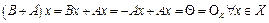
 (2). Покажем, что оператор С линейный.
(2). Покажем, что оператор С линейный. называется произведением оператора В на А:
называется произведением оператора В на А:  . Если
. Если  (3). Произведение линейных операторов также является линейным оператором:
(3). Произведение линейных операторов также является линейным оператором: .
. ;
; ;
; ;
; ;
; .
.


