
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства самосопряженных операторов.
Определение. Линейный оператор А называется самосопряженным или эрмитовым, если Утверждения. 1) Для того, чтобы линейный оператор А был эрмитовым необходимо и достаточно, чтобы соответствующая ему билинейная форма была эрмитовой: 2) Всякий линейный оператор А может быть записан в виде Замечание. Пусть А и В – самосопряженные линейные операторы. Для того, чтобы оператор АВ был самосопряженным необходимо и достаточно, чтобы АВ=ВА, т.е. чтобы линейные операторы А и В были перестановочными. Лемма 1. Собственные значения самосопряженного линейного оператора вещественные. Доказательство. Пусть х – собственный вектор линейного оператора А и
Лемма 2. Доказательство. Х, как ортогональное дополнение к Теорема 1. Для любого самосопряженного линейного оператора в n-мерном унитарном пространстве существует n попарно ортогональных собственных векторов, соответствующие им собственные значения вещественны. Доказательство. В Х существует хотя бы собственный вектор Теорема 2. А – самосопряженный линейный оператор в n-мерном унитарном пространстве, тогда существует ортогональный базис, в котором матрица линейного оператора А диагональна и вещественно. Верно и обратное. Доказательство. Необходимость. Выберем в качестве базиса построенные при доказательстве теоремы 1 собственные векторы Достаточность. Пусть матрица оператора А в ортонормированном базисе имеет вид (1). Итак, в ортонормированном базисе матрица
Теорема 3. Собственные векторы самосопряженного оператора, соответствующие различным собственным значениям, взаимно ортогональны. Доказательство. Пусть у линейного оператора А имеются
Определение. Матрица Теорема 4. Для того, чтобы линейный оператор А был самосопряженным необходимо и достаточно, чтобы его матрица была эрмитовой. Теорема 5. Пусть в n-мерном унитарном пространстве Х задана эрмитова билинейная форма. Тогда в Х существует ортонормированный базис, в котором соответствующая билинейная квадратичная форма, записывается в виде: Доказательство. Пусть
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.6 (0.005 с.) |
 .
.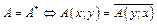 .
. ;
;
 .
.
 - его собственное значение:
- его собственное значение:
 – самосопряженный линейный оператор, а е – его собственный вектор. Тогда совокупность
– самосопряженный линейный оператор, а е – его собственный вектор. Тогда совокупность  есть (n-1)-мерное подпространство, инвариантное относительно линейного оператора А.
есть (n-1)-мерное подпространство, инвариантное относительно линейного оператора А. есть (n-1)-мерное подпространство в Х. Покажем, что это подпространство инвариантно относительно оператора А:
есть (n-1)-мерное подпространство в Х. Покажем, что это подпространство инвариантно относительно оператора А: 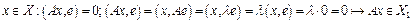 .
. линейного оператора А. По лемме 2 совокупность векторов ортогональных
линейного оператора А. По лемме 2 совокупность векторов ортогональных  . Будем рассматривать линейный оператор
. Будем рассматривать линейный оператор  . Продолжая этот процесс, мы получим в результате n попарно ортогональных собственных векторов
. Продолжая этот процесс, мы получим в результате n попарно ортогональных собственных векторов  . Согласно лемме 1, соответствующие собственные значения вещественны.
. Согласно лемме 1, соответствующие собственные значения вещественны. и пронормируем их. В этом базисе матрица оператора имеет вид:
и пронормируем их. В этом базисе матрица оператора имеет вид:  (1).
(1). получается из матрицы линейного оператора А транспонированием и заменой каждого элемента комплексным сопряжением. Проделав эти операции над матрицей вида (1), где все
получается из матрицы линейного оператора А транспонированием и заменой каждого элемента комплексным сопряжением. Проделав эти операции над матрицей вида (1), где все  - вещественные, мы получим ту же матрицу, следовательно А и
- вещественные, мы получим ту же матрицу, следовательно А и  .
.

 называется эрмитовой, если
называется эрмитовой, если  .
. - координаты Х.
- координаты Х. - эрмитова билинейная форма, т.е.
- эрмитова билинейная форма, т.е.  . Тогда существует самосопряженный линейный оператор А такой, что
. Тогда существует самосопряженный линейный оператор А такой, что  . Выберем в качестве базиса Х ортонормированную систему собственных векторов самосопряженного линейного оператора А (по теореме 1). Тогда
. Выберем в качестве базиса Х ортонормированную систему собственных векторов самосопряженного линейного оператора А (по теореме 1). Тогда  .
. .
.


