Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства симметричных операторов.
Определение. Самосопряженный оператор в евклидовом пространстве называется симметричным, если Утверждение. Пусть Лемма 1. Для всякого симметричного оператора существует одномерное инвариантное пространство. Доказательство. Из теоремы 1 (билет 16) следует, что нам нужно доказать существование вещественного корня
Лемма 2. Пусть А – симметричный оператор, а е – его собственный вектор, тогда множество векторов, ортогональных е, образуют (n-1)-мерное инвариантное пространство: Доказательство. Пусть Теорема 2. Существует ортонормированный базис, в котором матрица симметричного оператора А диагональна. Доказательство. По лемме 1 линейный оператор А имеет хотя бы один собственный вектор, т.к. Теорема 3. Пусть Доказательство.
Определение. Линейный оператор Свойства. 1) ортогональный оператор сохраняет длины векторов; 2) ортогональный оператор сохраняет углы между векторами. 3) Если 4) Матрица 5) Определитель матрицы ортонормированного оператора равен 6) Ортогональный оператор всегда не вырожден. 7) Тождественный оператор является ортогональным. 8) Произведение ортогональных операторов снова будет ортогональным оператором.
9) Оператор, обратный ортогональному, тоже ортогональный. 10) Линейный оператор, переводящий хотя бы один базис в ортонормированный, является ортогональным. Определение. Ортогональные операторы, определитель матрицы которых равен 1, называются собственными, у которых равен –1, несобственными. Лемма 3. Если Доказательство. Если взять Теорема 4. Матрица ортогонального оператора в некотором ортонормированном базисе имеет вид:
Доказательство. По теореме 1 (билет 16) любой линейный оператор в n-мерном евклидовом пространстве имеет одномерное или двумерное инвариантное подпространство
19. Определение аффинного пространства. Различные способы задания прямой в аффинном пространстве (векторный, в параметрическом виде, канонический, по двум точкам). Угол между прямыми. Нахождение расстояния от данной точки до данной прямой. Перпендикуляр, опущенный из точки на прямую.
Def: пусть задано n-мерное векторное пространство Vn над полем F и непустое множество An, элементы которого будем называть точками. Предположим, что упорядоченной паре точек M,N Î An поставлен в соответствие вектор пространства Vn, обозначаемый 1)Для M Î An и a Î Vn единственная точка N Î An, что Тогда множество An называется n-мерным аффинным пространством, связанным с векторным пространством Vn. Способы задания прямой: Def: Будем называть прямой в аффинном пространстве множество точек этого пространства, получаемых из одной его точки всеми переносам, векторы которых коллинеарны. Т.к. векторы этих переносов имеют вид at, где t Î R, радиус-векторы прямой имеют вид (1) x=x0+at. 1) Уравнение 1 называется векторным уравнением прямой. При этом а – направляющий вектор. Две различные прямые, полученные из различных точек одними и теми же переносами, называются параллельными. 2) Координатные уравнения прямой. Уравнение 1 равносильно n координатным уравнениям (2) xi=x0+ait. Уравнение 2 – параметрическое уравнение прямой. Разрешая его относительно T и приравнивая полученные выражения получаем: 3) Уравнение прямой по двум точкам. Если задано две точки M0(x0) и M1(x1), то за направляющий вектор прямой, проходящей через эти две точки можно принять Расстояние от точки до прямой. Расстояние w от точки M(r) до произвольной точки прямой определяется соотношением (7): Перпендикуляр, опущенный из точки на прямую. Требуя, чтобы отрезок MN, соединяющий М(х) с некоторой точкой N прямой, был перпендикулярен направляющему вектору а этой прямой, т.е. чтобы вектор x-x0-at был ортогонален а. (x-x0-at,a)=0. Значение t, удовлетворяющее этому условию совпадает с 8. Это совпадение |-> основание N перпендикуляра, опущенного из данной точки М на прямую, совпадает с той точкой прямой, которая находится на минимальном расстоянии от данной точки. 20. Взаимное расположение двух прямых. Нахождение кратчайшего расстояния между двумя скрещивающимися прямыми. Общий перпендикуляр двух прямых. Взаимное расположение двух прямых. Если две прямые в n-мерном аффинном пространстве, определяющиеся уравнениями
Кратчайшее расстояние между двумя скрещивающимися прямыми. Найдем кратчайшее расстояние между двумя скрещивающимися прямыми l и m, которые записаны уравнением (10):
Вектор MN имеет вид: Вычислим теперь 21. Различные способы задания плоскостей (векторный, в параметрическом виде, по точке и нормали, по точке и направляющим векторам, по n точкам). Основная теорема о плоскости. Угол между плоскостями. Условие принадлежности n+1 точки одной плоскости. Определение. Будем называть m-мерной плоскостью аффинного пространства или m-плоскостью множество всех точек этого пространства, полученных из одной его точки всеми переносами, векторы которых коллинеарны и принадлежат одному линейному пространству. Т.к. векторы этих переносов имеют вида Замечание. Прямые можно рассматривать, как 1-плоскость; точки – как 0-плоскость. Определение. Различные плоскости, получающиеся из различных точек одними и теми же переносами, называются параллельными плоскостями. ( Уравнение (1) равносильно Если задано m+1 точек Определение. Будем называть m-плоскость, определяемую точками Определение. Если m=n-1, то такая плоскость называется гиперплоскостью или просто плоскостью. Если мы умножим обе части уравнения (1) на вектор u, перпендикулярный всем Определение. Вектор u ортогональный ко всем направляющим векторам
Пусть Уравнение плоскости по точке и вектору нормали. Если задана точка Уравнение плоскости по точке и направляющим векторам. Если задана точка Уравнение плоскости по n точкам. Пусть даны n точек Теорема. Если заданы n+1 точек Доказательство. Необходимость. Если точки Достаточность. Если эти векторы линейно зависимы, то существует вектор u, перпендикулярный всем этим векторам, и все эти точки Определение. Углом между двумя плоскостями называется тот из углов между векторами нормали этих плоскостей, который
|
||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.44.223 (0.028 с.) |
 .
. - ортонормированный базис,
- ортонормированный базис,  . Пусть х и у в базисе е имеют координаты:
. Пусть х и у в базисе е имеют координаты:  . Тогда
. Тогда 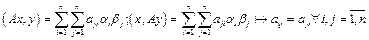 . Это утверждение верно только в ортонормированном базисе.
. Это утверждение верно только в ортонормированном базисе. характеристического уравнения
характеристического уравнения 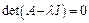 (2). Предположим, что
(2). Предположим, что  . Построим два вектор х и у такие, что
. Построим два вектор х и у такие, что  .
.
 .
. .
. - инвариантное относительно линейного оператора А пространство, то в
- инвариантное относительно линейного оператора А пространство, то в  … В итоге мы получим n собственных векторов, ортогональных по построению. Затем пронормируем их.
… В итоге мы получим n собственных векторов, ортогональных по построению. Затем пронормируем их. - квадратичная форма в n-мерном евклидовом пространстве, тогда существует ортонормированный базис
- квадратичная форма в n-мерном евклидовом пространстве, тогда существует ортонормированный базис  , где
, где  - собственные значения симметричного оператора.
- собственные значения симметричного оператора. . Выберем ортонормированный базис е из собственных векторов (существует по теореме 2).
. Выберем ортонормированный базис е из собственных векторов (существует по теореме 2).
 , действующий в n-мерном евклидовом пространстве Х, называется ортогональным, если он сохраняет скалярное произведение
, действующий в n-мерном евклидовом пространстве Х, называется ортогональным, если он сохраняет скалярное произведение  .
.
 тоже образуют ортонормированный базис в Х.
тоже образуют ортонормированный базис в Х.
 ортогонального оператора в ортонормированном базисе имеет ортонормированные строки и столбцы.
ортогонального оператора в ортонормированном базисе имеет ортонормированные строки и столбцы. .
. .
.
 .
.
 также является инвариантным пространством.
также является инвариантным пространством. . Поскольку А – ортогональный оператор, он не вырожден и его образ на любом инвариантном подпространстве совпадает с этим пространством, поэтому х имеет свой прообраз
. Поскольку А – ортогональный оператор, он не вырожден и его образ на любом инвариантном подпространстве совпадает с этим пространством, поэтому х имеет свой прообраз  .
.
 . Если же
. Если же  . По лемме 3, ортогональное дополнение
. По лемме 3, ортогональное дополнение  соответствуют двумерным инвариантным пространствам.
соответствуют двумерным инвариантным пространствам. , причем выполнены следующие аксиомы:
, причем выполнены следующие аксиомы: .
. - каноническое уравнение прямой.
- каноническое уравнение прямой. =x1-x0 . Поэтому векторное уравнение этой прямой может быть записано в виде x=x0+(x1-x0)t, а каноническое уравнение:
=x1-x0 . Поэтому векторное уравнение этой прямой может быть записано в виде x=x0+(x1-x0)t, а каноническое уравнение: 
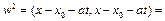

 . Исследуя w2 как функцию от t. (8)
. Исследуя w2 как функцию от t. (8)  - это значение даст минимальное расстояние. Подставляя 8 в 7 получаем:
- это значение даст минимальное расстояние. Подставляя 8 в 7 получаем: 
 (10) пересекаются (имеют одну общую точку), т.е. существуют такие значения t и u, когда
(10) пересекаются (имеют одну общую точку), т.е. существуют такие значения t и u, когда  . Т.е.
. Т.е.  линейно независимы. Если две прямые, заданные уравнения (10) параллельны и их направляющие векторы а, b коллинеарны, т.е.
линейно независимы. Если две прямые, заданные уравнения (10) параллельны и их направляющие векторы а, b коллинеарны, т.е.  . Т.о.
. Т.о. 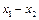 может быть представлен в виде линейной комбинации векторов а и b, т.е. в виде:
может быть представлен в виде линейной комбинации векторов а и b, т.е. в виде:  . Поэтому точка, радиус-вектором которой является этот вектор, есть точка пересечения данных прямых. Т.о. необходимым и достаточным условием того, что две прямые, заданные выражением (10), пересекаются или параллельны, является линейная зависимость тройки векторов
. Поэтому точка, радиус-вектором которой является этот вектор, есть точка пересечения данных прямых. Т.о. необходимым и достаточным условием того, что две прямые, заданные выражением (10), пересекаются или параллельны, является линейная зависимость тройки векторов  (13)
(13)


 :
: 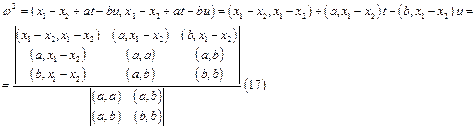 Общий перпендикуляр двух прямых. Требуем, чтобы отрезок, соединяющий произвольные точки двух данных прямых (10), был перпендикулярен направляющим векторам а и b обеих прямых. Мы получили условие (14), отсюда находим, что значение t и u, удовлетворяющие этому условию, совпадают со значением (15). Это совпадение показывает, что основания общего перпендикуляра двух прямых совпадают с теми точками эти прямых, расстояние между которыми минимально.
Общий перпендикуляр двух прямых. Требуем, чтобы отрезок, соединяющий произвольные точки двух данных прямых (10), был перпендикулярен направляющим векторам а и b обеих прямых. Мы получили условие (14), отсюда находим, что значение t и u, удовлетворяющие этому условию, совпадают со значением (15). Это совпадение показывает, что основания общего перпендикуляра двух прямых совпадают с теми точками эти прямых, расстояние между которыми минимально.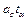 , где
, где 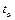 принимает все вещественные значения, то радиус-векторы точек m-плоскости имеют вид?
принимает все вещественные значения, то радиус-векторы точек m-плоскости имеют вид?  (1) – векторное уравнение m-плоскости. Векторы
(1) – векторное уравнение m-плоскости. Векторы 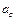 называются направляющими векторами m-плоскости.
называются направляющими векторами m-плоскости. ).
). (2) – параметрическое (координатное) уравнение m-плоскости в координатах.
(2) – параметрическое (координатное) уравнение m-плоскости в координатах. и векторы линейно независимы, то эти точки определяют единственную m-плоскость, проходящую через них. В этом случае за направляющие векторы этой плоскости можно принять векторы
и векторы линейно независимы, то эти точки определяют единственную m-плоскость, проходящую через них. В этом случае за направляющие векторы этой плоскости можно принять векторы  , и векторное уравнение m-плоскости может быть записано в виде:
, и векторное уравнение m-плоскости может быть записано в виде:  (3).
(3). - m-плоскостью
- m-плоскостью  .
. , мы получим уравнение (4):
, мы получим уравнение (4): 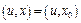 , или
, или 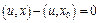 , или
, или  .
. - ортонормированный базис в n-мерном аффинном пространстве, тогда х можно разложить по этому базису:
- ортонормированный базис в n-мерном аффинном пространстве, тогда х можно разложить по этому базису:  . Тогда (4) можно записать, как
. Тогда (4) можно записать, как  (5).
(5). и вектор нормали u, то т.к.
и вектор нормали u, то т.к.  удовлетворяет уравнению (4), мы получаем, что
удовлетворяет уравнению (4), мы получаем, что  .
. (8).
(8). , при этом
, при этом  линейно независимы. Тогда уравнение плоскости будет иметь вид:
линейно независимы. Тогда уравнение плоскости будет иметь вид:  (9).
(9).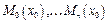 , то необходимым и достаточным условие того, что точки
, то необходимым и достаточным условие того, что точки  лежат на одной плоскости является линейная зависимость векторов
лежат на одной плоскости является линейная зависимость векторов  .
. , ортогональной вектору u. Формально принадлежность n+1 одной точки к плоскости записывают в виде равенства нулю определителя:
, ортогональной вектору u. Формально принадлежность n+1 одной точки к плоскости записывают в виде равенства нулю определителя:  (10) /
(10) / . Угол
. Угол  между плоскостями с векторами нормали u и v находится по формуле:
между плоскостями с векторами нормали u и v находится по формуле:  (11).
(11).