
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особливості методу вагових функційСодержание книги Поиск на нашем сайте
Синтез нерекурсивних цифрових фільтрів (НРЦФ або КІХ-фільтрів) може бути виконаний за заданою ідеалізованою частотною характеристикою фільтру Hd(jω) з нульовим запізнюванням і допустимими похибками її апроксимації. Враховуючи, що частотна характеристика і імпульсна характеристика пов'язані парою перетворень Фур'є, за допомогою зворотного перетворення Фур'є може бути знайдена імпульсна характеристика hd(n), яка відповідає заданій частотній характеристиці, що ідеалізується:
Проте імпульсна характеристика ідеального фільтру має нескінченну довжину і не відповідає умові фізичної реалізованості:
при n < 0 hd (n) ≠ 0 - відгук фільтру випереджає вхідну дію.
Тому вона не може бути безпосередньо використана в якості імпульсної характеристики НРЦФ. Наприклад, для цифрового ФНЧ (рис. 2) в основній смузі частот ± ωд/2
Аналітичні описи імпульсних характеристик інших типів ідеальних ЦФ приведені в п. 2.3.4. Рис. 2. Імпульсна характеристика ідеального ФНЧ
Отримати на основі імпульсної характеристики (3.4) КІХ-фільтр, що фізично реалізовується, з частотною характеристикою, близькою до заданої, можна шляхом зрушення hd (n) вправо на (N - 1) /2 відліків і усікання її за межами n < 0 і n ≥ N. При цьому частотна характеристика фільтру апроксимується усіченим рядом Фур'є з коефіцієнтами hd[n - (N - 1) /2]:
Відомо, що просте усікання ряду Фур'є супроводжується коливаннями Гіббса, що виникають при апроксимації розривних функцій. Для поліпшення якості апроксимації в методі вагових функцій імпульсну характеристику НРЦФ конструюють обмеженням довжини імпульсної характеристики hd[n - (N - 1) /2] за допомогою спеціальних вагових функцій або вікон w(n) кінцевої довжини N:
Наприклад, просте усікання еквівалентно множенню на прямокутну вагову функцію wR (n) =1, n=0,...N - 1. Отриманій таким чином імпульсній характеристиці відповідає частотна характеристика фільтру
що визначається згорткою в частотній області заданої частотної характеристики Hd (jω) з частотною характеристикою (Фур'є−образом) вагової функції W (jω):
де * - символ згортки, θ - змінна інтеграції, Ці перетворення в часовій і частотній області ілюструються графіками рис. 3, що досить наочно відбивають вплив вагового усікання на якість апроксимації заданої частотної характеристики усіченим рядом Фур'є. Частотна характеристика вагової функції на рис. 3 має головну пелюстку шириною ∆ωгл і бічні пелюстки, рівень яких характеризується максимальним по модулю значенням δбл.max і площею під бічними пелюстками. Згортка в частотній області здійснюється графічно шляхом зміщення по частоті в межах ± ωд/2 дзеркально відображеної частотної характеристики вагової функції і обчислення площі перекриття її із заданою частотною характеристикою Hd(jω).
Рис. 3. Графічна ілюстрація синтезу НРЦФ методом вагових функцій (ідеальний ФНЧ і прямокутна вагова функція)
З рисунка виходить, що перехідна смуга частотної характеристики фільтру H (jω) визначається шириною головної пелюстки частотної характеристики вагової функції: · мінімальну ширину головної пелюстки ∆ωгл; · мінімальний рівень бічних пелюсток δбл.max і мінімальну площу під бічними пелюстками; · мінімальну довжину N.
Вимоги ці досить суперечливі. Так, гладші вагові функції мають менший рівень бічних пелюсток, але велику ширину головної пелюстки, що зменшується зі збільшенням довжини вагової функції N. Цим пояснюється різноманіття використовуваних на практиці типів вагових функцій. Слід зазначити, що метод вагових функцій забезпечує строгу лінійність ФЧХ і постійність групового часу запізнювання фільтру зважаючи на парну або непарну симетрію отримуваною цим методом імпульсної характеристики: h (n) =h (N − 1 − n).
|
||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.244 (0.005 с.) |

 .
.


 .
.
 .
.
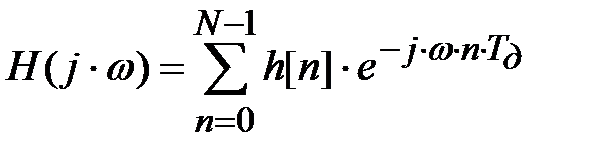 ,
,
 ,
, – частотна характеристика вагової функції.
– частотна характеристика вагової функції.
 , а похибки апроксимації (пульсації) в смузі пропускання і затримки δ1, δ2 пов'язані з рівнем її бічних пелюсток. Це визначає вимоги до вагової функції, яка повинна мати:
, а похибки апроксимації (пульсації) в смузі пропускання і затримки δ1, δ2 пов'язані з рівнем її бічних пелюсток. Це визначає вимоги до вагової функції, яка повинна мати:


