
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи розрахунку КІХ-фільтрівСодержание книги Поиск на нашем сайте Методи розрахунку КІХ-фільтрів Серед безлічі аналітичних/ітераційних методів розрахунку КІХ-фільтрів слід виділити два основні методи: · метод вагових функцій; · метод частотної вибірки. Крім того, можливе застосування числових методів розрахунку, серед яких виділяються наступні критерії розрахунку: · критерій мінімального середнього квадрата помилки (мінімального СКП); · критерій рівнохвилевого наближення. Більшість методів синтезу КІХ-фільтрів реалізована в пакеті програм MATLAB, і проектування не вимагає знання математичних виразів. Проте є випадки, коли можна швидко виконати синтез простих фільтрів в пакеті програм Mathcad.
Розрахунок усереднюючого фільтру Найбільш простим КІХ-фільтром можна вважати усереднюючий фільтр, який обчислює середньоарифметичне значення N відліків:
Коефіцієнти фільтру є відліками імпульсної характеристики h (k). Передатна функція фільтру дорівнює
Частотна характеристика обчислюється шляхом підстановки
Цей фільтр є цифровим ФНЧ, параметри якого залежать тільки від частоти дискретизації Змінюючи вказані параметри, можна підібрати частоту зрізу ФНЧ. Інші параметри фільтру при цьому забезпечити на заданому рівні складніше. Як приклад далі показаний розрахунок цифрового фільтру низьких частот (ФНЧ) усереднюючого типу з частотою зрізу Fзр=100 Гц.
Введення початкових даних
Розрахунок коефіцієнтів ЦФ
Розрахунок АЧХ ЦФ
Рис. 1. Результат розрахунку АЧХ цифрового фільтру
Перевірка значення АЧХ ЦФ на необхідній частоті зрізу
Видно, що значення АЧХ на необхідній частоті зрізу відрізняється від необхідного значення на рівні 0.7071. Отже, необхідно змінити порядок фільтру N, який спочатку дорівнював 20.
Підбір порядку фільтру N для забезпечення необхідної частоти зрізу
Можна переконатися, що при значенні N=35 забезпечується найменше відхилення коефіцієнта передачі на частоті зрізу від необхідного значення 0.7071.
Значення коефіцієнтів цифрового фільтру при цьому рівні
Розрахунок КІХ-фільтрів методом вагових функцій Види вагових функцій Проста вагова функція - прямокутна − має мінімальну ширину головної пелюстки і максимальний рівень бічних пелюсток.
Трикутна вагова функція є згорткой двох прямокутних вагових функцій завдовжки N/2:
У неї удвічі більша ширина головної пелюстки при досить великому рівні бічних пелюсток. Бічні пелюстки її мають ширину ∆ωбл=2 (ωд/N або ∆λбл=4 (π/N. Узагальнена вагова функція Хемінга описується вираженням
При α=0.5 вона відповідає ваговій функції Ханна, при α=0.54 - ваговій функції Хемінга. Рівень бічних пелюсток вагової функції Хемінга виявляється прийнятним для багатьох застосувань НРЦФ. Бічні пелюстки частотної характеристики мають ширину ∆ωбл=ωд/N або ∆λбл=2 (π/N. Площа під бічними пелюстками складає 0.04 % від площі квадрата частотної характеристики вагової функції.
Вагова функція Блекмана має вигляд
В порівнянні з ваговою функцією Хемінга у неї ширша головна пелюстка (у 1.5 рази) при дуже малому рівні бічних пелюсток. Ширина бічних пелюсток цієї вагової функції ∆ωбл = ωд/N або ∆λбл=2 (π/N. При синтезі НРЦФ використовуються також ефективні вагові функції Ланцоша, Дольфа-Чебишева, Каппелині, та ін. [7, 8], серед яких особливе значення має клас вагових функцій або вікон Кайзера.
Вагові функції Кайзера. На відміну від інших вагових функцій, що характеризуються постійними значеннями рівня бічних пелюсток δбл.max і відношення
де I0(x) − функція Бесселя нульового порядку.
Завдяки цьому забезпечується найкраща для цього методу синтезу якість апроксимації заданої частотної характеристики або найменший порядок фільтру при заданій якості апроксимації. Кайзером шляхом чисельної інтеграції згортки складена таблиця (таблиця. 2) і отримані емпіричні формули, які дозволяють безпосередньо по заданому згасанню Аз=|δ2max| (дБ) частотної характеристики H (jω), що апроксимує ідеальний ФНЧ, вибрати або розрахувати значення D- фактора і коефіцієнти β[5]:
По обчисленому або взятому з таблиці значенню D визначається необхідний порядок фільтру N≈D (fд/∆fпер, який округляється потім до найближчого більшого непарного числа. Як і для інших вагових функцій, у разі апроксимації ідеальних фільтрів типу СПФ, ПЗФ, БСФ згасання частотної характеристики в смузі затримання може бути менше його табличного значення, але не більше ніж на 6 дБ.
Таблиця 3.2
У таблиці 3.3 приведені також розрахункові значення рівня пульсацій частотної характеристики в смузі пропускання, згасання, що відповідають різним значенням, в смузі затримання [5]. Таблиця 3.3
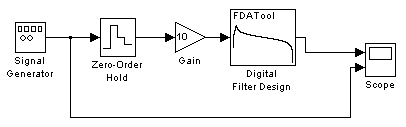
Створення моделі фільтру Для моделювання роботи цифрового фільтру (ЦФ) складемо наступну структурну схему (модель), рис. 3.6.
Рис. 3.6. Структурна схема для моделювання роботи цифрового фільтру
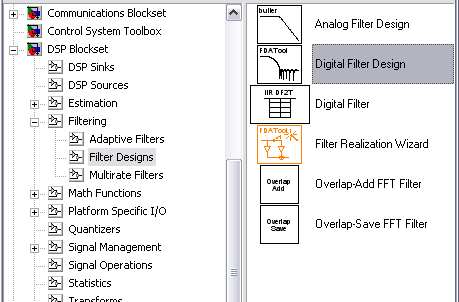
Модель цифрового фільтру створюється за допомогою блоку Digital Filter Design, рис. 3.7 (DSP Blockset/Filtering/Filter Design/ Digital Filter Design).
Рис. 3.7. Розташування блоку Digital Filter Design
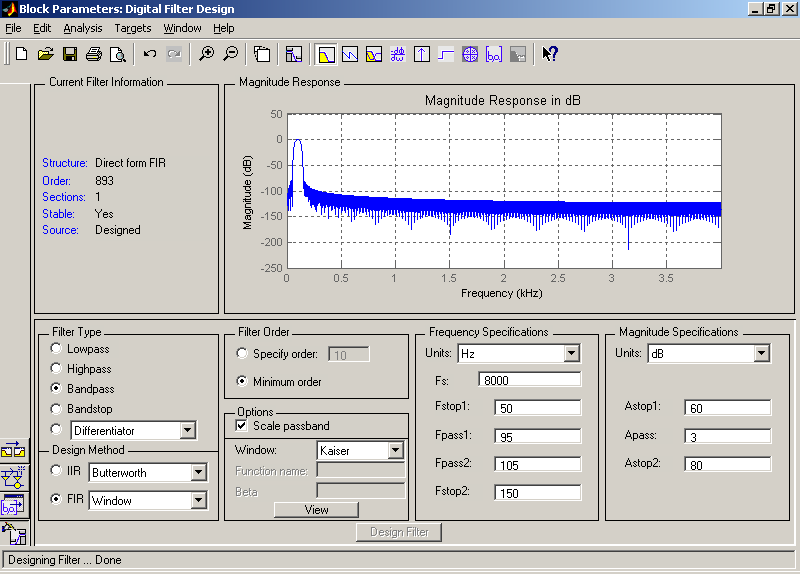
Початкові дані ЦФ задаються у блоці параметрів фільтру Block Parameteters: Digital Filter Design ( рис. 3.8).
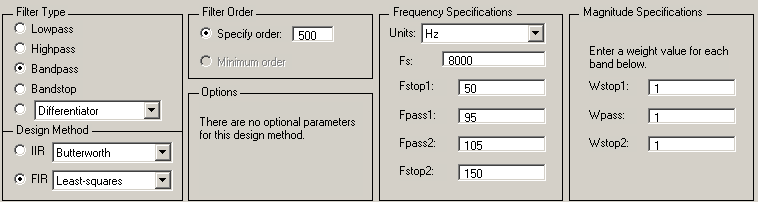
Рис. 3.8. Блок параметрів Digital Filter Design У блоці параметрів цифрового фільтру елементи налаштування зібрані в 6 груп: · Current Filter Information - відображається коротка інформація про цифровий фільтр (порядок - Order, стійкість - Stable/Unstable, кількість блоків - Sections, тип структури фільтру - Filter structure), що синтезується; · Filter Type - задається тип фільтру: · Lowpass - ФНЧ; · Highpass - ФВЧ; · Bandpass - смуговий фільтр СФ; · Bandstop - режекторний фільтр РФ; · Differentiator - диференціатори; · а також інші типи фільтрів; · Design Method - задається вид апроксимації: · IIR - БІХ-фільтри: · Butterworth - фільтр Баттерворта; · Chebyshev Type I - фільтр Чебишева 1 роду; · Chebyshev Type II - фільтр Чебишева 2 роди; · Elliptic - фільтр еліптичний (Золотарева-Кауера); · FIR - КІХ-фільтри, див. п. 2.3-2.5: · Equiripple - рівнохвилевий критерій розрахунку (мінімаксний), п. 2.5; · Least - squares - критерій мінімального СКП, п. 2.5; · Window - метод вагових (віконних) функцій, п. 2.3; · Filter Order - задається порядок фільтру-прототипу (Specify order) або виставляється прапорець розрахунку мінімального порядку фільтру-прототипу (Minimum order); · Frequency Specifications - задаються частотні параметри фільтру (кількість параметрів може змінюватися залежно від вибраного типу фільтру): · Units - одиниці виміру частоти (Hz - Гц, Normalized (0 to 1) - нормалізований фільтр (у відносних одиницях); · Fs - частота дискретизації; · Fstop1 - нижня частота смуги загородження (на якій забезпечується згасання Astop1, дБ); · Fpass1 - нижня частота смуги пропускання (на якій забезпечується згасання Apass, дБ); · Fpass2 - верхня частота смуги пропускання (на якій забезпечується згасання Apass, дБ); · Fstop2 - верхня частота смуги загородження (на якій забезпечується згасання Astop2, дБ); · Magnitude Specifications - задаються коефіцієнти згасання фільтру: · Units - одиниці виміру коефіцієнта згасання (dB - дБ, Squared - відносні одиниці); · Apass, Epass - коефіцієнти згасання в смузі пропускання; · Astop, Estop - коефіцієнти згасання в смузі загородження.
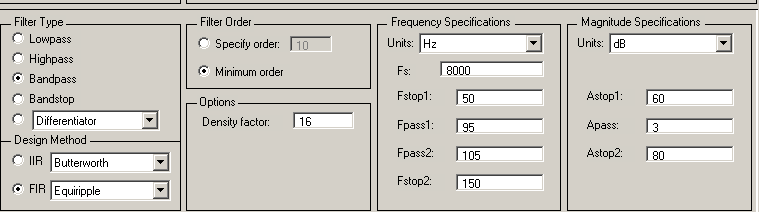
При виборі Equiripple равнохвилевогу методу розрахунку (мінімаксний критерій) необхідно додатково задати в групі Options (рис. 3.9) параметр Density factor, за замовчуванням рівний 16.
Рис. 3.9. Завдання параметра Options
При виборі Least - Squares критерію мінімального СКП необхідно додатково задати в групі Magnitude Specifications ( рис. 3.10) вагові коефіцієнти в смугах пропускання і затримання Wstop1, Wstop2, Wpass, за замовчуванням рівні 1.
Рис. 3.10. Завдання вагових коефіцієнтів в групі Magnitude Specifications
При виборі Window методу вагових функцій необхідно задати в групі Options (рис. 3.11) тип вагової функції Window, а також для деяких функцій додаткові параметри, наприклад параметр Beta для вагової функції Кайзера Kaiser.
Рис. 3.11. Вибір типу вагової функції Window
Основні вагові функції: · Bartlett - функція Бартлетта; · Blackman - функція Блекмана; · Hamming - функція Хемінга; · Hann - функція Ханна; · Kaiser - функція Кайзера; · Rectangular - прямокутна функція; · Triangular - трикутна функція;
Для управління параметрами відображення результатів розрахунку, графіків і виконання над ними різних дій блок параметрів Digital Filter Design має панель інструментів, що містить піктограми з наступними призначеннями:
Вікно Filter Visualization Tool дозволяє візуально проглянути такі параметри фільтру, як:
Блок Gain (підсилювач) Оскільки блок Digital Filter Design дозволяє розраховувати тільки нормовані фільтри, тобто з одиничним підсиленням в смузі пропускання, то для отримання коефіцієнтів передачі, що відрізняються від одиниці, необхідно використати додатковий блок підсилювача Gain (Simulink/ Math/ Gain), рис. 3.12.
Рис. 3.12. Розташування блоку Gain
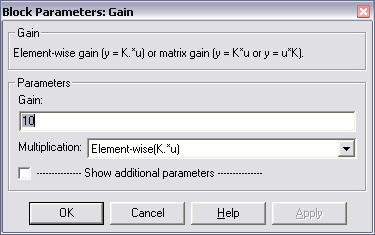
Коефіцієнт підсилення задається у вікні налаштування параметрів Block Parameters: Gain ( рис. 3.13).
Рис. 3.13. Вікно налаштування параметрів блоку Gain
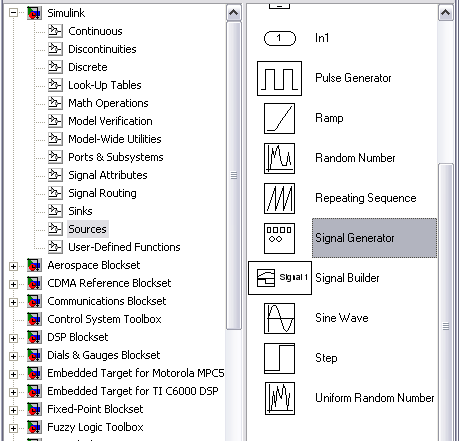
6.3 Блок Signal Generator (універсальний генератор сигналів) Для того, щоб подати на вхід фільтру сигнал, використовуються універсальний генератор сигналів Signal Generator (Simulink/ Sources/Signal Generator), рис. 3.14.
Рис. 3.14. Розташування блоку Signal Generator
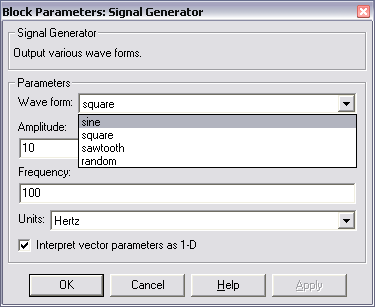
У вікні налаштування (рис. 3.15) блоку Signal Generator задаються наступні параметри: · Wave form - форма сигналу: · sine - синусоїдальний сигнал; · square - прямокутний сигнал; · saw tooth - пилкоподібний сигнал; · random - випадковий сигнал (шум); · Amplitude і Frequency - амплітуда і частота сигналу; · Units - одиниця виміру частоти (Hertz - Герци або rad/sec - рад/сік).
Рис. 3.15. Вікно налаштування параметрів блоку Signal Generator
Блок Step Блок Step (Simulink/ Sources/ Step), рис. 3.18.а, використовується для відтворення ступінчастої дії.
а)
б) Рис. 3.18. Розташування блоку Step (а) і вікно налаштування його параметрів (б) При відкритті вікна налаштування параметрів сигналу, рис 3.18.б, в графі Step time задається час початку ступінчастої дії, в графах Initial value і Final value - початкове і кінцеве значення амплітуди ступінчастої дії, в графі Sample time - період дискретизації вихідного сигналу (якщо період дорівнює нулю, то сигнал вважається безперервним). Щоб знайти відгук фільтру на одиничну ступінчасту дію (перехідну характеристику), треба скласти наступну структурну схему (рис. 3.19).
Рис. 3.19. Структурна схема для визначення перехідної характеристики фільтру
Блок Scope (осцилограф) Для візуального перегляду сигналів використовують блоки, які при моделюванні грають роль оглядових вікон; до них також відноситься блок Scope (осцилограф) (Simulink /Sinks/ Scope), рис. 3.20.
Рис. 3.20. Розташування блоку Scope Блок Scope має один вхід і дозволяє в процесі моделювання спостерігати процеси, що цікавлять користувача. Основним параметром осцилографа є кількість входів (тобто кількість сигналів, що відображаються, одночасно у вікні може відображатися до 30 сигналів). Залежно від кількості сигналів осцилограф може мати декілька екранів. Екран осцилографа з двома входами виглядає так, як показано на рис. 3.21 (піктограма виглядає так
Рис. 3.21. Екран осцилографа Scope з двома входами
Натиснення піктограми У графі Number of axes задається кількість входів осцилографа, Time range - верхня межа часу, що відображається на вісі абсцис, Tick labels - відображення вісей координат (all - усі осі, none - немає осей, bottom axis only - тільки горизонтальна вісь). Рекомендується використати налаштування, виставлені за замовчуванням.
Рис. 3.22. Вікно налаштування параметрів блоку Scope
КОНТРОЛЬНІ ПИТАННЯ
1. Що таке імпульсна характеристика і передатна функція ЦФ? 2. Що таке порядок ЦФ і як позначається його значення при реалізації фільтру? 3. Від яких параметрів залежить частотна характеристика ЦФ по алгоритму усереднювання? Який запис алгоритму роботи такого фільтру? 4. Який порядок розрахунку КІХ-фільтру методом вагових функцій? 5. Які вирази описують імпульсні характеристики ідеальних ЦФ: ФНЧ, СФ? 6. Яким чином записується критерій мінімуму середнього квадрата помилки (СКП) при розрахунку ЦФ чисельними методами? 7. Які основні методи і різновиди методів використовуються в пакеті програм MATLAB для розрахунку КІХ-фільтрів? 8. Які параметри фільтру дозволяє візуально проглянути вікно Filter Visualization Tool блоку параметрів Digital Filter Design? 9. Для чого використовується блок Gain при моделюванні роботи ЦФ? 10. Яке призначення блоку Zero - Order Hold при моделюванні роботи ЦФ? 11. Яким чином задається період дискретизації блоку Zero - Order Hold і чому він має бути рівний? 12. Які параметри необхідно встановити, щоб на виході блоку Step отримати безперервну/дискретну ступінчасту дію?
Синтез і реалізація НЦФ (до завдання 1) 13. Що є метою синтезу НЦФ? Чим відрізняються імпульсні характеристики (ІХ) РЦФ і НЦФ? 14. У чому полягає синтез НЦФ методом вагових функцій? 15. Які основні етапи синтезу НЦФ методом вагових функцій? 16. Як знаходиться ІХ НЦФ при синтезі методом вагових функцій? 17. Від чого залежить порядок(довжина ІХ) НЦФ, що синтезується методом вагових функцій? 18. Приведіть вирази для ІХ hd(n), відповідною заданою частотної характеристиці(ЧХ) Hd (jω). Чому коефіцієнти hd(n) розкладання заданої ЧХ Hd(jω) в ряд Фур'є не можуть бути використані в якості коефіцієнтів НЦФ, що синтезується? 19. Як виконується усікання ІХ, що відповідає заданою ЧХ Hd(jω)? 20. Як проявляється усікання на якості апроксимації заданої ЧХ Hd(jω)? 21. До чого призводить усікання ряду Фур'є (ІХ hd(n)) за допомогою вагових функцій кінцевої довжини? 22. Як виражається ЧХ фільтру, що синтезується, через ЧХ вагової функції і задану ЧХ? 23. Як пов'язані параметри ЧХ фільтру з параметрами вагової функції? 24. Який математичний алгоритм обробки реалізують НЦФ? 25. Як обчислюються відліки вихідного сигналу НЦФ відповідно до алгоритму ДВС? 26. Який об'єм пам'яті і обчислень потрібний для реалізації НЦФ на основі ДВС? 27. Чому дорівнює тривалість перехідного процесу в НЦФ? 28. Покажіть, як виконується дискретна часова згортка на прикладі прямокутного сигналу завдовжки N1 = 8відліків і прямокутною ІХ довжиною N2 =4. 29. Чому дорівнює тривалість вихідного сигналу НЦФ при вхідній дії кінцевої довжини N1? 30. Як впливає обмеження розрядності коефіцієнтів НЦФ? 31. За якої умови можуть бути відсутніми шуми квантування добутків в НЦФ? 32. Які початкові дані на синтез НЦФ і як вони використовуються в процесі синтезу? 33. Як залежить складність реалізації НЦФ від вимог, що пред'являються до його АЧХ?
Вагові функції, зв'язок параметрів ЧХ фільтру з параметрами вагової функції (до завдання 1) 34. Які типовий вид і параметри ЧХ вагової функції? 35. Які вимоги пред'являються до вагової функції? 36. До чого призводить зменшення довжини вагової функції? 37. Від чого залежить ширина головної пелюстки вагової функції? 38. Від чого залежить рівень бічних пелюсток вагової функції? 39. Як можна зменшити перехідну смугу НЦФ, що синтезується? 40. Як можна зменшити згасання в смузі затримання синтезованого НЦФ? 41. З яких умов вибирається тип вагової функції? 42. Чим відрізняються один від одного різні вагові функції? 43. Як забезпечується необхідне згасання АЧХ фільтру в смузі затримання? 44. Як здійснюється синтез НЦФ за допомогою вагових функцій Кайзера? 45. Як розраховується довжина вагової функції Кайзера? 46. У чому особливість і перевага вагових функцій Кайзера в порівнянні з іншими ваговими функціями? 47. Який типовий вид АЧХ НЦФ, синтезованого методом вагових функцій і чим він обумовлений? 48. Як досягається задане послаблення АЧХ ап на частотах зрізу НЦФ? 49. Яке послаблення АЧХ має місце на заданих частотах зрізу НЦФ при синтезі методом вагових функцій? 50. Чому метод вагових функцій відносять до ітераційних методів синтезу ЦФ? 51. Який вид має ФЧХ НЦФ і як вона описується математично? 52. Як визначається ГВЗ НЦФ, синтезованого методом вагових функцій? 53. Які вимоги пред'являються до ФЧХ НЦФ і як вони забезпечуються?
Синтез НЦФ методом частотної вибірки (до завдання 2) 54. Що є метою синтезу НЦФ на основі частотної вибірки (ЧВ)? Чим відрізняються імпульсні характеристики (ІХ) РЦФ і НЦФ? 55. У чому полягає синтез НЦФ методом ЧВ? 56. Які основні етапи синтезу НЦФ методом ЧВ? 57. Які початкові дані на синтез НЦФ і як вони використовуються в процесі синтезу? 58. Що таке ДПФ і ОДПФ і як вони використовуються при синтезі НЦФ на основі ЧВ? 59. Як здійснюється дискретизація заданої ЧХ? 60. Що таке дискретизована частотна характеристика (ДЧХ) ЦФ і яким чином її отримують? 61. Що таке перехідна смуга ЧХ фільтру, як вибирається число варійованих відліків в цій смузі при дискретизації ЧХ і їх значення? 62. Що є ОДПФ дискретизованої частотної характеристики ЦФ? 63. Що є ДПФ імпульсної характеристики (ІХ) НЦФ? 64. Як пов'язані між собою ІХ НЦФ з його, що дискретизованою частотною характеристикою? 65. Як виражається передатна функція НЦФ через ДЧХ? 66. Як здійснюється оптимізація (найкраще наближення до заданої АЧХ) в методі ЧВ? 67. Від чого залежить порядок (довжина ІХ) НЦФ, що синтезується методом ЧВ? 68. Як можна зменшити згасання в смузі затримання синтезованого НЦФ? 69. Як розраховується довжина ІХ НЦФ, що синтезується методом ЧВ? 70. Який типовий вид АЧХ НЦФ, синтезованого методом вагових функцій, і чим він обумовлений? 71. Який вид має ФЧХ НЦФ, синтезованого методом ЧВ, і як вона описується математично? 72. Як розміщуються нулі і полюси НЦФ на основі ЧВ, для чого необхідна компенсація полюсів нулями? 73. Чим визначається число точок і крок дискретизації ЧХ при синтезі НЦФ методом ЧВ? 74. Як забезпечується необхідна якість апроксимації заданої ЧХ в методі ЧВ? 75. Чому метод ЧВ відносять до ітераційних методів синтезу ЦФ, тобто до методів з варійованими параметрами? 76. Як знаходиться ІХ НЦФ, синтезованого методом ЧВ?
Реалізація НЦФ на основі частотної вибірки (до завдання 2) 77. Як виходить структурна схема НЦФ на основі ЧВ? 78. Від чого залежить складність реалізації НЦФ на основі ЧВ? 79. Як знаходиться відгук на одиничний імпульс НЦФ на основі ЧВ? 80. Як здійснюється обробка сигналу в НЦФ на основі ЧВ? 81. Який математичний опис алгоритму обробки сигналу в НЦФ на основі ЧВ? 82. Як визначається тривалість перехідного процесу в НЦФ на основі ЧВ? 83. Як залежить складність реалізації НЦФ на основі ЧВ від вимог, що пред'являються до його АЧХ? 84. Чим визначається кількість рекурсивних ланок в структурі НЦФ на основі ЧВ? 85. Як в структурі НЦФ на основі ЧВ перейти від ланок з комплексними коефіцієнтами до ланок з речовими коефіцієнтами? 86. Як знаходиться вихідний сигнал НЦФ на основі ЧВ і чому дорівнює його тривалість при вхідній дії кінцевої довжини N1? 87. Чому НЦФ на основі ЧВ ефективний при реалізації вузькосмугових фільтрів? 88. Для чого потрібне зміщення нулів і полюсів НЦФ на основі ЧВ всередину круга одиничного радіусу і як це відбивається на його реалізації? 89. Які причини можливої нестійкості НЦФ на основі ЧВ? 90. Як забезпечується стійкість НЦФ на основі ЧВ? 91. Як впливає на характеристики НЦФ на основі ЧВ зміщення полюсів-нулів всередину круга одиничного радіусу? 92. У чому відмінність структури і алгоритму обробки НЦФ ЧВ із зміщеними нулями-полюсами? 93. Які можливі варіанти реалізації НЦФ, синтезованого методом ЧВ? 94. Які переваги і недоліки реалізації НЦФ на основі ЧВ в порівнянні з іншими способами? 95. У яких випадках доцільне застосування НЦФ на основі ЧВ і чому? 96. Як знаходиться число обчислювальних операцій на один відлік сигналу при реалізації НЦФ на основі частотної вибірки? 97. Як визначається необхідний об'єм пам'яті при реалізації НЦФ на основі частотної вибірки? 98. Як відрізняються об'єми обчислень при реалізації синтезованого НЦФ на основі частотної вибірки і дискретної тимчасової згортки? 99. Як відрізняються об'єми обчислень при реалізації синтезованого НЦФ на основі частотної вибірки і дискретного(швидкого) перетворення Фур'є? Методи розрахунку КІХ-фільтрів Серед безлічі аналітичних/ітераційних методів розрахунку КІХ-фільтрів слід виділити два основні методи: · метод вагових функцій; · метод частотної вибірки. Крім того, можливе застосування числових методів розрахунку, серед яких виділяються наступні критерії розрахунку: · критерій мінімального середнього квадрата помилки (мінімального СКП); · критерій рівнохвилевого наближення. Більшість методів синтезу КІХ-фільтрів реалізована в пакеті програм MATLAB, і проектування не вимагає знання математичних виразів. Проте є випадки, коли можна швидко виконати синтез простих фільтрів в пакеті програм Mathcad.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 .
.
 .
.

 .
.
 і порядку фільтру N.
і порядку фільтру N.






 .
.
 .
.
 .
.
 (D- фактор) у вагових функцій Кайзера ці параметри можуть широко варіюватися за допомогою коефіцієнта β, того, що входить в математичний вираз цієї функції:
(D- фактор) у вагових функцій Кайзера ці параметри можуть широко варіюватися за допомогою коефіцієнта β, того, що входить в математичний вираз цієї функції: ,
,




 створити новий блок налаштування параметрів ЦФ;
створити новий блок налаштування параметрів ЦФ; відкрити блок налаштування параметрів ЦФ;
відкрити блок налаштування параметрів ЦФ; зберегти налаштування блоку параметрів ЦФ;
зберегти налаштування блоку параметрів ЦФ; друк вмісту вікна;
друк вмісту вікна; вікно для попереднього перегляду перед друком вмісту вікна;
вікно для попереднього перегляду перед друком вмісту вікна; відмінити останню дію;
відмінити останню дію; повернутися на крок назад;
повернутися на крок назад; збільшення вмісту вікна;
збільшення вмісту вікна; зменшення вмісту вікна;
зменшення вмісту вікна; висновок в окремому вікні Filter Visualization Tool параметрів синтезованого фільтру.
висновок в окремому вікні Filter Visualization Tool параметрів синтезованого фільтру. АЧХ фільтру;
АЧХ фільтру; ФЧХ фільтру;
ФЧХ фільтру; одночасно в одному вікні і АЧХ і ФЧХ фільтру;
одночасно в одному вікні і АЧХ і ФЧХ фільтру; імпульсна характеристика;
імпульсна характеристика; реакція фільтру на ступінчасту дію (перехідна характеристика);
реакція фільтру на ступінчасту дію (перехідна характеристика); картина нулів і полюсів фільтру на комплексній Z- площині;
картина нулів і полюсів фільтру на комплексній Z- площині; значення коефіцієнтів передатної функції фільтру (Numerator - коефіцієнти чисельника, Denominator - коефіцієнти знаменника).
значення коефіцієнтів передатної функції фільтру (Numerator - коефіцієнти чисельника, Denominator - коефіцієнти знаменника).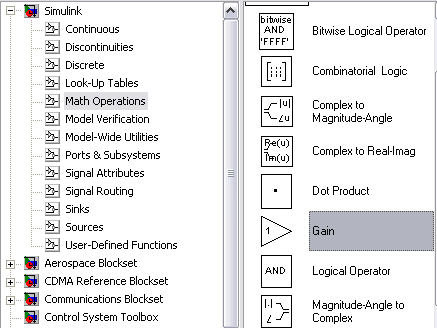




 ).
).
 призводить до появи вікна налаштування параметрів Scope (Scope parameters), рис. 3.22.
призводить до появи вікна налаштування параметрів Scope (Scope parameters), рис. 3.22.



