
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибір вагової функції і порядок розрахункуСодержание книги Поиск на нашем сайте
У таблиці. 1 приведені використовувані при синтезі ЦФ параметри вагових функцій: прямокутною, трикутною, Ханна, Хемінга і Блекмана. Окрім значень ширини головної пелюстки ∆ωгл = D (ωд/N, де D − так званий D-фактор, і максимального рівня бічних пелюсток δбл.max вони включають також оціночні значення похибки апроксимації частотної характеристики в смузі затримання (максимальні пульсації частотної характеристики) |δ2max|, дБ, розраховані для цифрового ФНЧ з частотою зрізу Для ЦФ з двома і більше частотами зрізу (СПФ, ПЗФ, БСФ) залежно від конкретних даних погрішність апроксимації може бути більше її оцінного значення, але не більше ніж 6 дБ. Таблиця 3.1
Крок 1. Керуючись цими таблиці 3.1, по необхідному згасанню частотної характеристики в смузі затримання Аз можна зробити вибір типу вагової функції.
Крок 2. Для вибраної вагової функції і заданої перехідної смуги частотної характеристики фільтру
де D - коефіцієнт, залежний від типу вагової функції (D- фактор). Значення N прирівнюється найближчому цілому числу, зазвичай непарному.
Крок 3. В якості частот зрізу заданої частотної характеристики використовують їх розрахункові значенняFзр2р, зміщені в смугу затримання приблизно на половину перехідної смуги фільтру ∆fпер. Це пов'язано з властивим цьому методу розмиванням меж переходу від смуги пропускання фільтру до смуги затримання (рис. 3.3). Наприклад, для СФ:
Крок 4. Знаходиться імпульсна характеристика фільтру шляхом вагового усікання зміщеної управо на (N − 1) /2 відліків імпульсної характеристики hd (m):
Крок 5. Розраховується АЧХ фільтру.
і перевіряється її відповідність початковим даним по нерівномірності частотної характеристики в смузі пропускання Aп і згасанню в смузі затримання Aз.
Крок 6. Оскільки цей метод не забезпечує точної відповідності початкових і розрахункових даних (є ітераційним), при необхідності коригуються значення розрахункових частот зрізу Fзр1р, Fзр2р і довжини фільтру N і розрахунки повторюються.
Види вагових функцій Проста вагова функція - прямокутна − має мінімальну ширину головної пелюстки і максимальний рівень бічних пелюсток.
Трикутна вагова функція є згорткой двох прямокутних вагових функцій завдовжки N/2:
У неї удвічі більша ширина головної пелюстки при досить великому рівні бічних пелюсток. Бічні пелюстки її мають ширину ∆ωбл=2 (ωд/N або ∆λбл=4 (π/N. Узагальнена вагова функція Хемінга описується вираженням
При α=0.5 вона відповідає ваговій функції Ханна, при α=0.54 - ваговій функції Хемінга. Рівень бічних пелюсток вагової функції Хемінга виявляється прийнятним для багатьох застосувань НРЦФ. Бічні пелюстки частотної характеристики мають ширину ∆ωбл=ωд/N або ∆λбл=2 (π/N. Площа під бічними пелюстками складає 0.04 % від площі квадрата частотної характеристики вагової функції.
Вагова функція Блекмана має вигляд
В порівнянні з ваговою функцією Хемінга у неї ширша головна пелюстка (у 1.5 рази) при дуже малому рівні бічних пелюсток. Ширина бічних пелюсток цієї вагової функції ∆ωбл = ωд/N або ∆λбл=2 (π/N. При синтезі НРЦФ використовуються також ефективні вагові функції Ланцоша, Дольфа-Чебишева, Каппелині, та ін. [7, 8], серед яких особливе значення має клас вагових функцій або вікон Кайзера.
Вагові функції Кайзера. На відміну від інших вагових функцій, що характеризуються постійними значеннями рівня бічних пелюсток δбл.max і відношення
де I0(x) − функція Бесселя нульового порядку.
Завдяки цьому забезпечується найкраща для цього методу синтезу якість апроксимації заданої частотної характеристики або найменший порядок фільтру при заданій якості апроксимації. Кайзером шляхом чисельної інтеграції згортки складена таблиця (таблиця. 2) і отримані емпіричні формули, які дозволяють безпосередньо по заданому згасанню Аз=|δ2max| (дБ) частотної характеристики H (jω), що апроксимує ідеальний ФНЧ, вибрати або розрахувати значення D- фактора і коефіцієнти β[5]:
По обчисленому або взятому з таблиці значенню D визначається необхідний порядок фільтру N≈D (fд/∆fпер, який округляється потім до найближчого більшого непарного числа. Як і для інших вагових функцій, у разі апроксимації ідеальних фільтрів типу СПФ, ПЗФ, БСФ згасання частотної характеристики в смузі затримання може бути менше його табличного значення, але не більше ніж на 6 дБ.
Таблиця 3.2
У таблиці 3.3 приведені також розрахункові значення рівня пульсацій частотної характеристики в смузі пропускання, згасання, що відповідають різним значенням, в смузі затримання [5]. Таблиця 3.3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.118.36 (0.01 с.) |

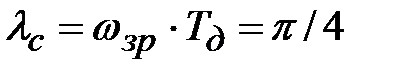 . Такі ж похибки мають місце і при синтезі ФВЧ.
. Такі ж похибки мають місце і при синтезі ФВЧ.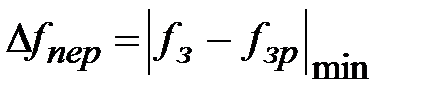 відповідно до наближеного співвідношення ∆fгл=∆fпер=D (fд/N знаходиться необхідна довжина вагової функції і визначувана нею довжина імпульсної характеристики фільтру:
відповідно до наближеного співвідношення ∆fгл=∆fпер=D (fд/N знаходиться необхідна довжина вагової функції і визначувана нею довжина імпульсної характеристики фільтру: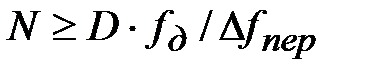 ,
,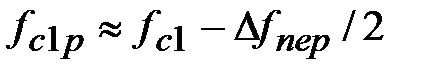 ;
; 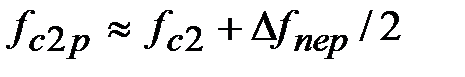 .
.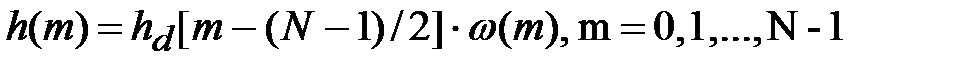 .
.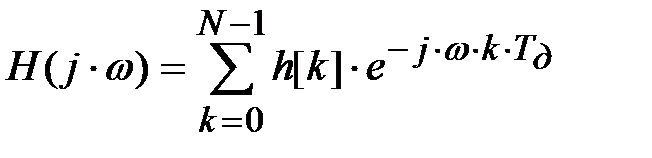

 .
.
 .
.
 (D- фактор) у вагових функцій Кайзера ці параметри можуть широко варіюватися за допомогою коефіцієнта β, того, що входить в математичний вираз цієї функції:
(D- фактор) у вагових функцій Кайзера ці параметри можуть широко варіюватися за допомогою коефіцієнта β, того, що входить в математичний вираз цієї функції: ,
,






