
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения энергии для механических процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одним из наиболее фундаментальных законов природы является закон сохранения энергии, согласно которому важнейшая физическая величина – энергия – сохраняется в изолированной системе. Закон сохранения энергии: в изолированной системе энергия может переходить из одной формы в другую, но ее количество остается постоянным. Если система не изолирована, то ее энергия может изменяться либо при одновременном изменении энергии окружающих тел на такую же величину, либо за счет изменения энергии взаимодействия тела с окружающими телами. При переходе системы из одного состояния в другое изменение энергии не зависит от того, каким способом (в результате каких взаимодействий) происходит переход, т.е. энергия – однозначная функция состояния системы. Закон сохранения энергии является строгим законом природы, справедливым для всех известных взаимодействий. Согласно известной теории Э. Нётер, он связан с однородностью времени, т.е. с тем фактом, что все моменты времени эквивалентны и физические законы не меняются со временем. Закон сохранения энергии для механических процессов был установлен Г. Лейбницем (1686) а для немеханических – в середине XIX в. Ю.Р. Майером (1845), Дж. Джоулем и Г. Гельмгольцем (1847). В термодинамике закон сохранения энергии называется первым началом термодинамики. Открытие закона сохранения и превращения энергии вначале было итогом развития механики. Но затем, благодаря дальнейшим экспериментальным исследованиям и теоретическому осмысливанию их результатов, становилось ясно, что содержание этого закона значительно глубже, что он – всеобщий закон природы. Это позволило быстрыми темпами развивать теорию тепловых процессов, что привело к появлению термодинамики. Особо важную роль закон сохранения и превращения энергии сыграл в изучении электрических и магнитных явлений, своеобразие и специфика которых не допускали применения других механических (по своему происхождению) понятий. Становление и утверждение закона сохранения энергии охватывает длительный период – более полутораста лет. Как уже указывалось, первым был установлен закон сохранения энергии для механического движения. Первый период был связан с длительной дискуссией о так называемых «мерах движения» и введением понятия «работа». В первой половине XVII в. Р. Декарт ввел понятие меры движения — количество движения, или импульс, которое в современных обозначениях выглядит следующим образом: Р = mv, где т – масса (во времена Декарта понятия массы т еще не было), v – скорость (Р и v – векторные величины). Понятием количества движения, равного mv, пользовались многие ученые того времени, в том числе и И. Ньютон. Однако в 1686 г. появилась статья Г. Лейбница «Краткое доказательство ошибки Декарта... о количестве движения...», в которой он в качестве меры движения предлагал считать величину mv2, названную им «живой силой». «Живая сила» при определенных условиях в механических движениях была величиной постоянной. По Лейбницу, основной закон природы состоит не в сохранении количества движения, но в том, что необходимо сохранить одно и то же количество двигательной деятельности, которое означает совсем не то, что понимают сторонники Декарта под количеством движения. При введении меры движения в виде величины mv2 Лейбниц рассуждал следующим образом. Известно, что для поднятия тела весом в 1 фунт на высоту в 4 локтя требуются такие же усилия, как и для поднятия веса тела в 4 фунта на 1 локоть. Если же предоставить этим телам возможность падать, то в момент касания земли скорость первого тела будет в два раза больше скорости второго ( Это произведение mv2 он и выбрал в качестве меры движения. «Живая сила» (mv2), по мнению Лейбница, выражает то «количество двигательной деятельности, которое сохраняется в природе». Теперь мы знаем, что mv2 есть удвоенная кинетическая энергия движущегося тела. Таким образом, Лейбниц, по сути, вначале сформулировал закон сохранения кинетической энергии. Кинетическая энергия, по современной терминологии, определяется как физическая величина, равная половине произведения массы частицы на квадрат ее скорости: Основанием послужила теорема, доказанная за несколько лет до этого французским математиком Л.Н. Карно. Согласно его теореме, если тело движется под действием постоянной силы, то удвоенное произведение силы (F) на перемещение (s) равно разности «живых сил» в конце и начале перемещения:
Тогда это было новым словом в практической механике. Произведение силы на перемещение в формуле (2.1) Г. Кориолис вслед за другим французским механиком, Ж.В. Понселе, назвал работой. Если работу обозначить через А и записать как A = Fs, то формулу следует переписать в виде:
Появившиеся в знаменателях этой формулы двойки дали основание Г. Кориолису принять за меру движения половину лейбницевой «живой силы». Теорему, выраженную формулой, принято называть теоремой о кинетической энергии. В соответствии с ней работа сил, действующих на тело, равна изменению кинетической энергии этого тела: А = EK2-EK1=ΔEK. Из теоремы следует, что кинетическая энергия равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему заданную скорость движения. Следующий важный шаг в развитии понятия механической энергии был сделан Г. Гельмгольцем, чей вклад в обоснование закона сохранения энергии будет более подробно рассмотрен ниже. Изучая движение тел под действием сил, которые постоянны или зависят от расстояния, но не от времени и скорости, он обратил внимание на то, что левую часть уравнения в таком случае всегда можно представить в виде разности значений некоторой величины, характеризующей взаимодействие рассматриваемых тел. Поскольку новая величина имела такую же размерность, что и «живая сила», Г. Гельмгольц предложил и ее назвать «силой», но не «живой», а «напряженной». Впоследствии «напряженная сила» Гельмгольца была переименована в потенциальную энергию. Потенциальная энергия – это энергия взаимодействия. Она определяется работой, которую должны совершить силы, чтобы переместить тело из данного положения в нулевое: ЕП=А1 – 0. Выбор нулевого положения произволен. Поэтому потенциальная энергия определена неоднозначно: по отношению к разным нулевым уровням потенциальная энергия одного и того же тела будет различной. Например, потенциальная энергия тела, взаимодействующего с Землей, может быть найдена по формуле ЕП = mgh, где h — высота центра тяжести тела, отсчитываемая от нулевого уровня. Принимая за нулевой уровень поверхность Земли, пола в комнате или, наконец, стола, над которым находится рассматриваемое тело, мы получим разные значения h и соответственно разные значения потенциальной энергии. Для потенциальной энергии справедлива теорема, аналогичная теореме о кинетической энергии. По теореме о потенциальной энергии, работа консервативных сил при любом движении тела равна разности потенциальных энергий в начальном и конечном состояниях: А = ЕП1 – ЕП2 = –ЕП. Рассматривая консервативные системы, т.е. системы, в которых действуют лишь консервативные силы, Гельмгольц пришел к выводу, что одна и та же величина может быть выражена и через приращение кинетической энергии системы, и через убыль ее потенциальной энергии. Это означает, что увеличение кинетической энергии рассматриваемой системы всегда сопровождается соответствующим уменьшением ее потенциальной энергии, и наоборот:
Если переписать равенство в виде
то станет ясно, что сумма кинетической и потенциальной энергий рассматриваемой системы в процессе ее движения не меняется. На основании этого можно объединить обе величины в одну — полную механическую энергию системы: Е = ЕК + ЕП. Из отношения следует, что Е = const. Итак, при любых процессах, происходящих в консервативной системе, ее полная механическая энергия остается неизменной. Это утверждение называется законом сохранения механической энергии. Поскольку кинетическую энергию Г. Гельмгольц называл «живой силой», а потенциальную энергию – «напряженной», то первая формулировка закона сохранения энергии, данная Гельмгольцем, такова: Когда тела природы действуют друг на друга с силами притяжения или отталкивания, не зависимыми от времени и скорости, то сумма живых сил и напряженных сил остается постоянной. Следующий этап установления закона сохранения и превращения энергии связан с изучением превращения различных форм энергии друг в друга. На начальном этапе изучения превращения различных форм движения друг в друга исключительную роль сыграл С. Карно, который впервые занялся изучением вопроса превращения теплоты в работу паровых машин. Поставив вначале достаточно скромную техническую задачу, как наиболее экономно использовать топливо в паровых машинах, он решил не только эту проблему, но и получил целый ряд принципиально новых результатов, имеющих важное значение для развития многих направлений естествознания. Во-первых, С. Карно нашел наиболее оптимальные условия работы тепловой машины (цикл Карно), при которых можно добиться максимального коэффициента ее полезного действия. Теорема Карно о максимальном коэффициенте полезного действия тепловых машин сыграла в дальнейшем важную роль в установлении одного из фундаментальных законов природы — второго начала термодинамики. Затем, продолжая свои исследования, он пришел к правильным взглядам на природу теплоты, как на совокупность механического движения атомов, из которых состоят физические тела. Он отмечал: Тепло – не что иное, как движущая сила или, вернее, как движение, изменившее свой вид, – это движение частиц тела,- повсюду, где происходит уничтожение движущей силы, возникает одновременно теплота в количестве, пропорциональном количеству исчезнувшей движущей силы. Обратно: всегда при исчезновении тепла возникает движущая сила. Таким образом, можно высказать общее положение: движущаяся сила существует в природе в неизменном количестве; она, собственно говоря, никогда не создается, никогда не уничтожается; в действительности она меняет форму, т.е. вызывает то один род движения, то другой, но никогда не исчезает. Как видно из приведенной цитаты, С. Карно сформулировал закон сохранения и превращения «сил» (по современной терминологии – энергии), закон сохранения и превращения тепловой и механической энергии. Он даже впервые приблизительно определил механический эквивалент теплоты. По некоторым представлениям, которые у меня сложились относительно теории теплоты, – писал Карно, – создание единицы движущей силы(по современной терминологии – единицы механической работы) требует затраты 2,7 единицы тепла. При переводе в современные единицы это значение механического эквивалента равно примерно 370 кГм/ккал. Противоположную С. Карно задачу, а именно: исследование обратного процесса превращения работы в тепло в результате трения, поставил себе Б. Томпсон. Работая на пушечных заводах, он заметил, что при сверлении пушечных стволов они очень сильно нагреваются. Он помещал пушечный металлический ствол в воду и в результате сверления доводил температуру воды до кипения и испарения. Подсчитав, сколько необходимо энергии для испарения воды, он установил равенство между этой энергией и механической работой при сверлении стволов пушек. Б. Томпсон также пришел к выводу, что теплота есть форма движения.
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.250 (0.014 с.) |

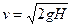 ). Значит, они будут обладать разным количеством движения (mv — по Декарту). Но если взять произведение массы т на v2, то mv2 будет величиной, одинаковой для обоих тел.
). Значит, они будут обладать разным количеством движения (mv — по Декарту). Но если взять произведение массы т на v2, то mv2 будет величиной, одинаковой для обоих тел. . Это уже знакомая «живая сила» Лейбница, только разделенная пополам. Разделить ее на два предложил французский механик Г. Кориолис.
. Это уже знакомая «живая сила» Лейбница, только разделенная пополам. Разделить ее на два предложил французский механик Г. Кориолис. .
. .
. .
. ,
,


