
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: статистичний розподіл.
ЯВИЩА ПЕРЕНОСУ ПЛАН 1. Розподіл Максвелла. 2. Розподіл Больцмана. 3. Середнє число зіткнень і середня довжина вільного пробігу молекул. 4. Явища переносу.
1. В ідеальному газові швидкості молекул мають різні напрямки, а величини цих швидкостей безперервно змінюються. Тому неможливо визначити кількість молекул, які мають конкретну швидкість, але можна підрахувати кількість молекул, які володіють швидкістю в інтервалі від v1 до v2. Це зробив англійський фізик Максвелл у 1859 році: він розглянув газ як сукупність великої кількості однакових молекул, котрі знаходяться у стані термодинамічної рівноваги за відсутності зовнішнього силового поля.
Застосувавши теорію ймовірності, він установив такий закон:
- розподіл молекул за швидкостями Максвелла.
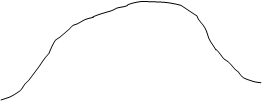
Із статистичного характеру розподілу молекул за швидкостями виходить: 1.Який би не був початковий розподіл молекул у термодинамічній рівноважній системі, завжди встановлюється розподіл Максвелла. 2. Якщо у системі вже встановився розподіл Максвелла, то він буде існувати нескінченно довго. Заштрихована площа вказує на кількість молекул dN, які знаходяться в інтервалі швидкостей від v до v + dv. Дослідивши на екстремум функцію (1), можна одержати ті значення швидкостей, при яких функція має максимум. Вони відповідають найбільш імовірній швидкості.
Крива розподілу дає можливість знайти також середнюарифметичну швидкість для кожної молекули.
- середня арифметична швидкість.
2. Розглянемо газ, який знаходиться у полі сили тяжіння. Для подальшого розгляду введемо такі припущення: розглянемо дуже тонкий шар газу (g=const), тоді
h
mg
- барометрична формула. Вона дає залежність атмосферного тиску від висоти h. Оскільки P = nkT, тоді (4) можна представити так:
- розподіл Больцмана. Цей вираз описує найзагальніший закон Больцмана і дає розподіл кількості частинок у будь-якому потенціальному полі.
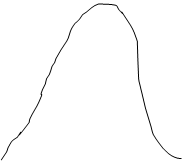
Ці теоретичні викладки були підтверджені в дослідах французького фізика Перрена (1908 рік), який вивчав розподіл по висоті посудини дуже маленьких частинок емульсії смоли гумігуту у воді і одержав такий закон:
3. Раніше ми розглядали властивості тіл та систем, які знаходились у стані рівнодинамічної рівноваги. Але в більшості випадків на практиці мають справу з неврівноваженими системами. Процес установлення стану термодинамічної рівноваги називається кінетичним процесом, або релаксаційним процесом, або просто релаксацією. Кількісною мірою встановлення стану термодинамічної рівноваги є величина, що називається час релаксації ( Молекули ідеального газу здійснюють хаотичний рух унаслідок зіткнення та внаслідок співударів змінюють величину і напрямок своїх швидкостей, тому виникає необхідність увести середнє число зіткнень за 1 секунду Відстань, яку проходять молекули між двома послідовними зіткненнями, називається середньою довжиною вільного пробігу молекул Ці величини пов`язані наступним співвідношенням:
Якщо вважати, що молекули газу можна уявити, як маленькі кульки, то нескладні розрахунки можуть привести до такого результату:
d - ефективний діаметр молекули.
Ефективний діаметр молекули - це відстань між центрами двох молекул при їх зіткненні.
Підстановка (7) в (6) дає:
- формула довжини середнього вільного пробігу молекул газу. Якщо врахувати, що
4. Розглянемо встановлення стану термодинамічної рівноваги у термодинамічно не врівноваженій системі. Молекули володіють масою, імпульсом та енергією. Тому в термодинамічно не врівноваженій системі при встановленні стану термодинамічної рівноваги буде відбуватися просторовий перенос маси, імпульсу та енергії, що зумовлює явища дифузії, внутрішнього тертя й теплопровідності відповідно. Ці явища зумовленi порушенням хаотичностi у русi молекул i описуються дослiдними законами. а) Дифузiя - це явище проникнення молекул однiєї речовини у мiжмолекулярний простiр другої.
Це явище описується дослiдним законом Фiка:
Закон Фiка:м аса речовини М, яка переноситься за час t через поверхню площею S перпендикулярно до напрямку змiнення густини
D - коефiцiєнт дифузiї. Фiзичний змiст D: вiн чисельно дорiвнює масі речовини, яка переноситься через одиничну поверхню за одиницю часу при одиничному градiєнті густини.
вiдстанi Х. б) Внутрiшнє тертя (в`язкiсть) - це явище, що виникає мiж шарами рiдини (газу), якi рухаються з рiзними швидкостями. Тертя зумовлене обмiном імпульсу молекул цих шарiв унаслiдок хаотичностi їх руху. Воно описується дослiдним законом Ньютона:
Сила тертя прямо пропорцiйна градiєнту швидкостi та площi шарiв, мiж якими виникає тертя.
Фiзичний змiст
в) Теплопровiднiсть - це явище переносу теплоти вiд бiльш "гарячого" шару з температурою Т1 до бiльш "холодного" з температурою Т2. (Т2 < Т1). Воно описується дослiдним законом Фур`є:
Теплота, що переноситься за час t через поверхню площею S прямо пропорцiйна градiєнту температури К - коефiцiєнт теплопровiдностi. Фiзичний змiст К: К чисельно дорiвнює кiлькостi теплоти Q, яка переноситься за одиницю часу через одиничну поверхню при одиничному градiєнтi температури Знак "- " указує на: 1). математично: перенос маси, iмпульсу та енергiї вiдбувається у напрямку зменшення градiєнтiв густини, швидкості та температури; 2). фiзично: термодинамічна система переходить iз неврiвноваженого стану в рiвноважний тiльки таким чином, а не iнакше.
Одна iз головних задач молекулярної теорiї - встановлення зв`язку мiж макропараметрами D,
У припущеннi, що молекули є кульки, можна показати:
CV - питома теплоємнiсть речовини при сталому об'ємі. Із (12) випливає:
Лекція IX ТЕМА: ОСНОВИ ТЕРМОДИНАМІКИ ПЛАН 1. Внутрiшня енергiя. 2. Теплота i робота. 3. Перший початок термодинамiки. 4. Теплоємнiсть багатоатомних газiв. 5. Адiабатичний процес. Рiвняння Пуассона. 6. Оборотнi та необоротнi процеси. Цикл. 7. Цикл Карно і його коефiцiєнт корисної дiї. 8. Другий початок термодинамiки. Ентропiя.
1. Кожна термодинамічна система характеризується повною енергiєю, в яку входять: 1) кінетична енергія механічного руху системи як цiлого у просторi або її макрочастинок; 2) потенціальна енергія, яка залежить вiд положення системи в зовнiшньому силовому полi; 3) внутрiшня енергiя U, яка залежить вiд внутрiшнього стану системи. Внутрішня енергія мiстить у собi: 1) кінетичну енергію поступального та обертального руху молекул; 2) потенціальну енергію їх взаємодiї; 3) енергiю коливального руху молекул, електронних оболонок і ядер. Слiд сказати, що внутрішня енергія є функцiєю параметрiвстану системи (перехiд системи з одного стану в iнший не залежить вiд способу переходу цiєї системи з одного стану в iнший).
В iдеальному газi потенціальна енергія взаємодiї молекул дорiвнює 0. У термодинаміцi не враховується внутрiшньомолекулярна та внутрiшньоядерна енергiя, тому внутрішня енергія iдеального газу однозначно повинна дорiвнювати кінетичній енергії молекул.
Нам відомо, що для однієї молекули а для одного моля
2. Змiна стану системи зумовлена передачею енергiї вiд одного тiла системи до iншого, а передача енергiї вiдбувається або у формi виконаної механічної роботи А, або у формi передачi теплоти Q.
Kiлькiсть теплоти Q - це фiзична величина, яка чисельно дорiвнює кiлькостi енергiї, що передається вiд одної системи до iншої внаслiдок теплообмiну.
Вiдомо, що теплота Q i робота А як двi форми передачi енергiї тiсно пов`язанi одна з одною. Одержимо вираз для роботи А при розширеннi газу:
dh
Якщо А>0, то газ звершує роботу при розширеннi. Якщо А<0, то робота звершується над газом, унаслiдок чого вiн стискується. Розглянемо вираз для роботи для рiзних iзопроцеciв: 1). i зохоричний: V = const; dV = 0;
2). iзобаричний:
3). iзотермiчний:
3. Перший початок термодинаміки зумовлює закон збереження та перетворення енергiї стосовно теплових процесiв i формулюється так:
Теплота Q, яка надається системi, при змiнi її стану витрачається на змiну її внутрішньої енергiї
- перший початок термодинамiки.
Iснує iнше формулювання:
Неможливий вiчний двигун першого роду
Вiчним двiгуном першого роду називають перiодично дiючий двигун, який звершує роботу в кiлькостях бiльших, нiж енергiя, яка пiдводиться зовнi. При розв’язанні багатьох практичних завдань є необхiднiсть запису (3) у диференцiальній формi:
де dU - повний диференцiал.
Фiзичний змiст: Для неповного диференцiала будь-якої функцiї спостерiгається залежнiсть вiд напрямку змiни, а для повного диференцiала цього не має. Для повного диференцiала змiна функцiї залежить тiлькi вiд початкового та кiнцевого станiв.
Застосуємо перший початок термодинаміки до iзопроцесiв:
1). iзохоричний: V = const; dV = 0;
2). iзотермiчний: T = const; dT = 0;
3). iзобаричний: P = const;
4. Для характеристики теплових властивостей тiл у термодинаміцi широко застосовують поняття теплоємностi:
Теплоємнiсть - це величина, яка дорiвнює кiлькостi теплоти, що необхiдна для нагрiву тiла на 10. А якщо нагрiвати одиницю маси речовини, то говорять про питому теплоємнiсть "с":
Питома теплоємність - це величина, яка дорiвнює кiлькостi теплоти, яка необхiдна для нагрiвання одиницi маси тiла на 10. А якщо нагрiвати 1 моль речовини
Порiвняння (5) i (6) дасть нам такий зв`язок:
Залежно вiд умов нагрiву розрiзняють теплоємностi при сталому тиску та об'ємі. Напишемо рiвняння Майера, яке показує, що молярна теплоємнiсть при сталому тискові більша, ніж молярна теплоємність при сталому об'ємі на величину унiверсальної газової сталої:
Ми знаємо, що для одного моля iдеального газу внутрiшня енергiя дорiвнює:
Формули (9) показують, що згiдно з основним положенням молекулярно-кінетичної теорiї молярнi теплоємностi незалежать вiд природи газу, а визначаються тiлькi числом ступеныв вiльностi молекули. А питомi теплоємностi з урахуванням (7) будуть мати вигляд:
5. Процес, який проходить у газовi без теплообмiну iз зовнiшнiм середовищем, має назву адiабатичного (
Фiзичний змiст: Робота звершується за рахунок зменшення внутрiшньої енергiї системи. Вiн описується рiвнянням Пуассона:
6. Ранiше ми дали визначення термодинамiчного процесу взагалi. Круговий процес (цикл) - це такий процес, при якому термодинамічна система, виходячи з початкового стану, проходить ряд промiжних i повертається знову в початковий стан. Коловi процеси лежать в основi роботи всiх теплових двигунiв, тому вивчення властивостей рiзних колових процесiв - одне з наважливiших завдань термодинаміки. Коловий процес оборотний, якщо пiсля його завершення система повертається у початковий стан разом з оточуючими її тiлами. Необхiдною та достатньою умовою проходження цього процесу є його рiвноважнiсть, тому для оборотного процесу Процес, при якому система не повертається в початковий стан, називається необоротним.
P I
Нехай газ знаходиться у цилiндрi пiд поршнем у станi I (Р1,V1,T1). Надамо газу теплоту Q1. Вiн розшириться i перейде у стан II (P2,V2,T2). Якщо вiдвести (забрати) у системи теплоту Q2, то це буде означати, що зовнiшнi сили виконали роботу А=Q1-Q2 над системою, внаслiдок чого газ стиснеться i перейде у стан I. Тобто система буде виконувати роботу за рахунок придбаної та вiдданої кiлькостi теплоти.
Перiодично дiючий двигун, який виконує роботу за рахунок рiзницi придбаної та вiдданоє кiлькостi теплоти, називається тепловим двигуном.
- коефiцiєнт корисної дiї теплового двигуна.
Якщо маємо проходження процесу по оборотному циклу, то слiд говорити про холодильну машину, для якої маємо:
Характерною особливiстю її є те, що розширення газу вiдбувається при нижчiй температурі, нiж нагрiвання. нагрівач Т1 нагрівач Т1
Q1 Q1
A робоче A робоче
Q2 Q2
холодильник Т2 холодильник Т2 Робота виконується Робота виконується газом над газом
7. Французький фiзик-iнженер Карно встановив, що максимальним ККД буде володiти iдеальна теплова машина, яка працює по замкненому циклу, котрий складається з двох адiабат та двох iзотерм. Умова iдеальної теплової машини: 1) стiнки поршня теплоiзольованi ( 2) дно поршня - iдеальний провiдник теплоти (Т = const); 3) нехтуємо силами тертя
- формула Карно. Т1,Т2 - абсолютнi температури нагрiвача та холодильника. Iз (14) видно, що Iз (14) випливає незалежнiсть ККД Карно вiд природи робочого тiла.
8. Коли застосувати найзагальнiший закон збереження та перетворення енергiї стосовно теплових процесiв, то перший початок термодинамiки не дозволяє встановити напрямок їх протiкання. Це визначається другим початком термодинаміки.
Його формулювання: І. Клаузiуса:
Неможливi такi процеси, єдиним i кiнцевим результатом яких був би перехiд теплоти вiд менш нагрiтого тiла до бiльш нагрiтого.
ІІ. Кельвiна:
Неможливий круговий процес, єдиним результатом якого є перетворення всiєї теплоти, одержаної вiд нагрiвача, в еквiвалентну їй роботу.
ІІІ. Вiчний двiгун другого роду неможливий.
Тепловий двигун, який працює тiльки за рахунок охолодження теплового резервуара, називається вiчним двигуном другого роду.
Другий початок термодинаміки вказує на нерiвнозначнiсть двох форм передачi енергiї - теплоти та роботи. Маємо оборотний цикл Карно:
Уведемо величину -
Перетворимо (15) в таке:
(15а) означає, що величина
Визначення: Функцiю стану системи, диференціал якої рівний приведеній теплотi, називають ентропiєю.
Для оборотного процесу ми мали формулу (15а), а з урахуванням необоротностi (не виконуються обмеження Карно),
- нерiвнiсть Клаузiуса (математичний вираз другого початку термодинаміки).
Можна довести, що в iзольованiй замкненiй системi при здійсненні оборотного циклу ентропiя залишається сталою (dS = 0), S = const. А при звершеннi необоротного циклу вона зростає (
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.250.223 (0.23 с.) |
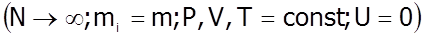
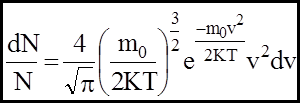 (1)
(1)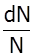 - імовірність того, що швидкості молекул розташовані в інтервалі від v до v + dv при даній температурі Т.
- імовірність того, що швидкості молекул розташовані в інтервалі від v до v + dv при даній температурі Т. Т1
Т1

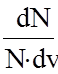
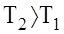






 v
v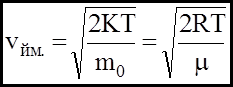 (2)
(2)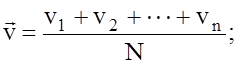
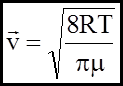 (3)
(3)
 =const, T=const.
=const, T=const.
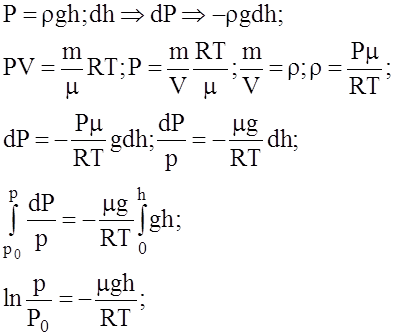
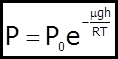 (4)
(4)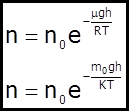 (5)
(5)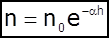
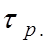 ).
).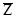 .
.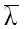 .
.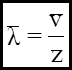 (6)
(6)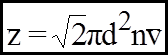 (7)
(7)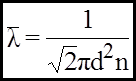 (8)
(8)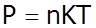 ,
, 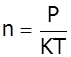 , то
, то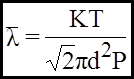 (8а)
(8а)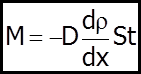 (9)
(9)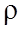 , прямо пропорцiйна градiєнту густини
, прямо пропорцiйна градiєнту густини 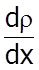 , площi S та часу t.
, площi S та часу t.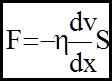 (10)
(10)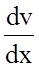
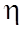 - коефiцiєнт в`язкостi (динамiчна в`язкiсть).
- коефiцiєнт в`язкостi (динамiчна в`язкiсть).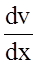 .
.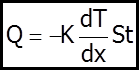 (11)
(11)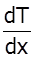 , площi S та часу t.
, площi S та часу t.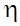 , К i мiкрохарактеристиками теплового руху молекул:
, К i мiкрохарактеристиками теплового руху молекул: 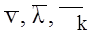
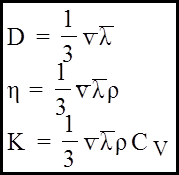 (12)
(12)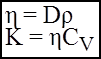
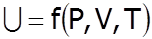 для даної маси.
для даної маси.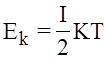 ;
;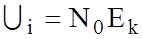 ;
; ;
; 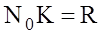 ;
;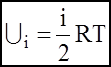 - внутрiшня енергiя одного моля iдеального газу.
- внутрiшня енергiя одного моля iдеального газу.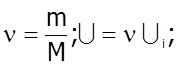
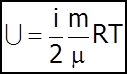 - внутрiшня енергiя iдеального газу.
- внутрiшня енергiя iдеального газу.


































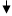 газ
газ 
 (2)
(2)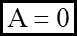
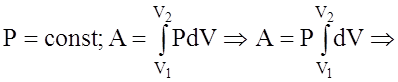
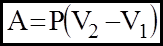
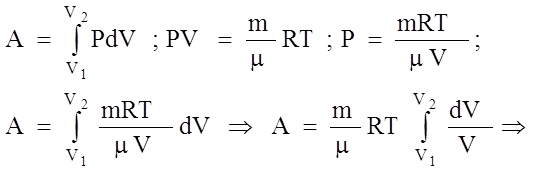
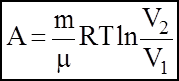
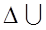 та на виконання цiєю системою роботи А проти зовнiшних сил.
та на виконання цiєю системою роботи А проти зовнiшних сил.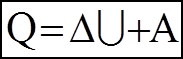 (3)
(3)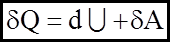 (3а)
(3а)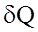 i
i 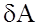 - неповнi диференцiали;
- неповнi диференцiали;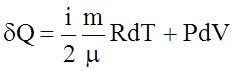
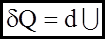 ;
;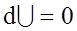 ;
; 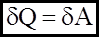 ;
;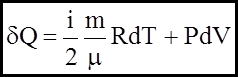 .
.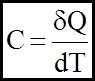 (4)
(4)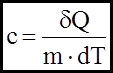 (5)
(5)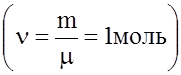 , то треба ввести поняття молярної теплоємностi "
, то треба ввести поняття молярної теплоємностi " 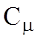 ":
":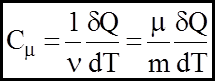 (6)
(6)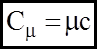 (7)
(7)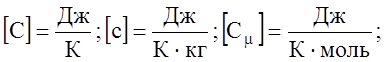
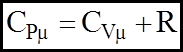 (8)
(8)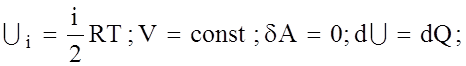 тоді:
тоді: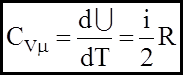 (9a)
(9a)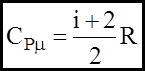 (9б)
(9б)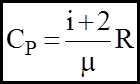 (10a)
(10a)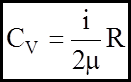 (10б)
(10б)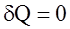 ).
).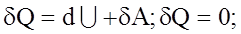 тоді:
тоді: 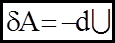 - із першого початку термодинамiки.
- із першого початку термодинамiки.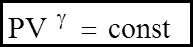 (11)
(11)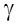 - показник адiабати;
- показник адiабати;  .
.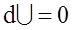 .
.

 Q1
Q1
 Q2
Q2 II
II V
V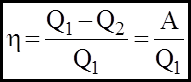 (12)
(12)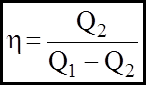 (13)
(13) 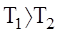




 тіло тіло
тіло тіло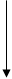
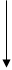


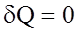 );
); .
.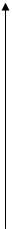 P
P

 1
1
 2
2


 3
3
 4
4 V
V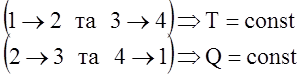
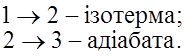
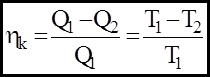 (14)
(14)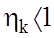 ; але взагалi
; але взагалi 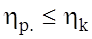 .
.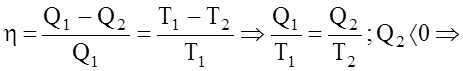
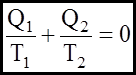 (15)
(15)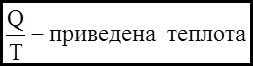
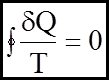 (15a)
(15a)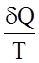 не залежить вiд характеру процесу, а залежить лише вiд початкового та кiнцевого станiв.
не залежить вiд характеру процесу, а залежить лише вiд початкового та кiнцевого станiв.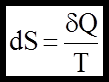 (16)
(16)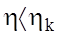 , тодi (15а) перейде в наступне:
, тодi (15а) перейде в наступне: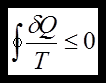 (17)
(17)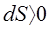 ).
).


