
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трохи про консервативні системиСтр 1 из 13Следующая ⇒
5. Перейдемо від поступального руху до обертального. Математично це зробимо, помноживши (1) на радіус-вектор будь-якої матеріальної точки:
Можна показати, що не порушивши строгість викладення математично, можна замінити цей вираз так:
Введемо поняття моменту імпульсу
Введемо суму моментів імпульсу:
відносно точки 0.
відносно точки 0. Тоді запишемо закон обертального руху:
Швидкість зміни момента імпульсу Відносно нерухомої точки О дорівнює результуючому моменту сил А якщо перейти від обертання відносно нерухомої точки до обертання відносно нерухомої вісі, то проекції
Z
X
Це математичний запис основного закону динаміки обертального руху при обертанні твердого тіла відносно нерухомої осі.
6. Ми ввели момент імпульсу Але при обертанні навколо нерухомої осі Оскільки обертання кожної точки здійснюється з кутовою швидкістю
нерухомої осі (за визначенням).
- момент інерції твердого тіла відносно нерухомої осі.
- момент імпульсу твердого тіла відносно нерухомої осі.
- це ще один запис основного закону динаміки обертального руху. Нерухома вiсь обертання може проходити як через центр iнерцiї абсолютно твердого тiла, так i не через нього. В таких випадках для пiдрахування моменту iнерцiї використовують теорему Штейнера:
d
Момент iнерцiї абсолютно твердого тiла вiдносно осi Z', яка не проходить через центр iнерцiї, дорiвнює моменту iнерцiї Iz вiдносно паралельної осi, яка проходить через центр iнерцiї абсолютно твердого тiла плюс добуток маси абсолютно твердого тiла на квадрат вiдстанi d мiж цими паралельними осями.
7. Для зовнішньої системи маємо:
Закон збереження моменту імпульсу:
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.216.163 (0.013 с.) |
 Якщо в замкненій системі діють консервативні сили, то такі системи називаються консервативними. Їх особливість полягає в тому, що в них відсутнє перетворення механічної енргії в інші види енергії. А якщо ця умова не виконується, то такі системи – дисипативні. В цьому випадкові механічна енергія перетворюється в інші види енергії (сили тертя та інше).
Якщо в замкненій системі діють консервативні сили, то такі системи називаються консервативними. Їх особливість полягає в тому, що в них відсутнє перетворення механічної енргії в інші види енергії. А якщо ця умова не виконується, то такі системи – дисипативні. В цьому випадкові механічна енергія перетворюється в інші види енергії (сили тертя та інше).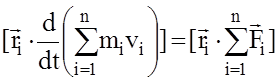 .
.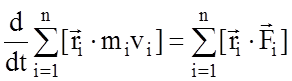
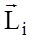 і момент сили
і момент сили  довільної матеріальної точки відносно будь-якої точки О у твердому тілі.
довільної матеріальної точки відносно будь-якої точки О у твердому тілі.
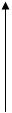
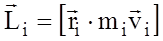
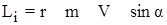



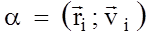






 mi
mi


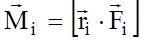



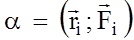









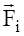

 mi
mi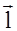 – плече сили – це перпендикуляр, проведений від точки до напрямку, вздовж якого діє сила.
– плече сили – це перпендикуляр, проведений від точки до напрямку, вздовж якого діє сила.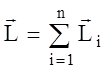 - момент імпульсу абсолютно твердого тіла
- момент імпульсу абсолютно твердого тіла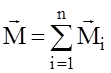 - момент сили абсолютно твердого тіла
- момент сили абсолютно твердого тіла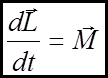 (14)
(14)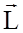
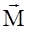 усіх зовнішніх сил.
усіх зовнішніх сил.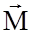 на вісі Х та У взаємно компенсуються. Тоді (14) перейде в слідуюче:
на вісі Х та У взаємно компенсуються. Тоді (14) перейде в слідуюче: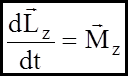 (15)
(15)





 Mz M
Mz M
 Y
Y
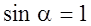 .
. , то
, то
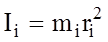 - момент інерції матеріальної точки відносно
- момент інерції матеріальної точки відносно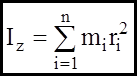 (16)
(16)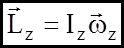 (17)
(17)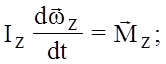
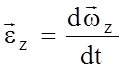 - кутове прискорення твердого тіла.
- кутове прискорення твердого тіла.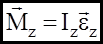 (18)
(18)

 Z ' Z
Z ' Z








 c
c

 C
C (19)
(19)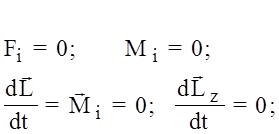
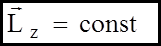 (20)
(20)


