
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Це I є формулюванням другого початку термодинаміки, або
Якщо система переходить iз стану А в стан В, то ентропiя стану А менше від ентропiї стану В (
У теплоiзольованих системах усi реальнi процеси протiкають у напрямі збiльшення ентропiї.
1) iзобаричний (Р = const):
2) iзотермiчний (Т = соnst):
3) iзохоричний (V = const):
ЛЕКЦІЯ X ТЕМА: ТВЕРДІ ТІЛА ТА РІДИНИ ПЛАН
1. Молекулярна будова рiдини. Поверхневий натяг. 2. Явище змочування. Формула Лапласа. 3. Капiлярнi явища. Формула Жюрена. 4. Твердi тiла та їх будова. Закон Дюлонга i Птi.
1. Розглянемо характер мiжмолекулярної взаємодiї у рiдинi.
Рiвнодiюча всiх сил, які дiють на молекулу у серединi рiдини, дорiвнює 0. На молекулу в поверхневому шарi дiє рiвнодiюча сила, яка направлена у середину рiдини (оскільки ця молекула взаємодiє з бiльшою кiлькістю молекул у рiдинi та з меншою - над поверхнею).
Тому при переходi молекул із глибини рiдини у поверхневий шар необхiдно витратити роботу проти сил, дiючих у поверхневому шарi.
Унаслiдок цього поверхневий шар рiдини буде мати додаткову енергiю при Т = const. В умовах рівноваги система завжди намагається мати найменшу потенціальну енергію, тому рідина буде приймати форму, відповідну мінімумові потенціальної енергії.
Сили, дiючi на поверхнi рiдини, якi прагнуть зменшити величину її поверхнi, називають силами поверхневого натягу.
Для кiлькiсної оцiнки цих сил уводять поняття коефіцієнта поверхневого натягу
l - довжина граничної лiнiї.
2. У випадкові контакту рiдини з твердим тiлом можуть простежуватися два наслiдки ефекту взаємодiї: а) змочування; б) незмочування.
незмочування:
повне змочування:
Ефект змочування або незмочування поверхнi твердого тiла рiдиною приводить до викривлення поверхнi рiдини, а будь-яка викривлена поверхня чинить на рiдину додатковий тиск
Кiлькiсну оцiнку величини
- формула Лапласа.
R1, R2 - радiуси кривизни поверхнi у двох взаємно перпендикулярних перерiзах, проведених через одну й ту ж саму точку.
Для сферичної поверхнi R1 = R2:
3. Ефект змочування або незмочування визначає поведiнку рiдини у капiлярах:
змочування приводить до пiднiмання рiдини в капiлярi; незмочування – до опускання.
Змiна рiвня рiдини h у капiлярах визначається формулою Жюрена:
r - радіус капіляра;
4. Визначальна особливiсть твердих тiл - наявнiсть кристалiчної решiтки, у вузлах якої частинки звершують тепловий (коливальний) рух.
Тверді тiла подiляються на: а) монокристали, б) полiкристали. Монокристали - це такі тверді тiла, для яких характерна єдина кристалiчна решiтка зі сталими кутами мiж гранями.
Полiкристали – це сукупнiсть великої кiлькостi хаотичноорiєнтованих малих кристалічних зерен. Залежно вiд типу частинок у вузлах решiтки та характеру сил взаємодiї мiж цими частинками, кристали розподiляються на чотири основнi типи:
1) іоннi (KCl, NaCl), 2) aтомнi, 3) металеві,
4) молекулярнi.
Iоннi - у вузлах решiтки є чергування позитивних та негативних iонiв. Атомнi - у вузлах кристалічної решiтки знаходяться нейтральнi атоми.
Металiчнi - у вузлах знаходяться позитивнi iони, а в промiжках мiж вузлами iснує електронний газ. Це дуже добрi провiдники електрики (Cu, Fe).
Молекулярнi - у вузлах кристалічної решiтки знаходяться нейтральні молекули.
Коротко спинимось на теплоємностi твердих тiл. Закон Дюлонга i Птi констатує:
Молярна теплоємнiсть усiх хімічних простих кристалiв дорiвнює 3R при високих температурах.
Т3 (Дебая)
~ 300 K Т,К Лекція XI ТЕМА: ЕЛЕКТРОСТАТИКА
ПЛАН 1. Електричний заряд, закон Кулона. 2. Напруженість електричного поля. Принцип суперпозиції. 3. Потік вектора напруженості. Теорема Гауса. 4. Робота сил електричного поля. Циркуляція вектора 5. Потенціал. Зв’язок між 6. Провідники в електричному полі. 7. Електроємність. 8. Енергія конденсатора, густина енергії електричного поля.
1. Як відомо, в природі існують два види електричних зарядів: а) позитивні “ +”, б) негативні “ - ”. Звичайно, однойменні заряди відштовхуються, а різнойменні притягуються. Найменшою за масою спокою частинкою, яка має негативний елементарний заряд, є електрон
е = 1,6 × 10-19 Кл; me=9.1 ×10-31 кг Електричний заряд тіл квантується, тобто приймає ряд дискретних значень (переривчастих).
q = ± ne (n = 1, 2, 3 …) (1) Тіло приймає або віддає тільки величини зарядів, які кратні елементарному. Експериментально було встановлено, що в ізольованій системі алгебраїчна сума зарядів зберігається
Алгебраїчна сума електричних зарядів тіл або частинок, які створюють електрично ізольовану систему, не змінюється при будь-яких процесах, які відбуваються в цій системі (фундаментальний закон природи). Заряди взаємодіють. Закон цієї взаємодії був установлений у 1785 р. Кулоном: сила взаємодії двох точкових зарядів для однорідного, ізотропного та нескінченного середовища прямо пропорційна добутку величин цих зарядів і обернено пропорційна квадрату відстані між ними.
F= k× (q1 q2 / r2), (3)
k- коефіцієнт пропорційності, який залежить від вибору системи одиниць та від властивостей середовища. Електричні властивості середовища характеризуються діелектричною проникністю e, яка показує, у скільки разів сила взаємодії зарядів у вакуумі F0 більша, ніж така ж сила F у середовищі на тій же відстані.
e = F0 / F (4)
Тому для однорідного, ізотропного та нескінченного середовища закон Кулона має вигляд: F= k× (q1 q2 / r2); (5) Для вакууму e = 1; k = 9 ×109 Н×м2 / Кл2
F = q1q2 /4pe0r2 (5a)
2. Оскільки заряджені тіла взаємодіють, то повинно існувати таке середовище, яке передає цю взаємодію. Матеріальне середовище, оточуюче будь-яке нерухоме заряджене тіло, називається електростатичним полем.
Механізм взаємодії
Поля не взаємодіють, а заряджене тіло створює навколо себе поле, яке діє на інше заряджене тіло із силою F. Для будь-якої точки поля можна ввести його силову характеристику - напруженість, яка чисельно дорівнює силі F, діючій з боку електричного поля на одиничний позитивний точковий заряд, унесений до цієї точки поля:
З урахуванням (5) і (6) маємо:
EA = q /4pe0r2; (7)
- напруженість електростатичного поля, створеного у точці А точковим зарядом q. [ Е ] = Н/Кл =В/м. Якщо електростатичне поле буде створене не одним точковим зарядом, а системою таких зарядів, то напруженість результуючого поля буде дорівнюватиме геометричній сумі напруженостей, створених кожним зарядом окремо. Це є принцип суперпозиції.
Формули (6), (7), (8) дають нам аналітичне зображення електростатичного поля. Існує також графічне зображення електричного поля за допомогою силових ліній.
Потоком (елементарними потоком) вектора напруженості через поверхню dS, проведену в полі, є величина, яка визначається скалярним добутком
d Фе = (
Повний потік для будь-якої замкненої поверхні S:
Теорема Остроградського-Гауса стверджує: потік вектора
Для середовища з проникністю e вираз (10) переходить у наступний:
4. Елементарна робота dA, яка виконується силою
A=(q0q /4p e0 e)(1/r1- 1/r2) (11) З (11) видно, що робота не залежить від форми шляху, а залежить тільки від початкового та кінцевого положеня точок. Висновок: сили електростатичного поля консервативні, а саме поле потенціальне. dA = q0 (
A = q0 Із формули (11) видно, що робота електричного поля по замкненому контуру (r1= r2 ) дорівнює нулю. Таким чином, із визначення циркуляції виходить, що вона дорівнює нулю. Якщо циркуляція вектора будь-якого силового поля дорівнює 0, то як наслідок силові лінії такого поля не замкнені.
5. Із розділу механіки відомо, що робота консервативних сил виконується за рахунок змін потенціальної енергії;
A = - DWn = - (Wn(2) - Wn(1)) = Wn(1) - Wn(2) (12) Wn – потенціальна енергія заряду.
Wn(2) – потенціальна енергія заряду в точці 2. Wn(1) – потенціальна енергія заряду в точці 1.
Із рівняння (12) і (11)
Wn = qq0 /(4p e0 e r) + c; c = 0 (r ®
Wn = qq0 /(4p e0 e r); (13) Потенціалом j даної точки поля називається відношення потенціальної енергії Wn заряду q0 у даній точці до величини цього заряду.
j = Wn / q0; (14)
Із (14) видно, що потенціал — це енергетична характеристика даної точки поля. Знайдемо зв’язок між
dA = q0 E dl; dA = - d Wn; dA = - q0 dj; q0Edl = - q0 dj;
El = - (dj /dl);
Напруженість поля в даній точці дорівнює градієнтові потенціалу, взятому з протилежним знаком. Будь-яка точка електричного поля характеризується як векторною, так і скалярною величинами (
6. Якщо помістити провідник у зовнішнє електричне поле, то вільні заряди (наприклад- d електрони у металі) перерозподіляться такими чином, що напруженість електричного поля у середині провідника буде дорівнювати нулю.
Е = 0; (dj /dl) = 0; j = const, як у середині провідника, так і на його поверхні, тобто весь об’єм провідника, можна вважати еквіпотенціальним, а напруженість електричного поля біля поверхні завжди буде спрямована по нормалі до поверхні у даній точці. Якщо надати провіднику додатковий електричний заряд, то нескомпенсовані заряди розмістяться тільки на поверхні провідника. Ця властивість застосовується для електростатичного екранування від зовнішніх електричних полів. Можна показати, що напруженість електростатичного поля поблизу поверхні провідника прямо пропорційна поверхневій густині заряду s:
s = q / S; Еn = s / e0 e; (16)
7. Як показує досвід, при нанесенні на відокремлений провідник заряду для однакових провідників зі зростанням величини заряду q буде зростати і потенціал цього провідника j. Тому для відокремленого провідника: j = (1/С) q; (17) де С – ємність відокремленого провідника
С = q / j; (18) [ C ] = Кл / В = Ф.
Ємність залежить від геометричної будови провідника (його форми та лінійних розмірів) ті діелектричної проникності середовища, в якому він знаходиться. Для сфери: С = 4p e0 e R, де R – радіус сфери.
Конденсатор – це система, що являє собою два провідники, які розділені шаром діелектрика.
С = e0 e S / d; (19)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.83.97 (0.214 с.) |
 ).
).
 ;
; ;
; .
.






















 Fp.= 0
Fp.= 0
 .
. iзотермiчного утворення поверхнi рiдини до площi цiєї поверхнi
iзотермiчного утворення поверхнi рiдини до площi цiєї поверхнi  .
. (1)
(1) (2)
(2)
 Hg (ртуть)
Hg (ртуть)



 Н2О (вода)
Н2О (вода)


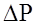 порiвняно з таким у випадкові контакту рiдини з плоскою поверхнею.
порiвняно з таким у випадкові контакту рiдини з плоскою поверхнею. (3)
(3)




























 (4)
(4) - густина рідини;
- густина рідини; - коефіцієнт поверхневого натягу;
- коефіцієнт поверхневого натягу;

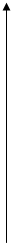
 Закон Дюлонга і Пті
Закон Дюлонга і Пті



 3R
3R


 .
. та j.
та j. (2)
(2) .
.

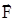 / q (6)
/ q (6)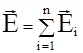 . (8)
. (8)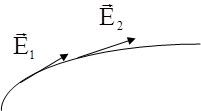 Силова лінія – це уявна крива, у кожній точці якої вектор поля
Силова лінія – це уявна крива, у кожній точці якої вектор поля 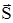 )
) (9)
(9)
 eлектростатичного поля у вакуумі через будь-яку замкнену поверхню дорівнює алгебраїчній сумі електричних зарядів, які оточені цією поверхнею, та поділену на e0.
eлектростатичного поля у вакуумі через будь-яку замкнену поверхню дорівнює алгебраїчній сумі електричних зарядів, які оточені цією поверхнею, та поділену на e0. (10)
(10) (10a)
(10a)

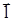 ) =q0Edl ×cos a = q0 E dr
Робота, яку виконує електричне поле при переміщенні заряду q0 з точки 1 (r1) у точку 2 (r2)
) =q0Edl ×cos a = q0 E dr
Робота, яку виконує електричне поле при переміщенні заряду q0 з точки 1 (r1) у точку 2 (r2)
 або
або
 (
(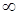 )
) ; (15)
; (15) j = - grad j;
j = - grad j;


