
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: електричне поле в діелектриках
план 1. Полярні та неполярні діелектрики. Електричний диполь. 2. Вектор поляризації. Електричне поле у середині діелектрика. 3. Теорема Гауса для діелектриків. Густина енергії електростатичного поля.
1. За електричними властивостями всі тіла умовно можна розділити на провідники, діелектрики та напівпровідники. Взагалі пояснення цієї різниці має зміст тільки з урахуванням квантових особливостей на основі зонної теорії твердих тіл. Однак на якісному рівні цю різницю можна ще пояснити на основі різної рухомості електричних зарядів. У провідниках існують вільні заряди, які здатні переміщуватися у межах речовини, наприклад, вільні електрони у металах. У діелектриків вільних зарядів немає. В них існують зв’язані заряди, які розташовані у вузлах кристалічної решітки. Однак молекули володіють електричними властивостями, й, у першому наближенні молекулу можна розглядати як електричний диполь. Електричний диполь - це система, яка складається з двох однакових зарядів протилежного знаку, які знаходяться на малій відстані.
Електричний момент диполя
Діелектрики підрозділяються на полярні та неполярні. Неполярні молекули (H2, O2, N2...) мають симетричну будову, а центри тяжіння Å зарядів та Θ зарядів збігаються внаслідок симетричності електронних орбіт. Тому для них електричний момент дорівнює нулю у відсутності зовнішнього електричного поля.
( У полярних діелектриках молекули (CO2, SO3, NH3,...) мають асиметричну будову. Тому для них
діелектрика має результуючий електричний момент, рівний нулю.
å
При розміщенні будь-якого діелектрика у зовнішньому електричному полі весь об”єм діелектрика дістає результуючий електричний момент, не рівний нулю Це явище зветься поляризацією діелектрика. У неполярних діелектриках - поляризація деформаційна, оскільки вона пов’язана з деформацією електронних орбіт. У полярних діелектриках вона орієнтаційна, бо пов’язана з орієнтацією діполей усього об’єму діелектрика у зовнішньому електричному полі.
2.
Для кількісної характеристики явища поляризації вводиться векторна величина - вектор поляризації
де V - об’єм усього діелектрика, а
Фізичний зміст Експериментально було встановлено, що в малих електричних полях для однорідних ізотропних діелектриків існує така залежність:
де À - діелектрична сприйнятливість.
Помістимо діелектрик у зовнішнє електричне поле:
Можна показати, що поверхнева густина зв’язаних зарядів дорівнює Рn
s = Pn; E = s / e0 Вектор
e = F0 / F = E0 / E
Фізичний зміст e - характеристикавластивості діелектрика поляризуватися у зовнішньому електричному полі. e1
e2
На межі поділу двох діелектриків із різними e дві складові (нормальна та тангенційна) вектора ( Тому для зручності у розрахунку електричних полів уводять вектор D - вектор електростатичної індукції, нормальна складова якої не змінюється при переході від середовища з e1 до середовища зe2 (Dn1 = Dn2).
у вакуумі e = 1, якщо у середовищі, то
у вакуумі Це основне рівняння електростатики діелектриків. Із (7) видно, що
3. Для електричного поля у вакуумі теорема Гауса мала вигляд
а для середовища
Тому аналогічно для поля в діелектрику маємо: для вільних зарядів:
потік
w = e0 e E2 / 2;
Об”ємна густина енергії електричного поля:
w =
ЛЕКЦІЯ Х IV ТЕМА: МАГНІТНЕ ПОЛЕ ПЛАН 1. Магнітне поле. Сила Ампера. 2. Сила Лоренца. 3. Закон Біо-Савара-Лапласа. Принцип суперпозиції. Приклади розрахунків полів. 4. Рамка зі струмом у магнітному полі. 5. Закон повного струму. 6. Магнітний потік. Теорема Гауса. 7. Робота з переміщення провідника зі струмом у магнітному полі.
1. За відсутності струму провідники не взаємодіють. При пропусканні струму в однаковому напрямку вони будуть притягуватися. Тобто ми спостерігаємо факт взаємодії провідників унаслідок протікання через них струму. Оскільки цю взаємодію ми спостерігаємо об’єктивно, то повинно існувати таке матеріальне середовище, яке буде передавати цю взаємодію. Це матеріальне середовище має назву - магнітне поле. Магнітне поле - це матеріальне середовище, яке оточує провідник зі струмом та рухомі електричні заряди. Головна характеристика магнітного поля - вектор магнітної індукції Його напрямок збігається з силою, яка діє на відповідний полюс магнітної стрілки, що поміщена в цю точку поля. Опис магнітного поля за допомогою вектора Окрім цього, існує графічний засіб описання - за допомогою силових ліній. Силова лінія - це така уявна лінія, у кожній точці якої Правило свердлика Якщо поступальний рух свердлика вказує на напрямок струму, то обертальний рух його рукоятки вказує на напрямок силових ліній. Числове значення сили, діючої на провідник зі струмом у магнітному полі, встановив Ампер, який показав, що для однорідного магнітного поля чисельне значення цієї сили визначається за формулою
d a = (B,Ùdl)
a
d
Вектор магнітної індукції чисельно дорівнює максимальній силі, яка діє на провідник одиничної довжини зі струмом, рівним одному амперу.
[ B ] = Tл (тесла); Tл = Н /(А × м)
2. Магнітне поле повинне діяти не тільки на провідник зі струмом, але й на рухомий заряд. d j = q n J = q v n S; n = N / V; Idl = q v n Sdl = q v dV; Sdl = dV; n Sdl = dN;
dF = q dN [
Із формули (3) випливає, що
У загальному випадкові:
3. Закон Біо - Савара - Лапласа Досліди показали, що: 1) Індукція магнітного поля прямо пропорційна силі струму в провідникові В ~ І. 2) В залежить від форми та розмірів провідника зі струмом у магнітному полі. B = f (форма і розміри) 3) У даній точці магнітного поля що залежить від розміщення цієї точці відносно провідника зі струмом. Ці три основні наслідки стимулювали появу загального закону, який би дав можливість обчислювати
d
де d
к - коефіцієнт пропорційності, який визначається дослідним шляхом. dB - елементарна індукція. Вона перпендикулярна площині, в якій лежать вектори d Для однорідного та ізотропного середовища:
m0 = 4p ×10-7 Гн / м m = 1 (для вакууму) dB = (mm0І / 4pr2) dl sina (5a) Закон Біо-Савара-Лапласа дає можливість знайти вектор магнітної індукції для струму, який тече в провідникові кінцевих розмірів, завдяки принципу суперпозиції
n
i = 1
де n - загальне число ділянок, на які розбито провідник. Якщо n ® ¥; å ®
а) Для відрізка провідника: B = mm0І / 4pr0 (cosa1 - cosa2 )
б) Для нескінченно довгого провідника a1 ® 0; a2 ® p cos a1 - cos a2 = 2 B = mm0І / 2pr0.
в) B = mm0І / 2R – у центрі колового провідника
г) У середині соленоїда
d << l B = mm0І, n = N / де n - число витків.
a
Магнітний момент контуру зі струмом:
M = рm × B × sina;
B
0 рm
5. Закон повного струму. Як нам відомо, циркуляція вектора напруженості електричного поля по замкненому контуру дорівнює нулю. Це говорить про те, що електричне поле є потенційним.
Для магнітного поля виділяємо контур
І1
Циркуляція вектора
6. Магнітний потік через поверхню площиною dS дорівнює добутку модуля вектора
dФm = B × dS cosa; B dФm = B × dS; a n a = (nÙ,B) a = 0о (
В електродинаміці доводиться теорема Остроградського - Гауса: магнітний потік через будь-яку замкнену поверхню дорівнює нулю.
Фізичний зміст формули: у природі не існують магнітні заряди, тому силові лінії магнітного поля завжди замкнені і магнітне поле не потенціальне, а вихрове, (на противагу електростатичному полю).
7. Оскільки на провідник зі струмом у магнітному полі буде діяти Fамп, то він буде переміщуватись, а ця сила діє з боку магнітного поля, виконує роботу з переміщення провідника зі струмом у магнітному полі.
ЛЕКЦІЯ XV
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.67.251 (0.11 с.) |
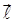
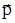
 · ·
· · (1)
(1) = 0).
= 0).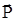 .
.








 +s -s
E
+s -s
E
 ;
;
 = e0
= e0 
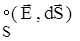 = 1/e0
= 1/e0  ,
,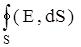 = 1 / ee0
= 1 / ee0  дорівнює сумі всіх вільних зарядів.
дорівнює сумі всіх вільних зарядів. .
. = I d
= I d  ×
×  dl
dl dF
B
dl
dF
B
dl
 (2)
(2)
 ;
;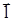 ×
×  ], (5)
], (5)

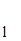




 ,
,  = 1 (7)
= 1 (7)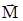 = [
= [ 


 a
a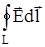 = 0.
= 0. І2
І2 (9)
(9) дорівнює добутку магніт-ної сталої m0 на алгебраїчну суму всіх струмів, які охоплені цим контуром. Це твердження є законом повного струму.
дорівнює добутку магніт-ної сталої m0 на алгебраїчну суму всіх струмів, які охоплені цим контуром. Це твердження є законом повного струму.
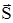 ) = dФm (10)
) = dФm (10)





