
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производственная функция. Свойства производственных функций. Основные типы производственных функций.Содержание книги
Поиск на нашем сайте
Процесс произв-ва – взаимодействие факторов произ-ва, завершающееся созданием экон-го блага. Комбинация факторов произ-ва, необходимая для получения блага при данном технологическом уровне произ-ва. Кажд способ произ-ва м.б. охарактеризован строго определенным набором факторов, позвол-щим получить единицу экон-го блага при заданном уровне технологии. Теория произ-ва изучает, прежде всего, соотношение м/д кол-вом применяемых факторов произ-ва и объемом выпуска экон-ких благ. Взаимоотнош-е кол-ва использ-мых факторов произ-ва и макс-но возможного выпуска экон-го блага описывается произ-ной ф-цией. Произ-ная ф-ция строится для опред-ной технологии и описывает мн-во технически эффектив-ых способов произ-ва. Способ произ-ва А явл-ся технически эффектив-ым способом по сравнению со способом В, если предпол-ет испол-ние хотя бы одного фактора произ-ва в меньшем, а всех остальных – не в большем кол-ве, чем способ В. Фирма, ведущая себя как рацион-ный субъект, использует только технически эффективные способы произ-ва. Из мн-ва технически эфф-ных способов произ-ва важно выбрать экон-ки эфф-ное сочетание факторов произ-ва, т.е. такой способ произ-ва, при кот фирма получает максим-ную эфф-сть от применяемых экон-ких рес-сов, мин-руя свои экон-кие изд-ки. Предположим, что в произ-ве испол-ся труд (L) и капитал (К), а получаемый макс-ный объем экон-го блага – Q, тогда произ-ную ф-цию в общем виде можно представить так
Каждая изокванта ассоциируется с конкретным объемом выпуска продукции. Для того чтобы отразить связь между технически эфф-ными способами произ-ва и кажд конкретным объемом произ-ва, следует рассм-ть не отдельно взятую изокванту, а целую систему изоквант. Карта изоквант отражает сов-ть всех изоквант, кажд из кот представляет максимальный выпуск экон-го блага при испол-нии опред-ного сочетания факторов произ-ва (см рис 1). У всех произ-ых ф-ций имеются общие св-ва. 1. всегда сущ-ет предел для наращивания объема произ-ва, кот достижим путем увеличения затрат одного из рес-ов при прочих равных усл-ях. 2. сущ-ет опред-ная комплементарность факторов произ-ва, при том, что без сокращения объема произ-ва возможна определ-ная взаимозаменяемость данных факторов произ-ва (рис 2). Замещение одного фактора произ-ва другим в факторном наборе при сохранении пост-ным объема произ-ва м.б. охарактеризовано углом наклона касательной, проведенной к изокванте в данной точке. Наклон изокванты хар-ет предельную норму технич-го замещения, кот показывает от какого кол-ва капитала следует отказаться ради увеличения в факторном наборе труда на одну дополнит единицу при усл-вии неизмен-сти объма выпуска экон-го блага:
3. чем продолжительнее отрезок времени, тем значит-нее м.б. изменения в использ-нии факторов произ-ва. Т.е. фирма имеет большие возм-ти в принятии решений по произ-ву в долгосрочном периоде времени, чем в краткосрочном. Краткосрочн период – период времени, в течении кот хотя бы один фактор произ-ва не м.б. изменен. Поэтому изменить объем произ-ва возм-но только за счет более интенсивного испол-ния данного неизмен-го (пост-го) фактора произ-ва (рис 5). Движение способа А к В или С. Долгосрочн период – пер времени, достаточный для внесения измен-ий во все используемые фак-ры произ-ва с целью измен-нию объема произ-ва. (рис 5) увелич объема Q1 до Q2 путем измен-ия факторного набора А на набор В или D. Для линейн ф-ции характерна линейная завис-ть выпуска от затрат. Произ ф-ци К-Д выражает логарифм выпуска как линейную ф-цию логарифма затрат. Произ ф-ция затрат-выпуска есть одна из заданных пропорций, кот-ми для произ-ва одной единицы выпуска опред-ся кол-во затрат кажд вида. Произ ф-ция анализа произ-ной деят-ти обобщает произ-ную ф-цию затрат-выпуска на случай, когда сущ-ет р элементарных процессов, называемых активностями, кажд из кот может протекать при любой неотриц-ой интенсивности. Произ ф-ция с пост эластичностью замещения, для кот σ, эласт-ть замещения, равна Существует несколько подходов к тестированию регрессионных остатков на автокорреляцию. Во многих статистических пакетах решение задач по построению регрессии дополняется графическим представлением результатов моделирования. В том числе предоставляется возможность визуализации поведения отклонений во времени. Чаще других используется критерий Дарбина-Уотсона. В его основу положена простая идея, в соответсвии с которой, если корреляция случайной составляющей регрессии 1) модель, для которой возникает необходимость примения этого критерия должна содержать свободный член; 2) предполагается, что случайная составляющая модели 3) наблюдения, используемые для построения модели, имеют одинаковую периодичность, то есть в них нет пропусков; 4) критерий нельзя применять, если в регрессионной модели в число обясняющих переменных входит зависимая переменная с лагом в один период. Такое ограничение связано с тем, что распределение статистики d зависит не только от числа наблюдений, но и от значений самих регрессоров. А это означает, что тест перестает играть роль критерия в том смысле, что нельзя указать критическую область, которая позволяла бы принимтаь решение об отсутствии автокорреляции в тех случаях, когда в эту область попадают наблюдаемые значения статистики d.
В моделях, содержащих авторегрессионные члены, разработан критерий для обнаружения автокоррелированности остатков: Таким образом, статистика h легко вычисляется на основе данных оцененной регрессии (3). Единственная проблема, которая может возникнуть связана с тем, что вполне возможен случай, когда n
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.176 (0.011 с.) |

 Графич-ки произ-ную ф-цию можно выразить при помощи карты изоквант. Изокванта – это кривая, на кот расположены все комбинации факторов произ-ва, испол-ние кот позволяет достичь опред-го объема выпуска в физич выражении. Одно и то же кол-во продукции м.б. получено при различн сочетаниях труда и капитала. В том сл, когда при перечисленных комбинациях сохраняется неизмен-ым наибольший объем выпуска, то графич-ки данные сочетания факторов произ-ва можно представить точками, лежащими на на одной и той же изокванте. Т.о. изокванта показывает, что сущ-ет мн-во вариантов для произ-ва данного объема продукции. На рис 1 представлена изокванта, соответ-щая объему выпуска
Графич-ки произ-ную ф-цию можно выразить при помощи карты изоквант. Изокванта – это кривая, на кот расположены все комбинации факторов произ-ва, испол-ние кот позволяет достичь опред-го объема выпуска в физич выражении. Одно и то же кол-во продукции м.б. получено при различн сочетаниях труда и капитала. В том сл, когда при перечисленных комбинациях сохраняется неизмен-ым наибольший объем выпуска, то графич-ки данные сочетания факторов произ-ва можно представить точками, лежащими на на одной и той же изокванте. Т.о. изокванта показывает, что сущ-ет мн-во вариантов для произ-ва данного объема продукции. На рис 1 представлена изокванта, соответ-щая объему выпуска  . Точкой А обозначен высомеханизированный способ произ-ва, обеспеч-щий получение данного объема. Точкой D обозначен также технически эфф-ный способ произ-ва, но предполаг-щий получение того же объема
. Точкой А обозначен высомеханизированный способ произ-ва, обеспеч-щий получение данного объема. Точкой D обозначен также технически эфф-ный способ произ-ва, но предполаг-щий получение того же объема  . Для изоквант, вогнутых к началу координат, MRTS сокращ-ся по мере движения сверху вниз вдоль изокванты, что свидетельствует об органич-сти испол-ния любого фактора произ-ва при данном объеме испол-ния другого фактора произ-ва. В нашем сл речь идет о замещении капитала трудом, след-но, по мере данного замещения постеп-но сниж-ся производ-сть труда. Данное св-во проявляет себя и при движении вдоль изокванты в обратном направлении: снизу вверх, когда труд замещ-ся большим кол-вом капитала, при этом отдача от капитала тоже постеп-но будет снижаться. Это позволяет сделать вывод о том, что следует искать оптим-ое сочетание факторов произ-ва. Изокванты могут иметь разную конфигурацию, что связано со способ-тью произ-ных факторов замещать др друга в процессе произ-ва. Если факторы произ-ва выступают относит-но др др абсол-ными субститутами, то изокванта линейна, а MRTS предст соб неизменную величину, т.е. наклон изокванты неизменен. (рис 3) Если факторы произ-ва выступают абсол-но комплементарными относ-но др др, то изокванта принимает принцип-но иной вид (рис 4). Замещение одного фактора произ-ва другим нецелесообразно: труд и капитал комбинир-ся в единст-но возм-ом сочетании факторов произ-ва дл кажд дан-го объема произ-ва (А,В,С).
. Для изоквант, вогнутых к началу координат, MRTS сокращ-ся по мере движения сверху вниз вдоль изокванты, что свидетельствует об органич-сти испол-ния любого фактора произ-ва при данном объеме испол-ния другого фактора произ-ва. В нашем сл речь идет о замещении капитала трудом, след-но, по мере данного замещения постеп-но сниж-ся производ-сть труда. Данное св-во проявляет себя и при движении вдоль изокванты в обратном направлении: снизу вверх, когда труд замещ-ся большим кол-вом капитала, при этом отдача от капитала тоже постеп-но будет снижаться. Это позволяет сделать вывод о том, что следует искать оптим-ое сочетание факторов произ-ва. Изокванты могут иметь разную конфигурацию, что связано со способ-тью произ-ных факторов замещать др друга в процессе произ-ва. Если факторы произ-ва выступают относит-но др др абсол-ными субститутами, то изокванта линейна, а MRTS предст соб неизменную величину, т.е. наклон изокванты неизменен. (рис 3) Если факторы произ-ва выступают абсол-но комплементарными относ-но др др, то изокванта принимает принцип-но иной вид (рис 4). Замещение одного фактора произ-ва другим нецелесообразно: труд и капитал комбинир-ся в единст-но возм-ом сочетании факторов произ-ва дл кажд дан-го объема произ-ва (А,В,С). , явл-ся обощением произ-ных ф-ций трех первых типов: если β стремится к -1, ф-ция стремится к линейн произ ф-ции; если βприближ-ся к 0, то ф-ция – ф-ция К-Д; если β стремится к ∞, то ф-ция стрем-ся принять вид произ-ной ф-ции затраты-выпуск.
, явл-ся обощением произ-ных ф-ций трех первых типов: если β стремится к -1, ф-ция стремится к линейн произ ф-ции; если βприближ-ся к 0, то ф-ция – ф-ция К-Д; если β стремится к ∞, то ф-ция стрем-ся принять вид произ-ной ф-ции затраты-выпуск. не равна 0, то она должна присутсвовать и в остатках регрессии
не равна 0, то она должна присутсвовать и в остатках регрессии  , получающихся в результате обычного МНК. В тесте Дарбина-Уотсона для оценки автокорреляции используется статистика
, получающихся в результате обычного МНК. В тесте Дарбина-Уотсона для оценки автокорреляции используется статистика  Корректное использование статистики возможно при выполнении следующих условий:
Корректное использование статистики возможно при выполнении следующих условий: , где
, где  - оценка коэффициента авторегрессии; n-число наблюдений;
- оценка коэффициента авторегрессии; n-число наблюдений;  - выборочная дисперсия коэффициента при лаговой переменной
- выборочная дисперсия коэффициента при лаговой переменной  уравнения регрессии
уравнения регрессии  . При большом объеме выборки и справедливости нулевой гипотезы
. При большом объеме выборки и справедливости нулевой гипотезы  статистика h имеет стандартизированное нормальное распределение (h
статистика h имеет стандартизированное нормальное распределение (h  N(0,1)). Это позволяет по заданному уровню значимости определить критическую точку и сравнить h-статистику с ней. Если h-статистика больше критической точки, то нулевая гипотеза отвергается. Значение
N(0,1)). Это позволяет по заданному уровню значимости определить критическую точку и сравнить h-статистику с ней. Если h-статистика больше критической точки, то нулевая гипотеза отвергается. Значение  . А
. А 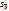 оценки
оценки 
 >1.
>1.


