Модель экономического роста Солоу.

Модель названа в честь экономиста Роберта Солоу и была разработана в 1950-1969 гг. В 1987 г. Р. Солоу получил Нобелевскую премию по экономике за работы по теории экономического роста. Модель Солоу позволяет оценивать разные варианты экономической политики государства, ее влияние на уровень жизни, прогнозировать, какая часть произведенного продукта должна потребляться сегодня, а какая его часть должна сберегаться для увеличения потребления в будущем. Поскольку сбережения равны инвестициям, то именно они определяют объём капитала, которым экономика будет располагать в будущем. В модели показаны, как рост запасов капитала, рабочей силы и улучшение технологии воздействуют на объём производства, а следовательно, на темпы экономического роста национального дохода во времени. В своей модели Р. Солоу исходит из классической предпосылки теории рыночного равновесия, что спрос на товары предъявляется со стороны: потребителей и инвесторов. Другими словами, продукция, произведенная каждым рабочим, делится между потреблением, приходящимся на одного рабочего, и инвестициями в расчете на одного рабочего: y = c + i. Модель Солоу предполагает, что функция потребления принимает простую форму: С = (1 – S) * Y, где s (норма сбережений) принимает значения от 0 до 1. Эта функция означает, что потребление пропорционально доходу. Каждый год часть дохода Y потребляется (1 – s) и часть сберегается (s). Роль такой трактовки потребления выяснится, если мы заменим в тождестве национальных счетов величину c (потребление) на (1 – s) * y, тогда оно будет иметь следующий вид: Y = (1-S) * Y + I. После преобразования получим: i = sy. Это уравнение показывает, что I (инвестиции), как и потребление, пропорциональны доходу. Если инвестиции равны сбережениям, то норма сбережений (s) показывает, какая часть произведенной продукции направляется на капитальные вложения. Представив модель Солоу как функцию производства и как функцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост страны. Общая величина капитала в национальной экономике может изменяться по двум причинам: 1) инвестиции приводят к росту объемов капитала; 2) часть капитала изнашивается, то есть амортизируется, что приводит к его уменьшению. Для того, чтобы понять, как изменяется объем капитала, необходимо выявить факторы, определяющие величину инвестиций и амортизации. Инвестиции (i) в расчете на одного работника, занятого в отраслях национальной экономики, являются частью валового внутреннего продукта, приходящегося на одного работника (sу). Заменив (y) выражением производственной функции y = f(k), представим инвестиции на одного работника как функцию от капиталовооруженности национальной экономики: i = sf (k). Из данного уравнения следует, что чем выше уровень капиталовооруженности k, тем выше объём производства f(k) и больше инвестиций i. На рис.1 показано, как норма сбережений определяет разделение продукта на потребление и инвестиции для каждого из значений k. Чтобы учесть в прогнозной модели фактор амортизации, предположим, что ежегодно выбывает определенная доля капитала (q – норма выбытия). Таким образом, количество капитала, которое выбывает каждый год, составляет qk. Ежегодно выбывает определенная фиксированная часть капитала, поэтому выбытие пропорционально запасам капитала.

Рис. 1. Производство, потребление, инвестиции.

Влияние инвестиций и выбытия на запасы капитала можно выразить с помощью следующего уравнения: «изменение запасов капитала = инвестиции – выбытие» - Dk = i – qk, где Dk есть изменение запасов капитала, приходящихся на одного работника за год. Поскольку инвестиции равны сбережениям, изменение запасов капитала может быть записано так: Dk = sf(k) – qk. На рисунке 2 инвестиции и выбытие показаны для различных уровней капиталовооруженности k.

 

 

Рис. 2. Взаимосвязь инв-ий, амортизации и уровня капиталовооруженности в нац-ой экономике.

Чем выше капиталовооруженность, тем больше объём производства и инвестиций, приходящихся на одного работника. Однако, чем больше объем капитала, тем больше и величина выбытия. На этом рис. 3.2 показано, что существует единственный уровень капиталовооруженности, при котором инвестиции равны величине износа. Если в экономике достигнут именно такой уровень, то он не будет меняться во времени, поскольку две действующие на него силы (инвестиции и выбытие) точно сбалансированы. Таким образом, при данном уровне капиталовооруженности Dk = 0. Назовем эту ситуацию состоянием устойчивой капиталовооруженности и обозначим его k*. Устойчивый уровень капиталовооруженности соответствует равновесию экономики в долгосрочном плане. Независимо от первоначального объема капитала, с которым экономика начинает развиваться, она затем достигает устойчивого состояния. Предположим, что запасы капитала ниже устойчивого уровня, как это имеет место в точке k1 на рис. 3.2. В этом случае инвестиции превышают выбытие. Таким образом, капиталовооруженность увеличивается и будет расти вместе с производством до тех пор, пока не приблизится к устойчивому уровню k*. Аналогично предположим, что запасы капитала в начальном состоянии превышают k*, например, в точке k2. В этом случае инвестиции меньше, чем выбытие – капитал выбывает быстрее, чем добавляется. Таким образом, капиталовооруженность будет сокращаться, опять приближаясь к устойчивому уровню.

все ограничения в виде неравенств содержат вогнутые функции , а ограничения в виде равенств содержат линейные функции . Тогда если существует решение , удовлет­воряющее условиям Куна—Таккера (3) — (7), то х* — оп­тимальное решение задачи нелинейного программирования. Если условия теоремы 2 выполняются, то нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования.
13. Задача нелинейного программирования и методы их решения. Теорема Куна-Таккера.

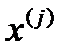В задаче нелинейного программирования (НЛП) требуется найти значение многомерной переменной х=(), минимизирующее целевую функцию f(x) при условиях, когда на переменную х наложены ограничения типа неравенств , i=1,2, (1), а переменные , т.е. компоненты вектора х, неотрицательны: 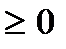(2). Рассмотрим общую задачу оптимизации, содержащую несколь­ко ограничений в виде равенств: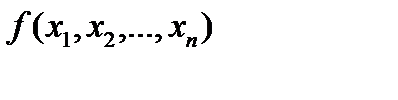 , при ограничениях: 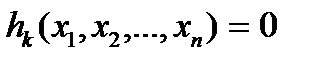, k=1,..,n. Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции k независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи с n до n-k. Метод исключения переменных применим лишь в тех случаях, когда уравнения, представляющие ограничения, можно разрешить относительно некоторого конкретного набора независимых пере­менных. При наличии большого числа ограничений в виде равенств, процесс исключения переменных становится весьма трудоемкой процедурой. С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде ра­венств. При этом задача с ограничениями преобразуется в эквива­лентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Ла­гранжа. Рассмотрим задачу минимизации функции n переменных с уче­том одного ограничения в виде равенства: (3), при ограничениях: (4). В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации: L(x,u)=f(x)-u*h(x) (5). Функция L(х;u) называется функцией Лагранжа, u — неизвест­ная постоянная, которая носит название множителя Лагранжа. Множители Лаг­ранжа можно использовать при построении критериев оптималь­ности для задач оптимизации с ограничениями в виде равенств. Кун и Таккер обобщили этот подход на случай общей задачи нели­нейного программирования с ограничениями, как в виде равенств, так и в виде неравенств.Рассмотрим следующую общую задачу не­линейного программирования: (0), при ограничениях: (1) (2). Определение: Ограничение в виде неравенства называется активным, или связывающим, в точке , если , и неактивным, или несвязывающим, если . Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования, исходя из предположения о дифференцируемости функций . Эти условия оптимальности, широко известные как условия Куна—Таккера, можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна—Таккера. 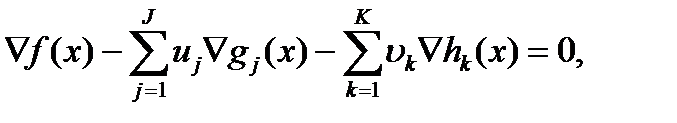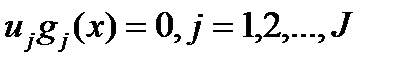Найти векторы , удовлетворяющие следующим условиям (3) (4) (5) (6) (7). Для того чтобы интерпретировать условия Куна — Таккера, рассмотрим задачу нелинейного программирования с ограничения­ми в виде равенств: , при ограничениях: Запишем условия Куна—Таккера: (8) (9). 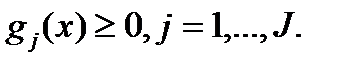Далее рассмотрим функцию Лагранжа для задачи нелинейного программирования с ограничениями в виде равенств: Для этой функции условия оптимальности первого порядка запи­сываются в виде: Рассмотрим задачу нелинейного программирования с ограни­чениями в виде неравенств: , при ограничениях Запишем условия Куна—Таккера: Соответствующая функция Лагранжа имеет вид: 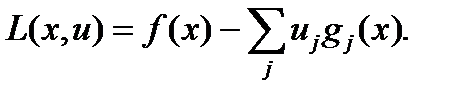Условия оптимальности первого порядка записываются как Теорема 1. Необходимость условий Куна—Таккера. Рассмотрим задачу нелинейного программирования (0)-(2). Пусть - дифференцируемые функции, а х* — допус­тимое решение данной задачи. Положим . Далее пусть линейно неза­висимы. Если х* — оптимальное решение задачи нелинейного про­граммирования, то существует такая пара векторов 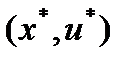, что является решением задачи Куна—Таккера (3)—(7). Условие, согласно которому должны быть линейно независимыми, известно как ус­ловие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое поч­ти всегда выполняется для встречающихся на практике задач опти­мизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свой­ствами. 1. Все ограничения в виде равенств и неравенств содержат линейные функции. 2. Все ограничения в виде неравенств содержат вогнутые функ­ции, все ограничения-равенства — линейные функции, а также существует, по крайней мере, одна допустимая точка х, которая рас­положена во внутренней части области, определяемой ограниче­ниями-неравенствами. Другими словами, существует такая точка х, что Если условие линейной независимости в точке оптимума не вы­полняется, то задача Куна—Таккера может не иметь решения. Теорема о необходимости условий Куна—Таккера позволяет идентифицировать неоптимальные точки. Другими словами, тео­рему 1 можно использовать для доказательства того, что задан­ная допустимая точка, удовлетворяющая условию линейной неза­висимости, не является оптимальной, если она не удовлетворяет условиям Куна—Таккера. С другой стороны, если в этой точке условия Куна—Таккера выполняются, то нет гарантии, что най­дено оптимальное решение нелинейной задачи. В качестве примера рассмотрим следующую задачу нелинейного программирования. Следующая теорема устанавливает условия, при выполнении которых точка Куна—Таккера автоматически соответствует оптимальному решению задачи нелинейного программирования. Теорема.2 Достаточность условий Куна—Таккера. Рассмотрим задачу нелинейного программирования (0) — (2). Пусть целевая функция выпуклая,