Неокл зад потреб-я заключ-ся в выборе набора тов и услуг при заданном отношении предпочтения (или ф-ции полезности) и «бюджетном огр-нии», кот относит потребителя к некот подмн-ву пространства товаров. Бюджетн огр-ние озн-ет, что денежные расходы на все тов и услуги не могут превышать денежного дохода. При этом вектор, состоящий из n цен в денежном выражении  где
где  - цена товара j и денежный дох I будут считаться заданными положит-ными параметрами. В таком случае бюджет огр-ние, отражающее то обстоятельство, что общ расх не может превышать дохода, будет иметь вид
- цена товара j и денежный дох I будут считаться заданными положит-ными параметрами. В таком случае бюджет огр-ние, отражающее то обстоятельство, что общ расх не может превышать дохода, будет иметь вид  где
где  - расход на тов j. Допустимым мн-вом для потребителя чвл-ся мн-во Х
- расход на тов j. Допустимым мн-вом для потребителя чвл-ся мн-во Х  т.е. непустое компактное (замкнутое и ограниченное) выпуклое подмн-во пространства товаров. Граница, вдоль кот
т.е. непустое компактное (замкнутое и ограниченное) выпуклое подмн-во пространства товаров. Граница, вдоль кот  , называется бюджетн линией. В случае n=2 это прямая, при n=3 это – плоскость и в общ случае – гиперплоскость. Т.обр, неокл зад потреб-я заключ-ся в выборе такого набора
, называется бюджетн линией. В случае n=2 это прямая, при n=3 это – плоскость и в общ случае – гиперплоскость. Т.обр, неокл зад потреб-я заключ-ся в выборе такого набора  из допустимого мн-ва Х, кот явл-ся самым предпочтительным, т.е. для всех остальных наборов x, принадлежащих Х, справедливо соотношение
из допустимого мн-ва Х, кот явл-ся самым предпочтительным, т.е. для всех остальных наборов x, принадлежащих Х, справедливо соотношение  . В терминах функции полезности задача формир-ся след обр:
. В терминах функции полезности задача формир-ся след обр:  или в развернутой форме
или в развернутой форме  , при условии
, при условии  где
где  и I – заданные положит-ые параметры. Здесь мы имеем задачу нелинейного программирования, в кот инструментальными переменными явл-ся уровни потребления каждого из n товаров
и I – заданные положит-ые параметры. Здесь мы имеем задачу нелинейного программирования, в кот инструментальными переменными явл-ся уровни потребления каждого из n товаров  ; в кач-ве целевой ф-ции выступает ф-ция полезности
; в кач-ве целевой ф-ции выступает ф-ция полезности  , кот считается непрерывно дифференцируемой и имеет положит-ые первые частные производные и отрицат-но определенную метрицу Гессе вторых частных производных; огран-ем в форме неравенства явл-ся бюджетное огр-ние, в кот ф-ция орган-ния линейна при заданных ценах
, кот считается непрерывно дифференцируемой и имеет положит-ые первые частные производные и отрицат-но определенную метрицу Гессе вторых частных производных; огран-ем в форме неравенства явл-ся бюджетное огр-ние, в кот ф-ция орган-ния линейна при заданных ценах  , а константой явл-ся дох I. В силу того, что целев ф-ция непрерывна, а допустим мн-во компактно, по тер Вейерштрасса решение этой зад сущ-ет, а т.к. целев ф-ция строго вогнуто и допус мн-во выпукло, то по «локально глобальной тереме» оно единственно. Неох и дост усл-ми для реш этой неокл зад потреб-ния явл-ся условия Куна-Таккера для (1). Определим ф-цию Лагранжа
, а константой явл-ся дох I. В силу того, что целев ф-ция непрерывна, а допустим мн-во компактно, по тер Вейерштрасса решение этой зад сущ-ет, а т.к. целев ф-ция строго вогнуто и допус мн-во выпукло, то по «локально глобальной тереме» оно единственно. Неох и дост усл-ми для реш этой неокл зад потреб-ния явл-ся условия Куна-Таккера для (1). Определим ф-цию Лагранжа  где λ – множитель Лагранжа, и запишем усл-вия Куна-Таккера
где λ – множитель Лагранжа, и запишем усл-вия Куна-Таккера 
 (3). Все переменные и частные производные здесь вычисляются в
(3). Все переменные и частные производные здесь вычисляются в 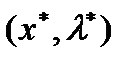 , где вектор
, где вектор  - решение задачи (1). Т. обр,
- решение задачи (1). Т. обр,  поэтому для всех закупленных предметов потребления справедливо соотношение (для
поэтому для всех закупленных предметов потребления справедливо соотношение (для  ).
).  для всех j, для кот
для всех j, для кот  (2). Это правило формулируется так: отношение предельной полезности к цене д.б. одинаковым для всех закупленных предметов потребления. Считая, что некот товары были куплены, из (2) получим, что оптим-ый множитель Лагранжа
(2). Это правило формулируется так: отношение предельной полезности к цене д.б. одинаковым для всех закупленных предметов потребления. Считая, что некот товары были куплены, из (2) получим, что оптим-ый множитель Лагранжа  д.б. положит-ым, а из этого следует по усл-ям Куна-Таккера, что весь доход д.б. израсходован
д.б. положит-ым, а из этого следует по усл-ям Куна-Таккера, что весь доход д.б. израсходован  , т.е. решение лежит на бюджетной прямой. Это сразу следует из факта ненасыщения: если использован не весь дох, то оставшуюся сумму денег можно было затратить на приобретение некот товара и тем самым увеличить полезность.
, т.е. решение лежит на бюджетной прямой. Это сразу следует из факта ненасыщения: если использован не весь дох, то оставшуюся сумму денег можно было затратить на приобретение некот товара и тем самым увеличить полезность.
Считается, потребители покупают все виды товаров и услуг (в противном случае можно уменьшить размерность пространства товаров, исключив из рассмотрения непокуп-мые товары). Тогда усл-ие (3) примет вид  или в развернутой форме
или в развернутой форме  Эти усл-я выполняются только в точке
Эти усл-я выполняются только в точке  , где
, где  явл-ся решением задачи потребления. Например, в случае двух товаров решение должно удовлетворять системе
явл-ся решением задачи потребления. Например, в случае двух товаров решение должно удовлетворять системе
 (4)Геометрически реш лежит в точке касания бюдж линии и кривой безразличия (рис 1). Наклон бюдж линии равен
(4)Геометрически реш лежит в точке касания бюдж линии и кривой безразличия (рис 1). Наклон бюдж линии равен  , а наклон крив безразличия
, а наклон крив безразличия 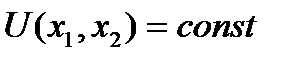 находится из выражения
находится из выражения 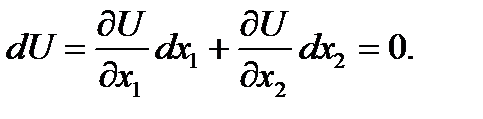 и составляет
и составляет  В точке касания наклоны равны
В точке касания наклоны равны  или
или  (5). Это условие можно получить из (4) исключив множитель Лагранжа. Оптим мн-ль Лагранжа, равный общему отношению предельной полезности к цене в (5), измеряется в полезности единицы тов j, деленной на кол-во долларов на единицу тов j, чо сводится к полезности на доллар. λ* следует интерпретировать как пред полезность добавочного дохода.
(5). Это условие можно получить из (4) исключив множитель Лагранжа. Оптим мн-ль Лагранжа, равный общему отношению предельной полезности к цене в (5), измеряется в полезности единицы тов j, деленной на кол-во долларов на единицу тов j, чо сводится к полезности на доллар. λ* следует интерпретировать как пред полезность добавочного дохода.
18. Временные ряды. Их основные характеристики и процедуры сглаживания.
Временным рядом назыв числовая последовательность, характеризующая изменение экономич явления во времени. Отдельное наблюдение этого ряда назыв уровнем временного ряда. В завис-ти от характера изучаемых показателей врем ряды делятся на интервальные, моментные и производные. Интервальными времен рядами назыв-ся такие ряды, в кот кажд уровень характеризует величину изучаемого явления за соответствующий интервал времени, например, выработку за день, месяц, год. В моментных врем рядах уровень отражает величину изучаемого явления на опред-ный момент времени, напр, числен-ть рабочих предприятия на 1 янв 2003г. Уровни, характеризующие интервалы или моменты времени с пом средних или относит-х величин образуют производные времен ряды. Врем ряд должен правильно отражать объективный процесс развития экон-го объекта. Для этого необх-мо, чтобы уровни врем ряда состояли из однородных сопоставимых величин. Эта сопоставимость достигается в рез-те одинакового подхода к наблюдениям ряда на разных этапах его формирования. Кроме того, уровни врем рядов должны выражаться в одних и тех же единицах измерения и должны рассчитываться по одной и той же методологии. Прежде чем, данные врем ряда  будут использованы для построения эконометрической модели, они подвергаются анализу. Обычно этот анализ сводится к тому, что выясняется, как врем ряд отражает изменения, происходящие в изучаемом явлении. Для этого вычисляют первые разности (абсолютные приросты), характеризующие скорость развития этого явления
будут использованы для построения эконометрической модели, они подвергаются анализу. Обычно этот анализ сводится к тому, что выясняется, как врем ряд отражает изменения, происходящие в изучаемом явлении. Для этого вычисляют первые разности (абсолютные приросты), характеризующие скорость развития этого явления  , где
, где 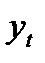 - уровень врем ряда в момент
- уровень врем ряда в момент  . Абсолютный прирост – мгновенная характер-ка, кот не дает представления о поведении изучаемого процесса в целом. Чтобы получить такое представление обычно вычисляют средний абсол-й прирост
. Абсолютный прирост – мгновенная характер-ка, кот не дает представления о поведении изучаемого процесса в целом. Чтобы получить такое представление обычно вычисляют средний абсол-й прирост  (1). Кроме абсолютной, принято вычислять относительную скорость изменения изучаемого явления. Показателями относ-ной скорости явл-ются темп роста и темп прироста, кот вычисл-ся по формулам
(1). Кроме абсолютной, принято вычислять относительную скорость изменения изучаемого явления. Показателями относ-ной скорости явл-ются темп роста и темп прироста, кот вычисл-ся по формулам 
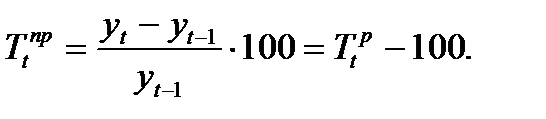 Для опред-ния средней относит скорости изменения за весь рассматриваемый период вычисл-ют сред темп роста по средней геометрической
Для опред-ния средней относит скорости изменения за весь рассматриваемый период вычисл-ют сред темп роста по средней геометрической  (2), где
(2), где  - темпы роста за отдел интервалы времени. Как показывают формулы (1) и (2), средние характеристики не всегда дают правильное представление о характере поведения изучаемого явления, т.к. их величины зависят только от крайних членов, кот м.б. сильно искажены воздействием случайной компоненты. Поэтому возникает необх-ть снижение влияния случ-ой составляющей на уровни времен ряда. Методы, позволяющие снизить это влияние, принято называть процедурами сглаживания. Процедуры сглаживания строят т.обр, чтобы они обеспечивали минимизацию случайных отклонений уровней врем ряда от некоторой гладкой кривой предполагаемого тренда (закономерности) изучаемого процесса. Наиболее простой и распространенный прием заключается в расчете скользящих средних. Суть этого приема в следующем. Для каждых m-последовательных уровней врем ряда (m < n)подсчитывается сред величина. Причем, вычислив знач-е средней для первых m-уровней
- темпы роста за отдел интервалы времени. Как показывают формулы (1) и (2), средние характеристики не всегда дают правильное представление о характере поведения изучаемого явления, т.к. их величины зависят только от крайних членов, кот м.б. сильно искажены воздействием случайной компоненты. Поэтому возникает необх-ть снижение влияния случ-ой составляющей на уровни времен ряда. Методы, позволяющие снизить это влияние, принято называть процедурами сглаживания. Процедуры сглаживания строят т.обр, чтобы они обеспечивали минимизацию случайных отклонений уровней врем ряда от некоторой гладкой кривой предполагаемого тренда (закономерности) изучаемого процесса. Наиболее простой и распространенный прием заключается в расчете скользящих средних. Суть этого приема в следующем. Для каждых m-последовательных уровней врем ряда (m < n)подсчитывается сред величина. Причем, вычислив знач-е средней для первых m-уровней  переходят к расчету средней для уровней
переходят к расчету средней для уровней  и т.д. Т.обр, интервал, для кот подсчитывается средняя как бы скользит по врем ряду с шагом, равным единице. Если
и т.д. Т.обр, интервал, для кот подсчитывается средняя как бы скользит по врем ряду с шагом, равным единице. Если  нечетной, а предпочтительнее брать для сглаживания нечетной число уровней, поскольку тогда рассчитанное (сглаженное) зн-е окажется в центре интервала сглаживания и может легко заменить фактич зн-е, то для опред-ния скользящей средней можно записать след формулу
нечетной, а предпочтительнее брать для сглаживания нечетной число уровней, поскольку тогда рассчитанное (сглаженное) зн-е окажется в центре интервала сглаживания и может легко заменить фактич зн-е, то для опред-ния скользящей средней можно записать след формулу 
 - зн-е скользящей средней для момента
- зн-е скользящей средней для момента  ,
,  - фактич зн-е уровня в момент i. Расчте скользящей средней при большом числе уровней можно несколько упростить, используя рекурсивную формулу
- фактич зн-е уровня в момент i. Расчте скользящей средней при большом числе уровней можно несколько упростить, используя рекурсивную формулу  Сглаживание с пом скользящей средней явл-ся частным случаем взвешенной скользящей средней, весовые коэф-ты кот опред-ются по МНК, путем минимизации выражения
Сглаживание с пом скользящей средней явл-ся частным случаем взвешенной скользящей средней, весовые коэф-ты кот опред-ются по МНК, путем минимизации выражения  (3), если в кач-ве полинома используется парабола. Для
(3), если в кач-ве полинома используется парабола. Для 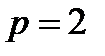 с пом (3) получаем весовые коэф-ты, позволяющие взвешенную скользящую среднюю можно записать в след виде
с пом (3) получаем весовые коэф-ты, позволяющие взвешенную скользящую среднюю можно записать в след виде  Для случая, когда в расчете взвешенной скользящей средней используется 7 точек (p=3) сглаживания осущ-ся по формуле
Для случая, когда в расчете взвешенной скользящей средней используется 7 точек (p=3) сглаживания осущ-ся по формуле  Сглаженные данные предпочтительней испол-ть для анализа динамики, т.к. процедура сглаживания сводит к минимуму влияние случ составляющей. Следоват-но, такие характер-ки, как средний абсол прирост или темп роста, будут свободны от искажения случ компонентой. Однако, сглаживание приводит к сокращению числа уровней врем ряда, что весьма нежелательно в тех случаях, когда врем ряд короткий.
Сглаженные данные предпочтительней испол-ть для анализа динамики, т.к. процедура сглаживания сводит к минимуму влияние случ составляющей. Следоват-но, такие характер-ки, как средний абсол прирост или темп роста, будут свободны от искажения случ компонентой. Однако, сглаживание приводит к сокращению числа уровней врем ряда, что весьма нежелательно в тех случаях, когда врем ряд короткий.


 где
где  - цена товара j и денежный дох I будут считаться заданными положит-ными параметрами. В таком случае бюджет огр-ние, отражающее то обстоятельство, что общ расх не может превышать дохода, будет иметь вид
- цена товара j и денежный дох I будут считаться заданными положит-ными параметрами. В таком случае бюджет огр-ние, отражающее то обстоятельство, что общ расх не может превышать дохода, будет иметь вид  где
где  - расход на тов j. Допустимым мн-вом для потребителя чвл-ся мн-во Х
- расход на тов j. Допустимым мн-вом для потребителя чвл-ся мн-во Х  т.е. непустое компактное (замкнутое и ограниченное) выпуклое подмн-во пространства товаров. Граница, вдоль кот
т.е. непустое компактное (замкнутое и ограниченное) выпуклое подмн-во пространства товаров. Граница, вдоль кот  , называется бюджетн линией. В случае n=2 это прямая, при n=3 это – плоскость и в общ случае – гиперплоскость. Т.обр, неокл зад потреб-я заключ-ся в выборе такого набора
, называется бюджетн линией. В случае n=2 это прямая, при n=3 это – плоскость и в общ случае – гиперплоскость. Т.обр, неокл зад потреб-я заключ-ся в выборе такого набора  из допустимого мн-ва Х, кот явл-ся самым предпочтительным, т.е. для всех остальных наборов x, принадлежащих Х, справедливо соотношение
из допустимого мн-ва Х, кот явл-ся самым предпочтительным, т.е. для всех остальных наборов x, принадлежащих Х, справедливо соотношение  . В терминах функции полезности задача формир-ся след обр:
. В терминах функции полезности задача формир-ся след обр:  или в развернутой форме
или в развернутой форме  , при условии
, при условии  где
где  и I – заданные положит-ые параметры. Здесь мы имеем задачу нелинейного программирования, в кот инструментальными переменными явл-ся уровни потребления каждого из n товаров
и I – заданные положит-ые параметры. Здесь мы имеем задачу нелинейного программирования, в кот инструментальными переменными явл-ся уровни потребления каждого из n товаров  ; в кач-ве целевой ф-ции выступает ф-ция полезности
; в кач-ве целевой ф-ции выступает ф-ция полезности  , кот считается непрерывно дифференцируемой и имеет положит-ые первые частные производные и отрицат-но определенную метрицу Гессе вторых частных производных; огран-ем в форме неравенства явл-ся бюджетное огр-ние, в кот ф-ция орган-ния линейна при заданных ценах
, кот считается непрерывно дифференцируемой и имеет положит-ые первые частные производные и отрицат-но определенную метрицу Гессе вторых частных производных; огран-ем в форме неравенства явл-ся бюджетное огр-ние, в кот ф-ция орган-ния линейна при заданных ценах  где λ – множитель Лагранжа, и запишем усл-вия Куна-Таккера
где λ – множитель Лагранжа, и запишем усл-вия Куна-Таккера 
 (3). Все переменные и частные производные здесь вычисляются в
(3). Все переменные и частные производные здесь вычисляются в 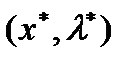 , где вектор
, где вектор  - решение задачи (1). Т. обр,
- решение задачи (1). Т. обр,  поэтому для всех закупленных предметов потребления справедливо соотношение (для
поэтому для всех закупленных предметов потребления справедливо соотношение (для  ).
).  для всех j, для кот
для всех j, для кот  (2). Это правило формулируется так: отношение предельной полезности к цене д.б. одинаковым для всех закупленных предметов потребления. Считая, что некот товары были куплены, из (2) получим, что оптим-ый множитель Лагранжа
(2). Это правило формулируется так: отношение предельной полезности к цене д.б. одинаковым для всех закупленных предметов потребления. Считая, что некот товары были куплены, из (2) получим, что оптим-ый множитель Лагранжа  д.б. положит-ым, а из этого следует по усл-ям Куна-Таккера, что весь доход д.б. израсходован
д.б. положит-ым, а из этого следует по усл-ям Куна-Таккера, что весь доход д.б. израсходован  , т.е. решение лежит на бюджетной прямой. Это сразу следует из факта ненасыщения: если использован не весь дох, то оставшуюся сумму денег можно было затратить на приобретение некот товара и тем самым увеличить полезность.
, т.е. решение лежит на бюджетной прямой. Это сразу следует из факта ненасыщения: если использован не весь дох, то оставшуюся сумму денег можно было затратить на приобретение некот товара и тем самым увеличить полезность. или в развернутой форме
или в развернутой форме  Эти усл-я выполняются только в точке
Эти усл-я выполняются только в точке  , где
, где  явл-ся решением задачи потребления. Например, в случае двух товаров решение должно удовлетворять системе
явл-ся решением задачи потребления. Например, в случае двух товаров решение должно удовлетворять системе (4)Геометрически реш лежит в точке касания бюдж линии и кривой безразличия (рис 1). Наклон бюдж линии равен
(4)Геометрически реш лежит в точке касания бюдж линии и кривой безразличия (рис 1). Наклон бюдж линии равен  , а наклон крив безразличия
, а наклон крив безразличия 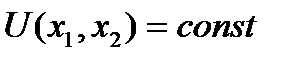 находится из выражения
находится из выражения 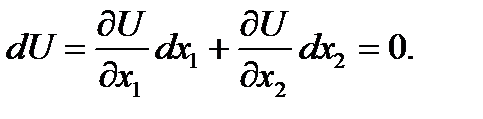 и составляет
и составляет  В точке касания наклоны равны
В точке касания наклоны равны  или
или  (5). Это условие можно получить из (4) исключив множитель Лагранжа. Оптим мн-ль Лагранжа, равный общему отношению предельной полезности к цене в (5), измеряется в полезности единицы тов j, деленной на кол-во долларов на единицу тов j, чо сводится к полезности на доллар. λ* следует интерпретировать как пред полезность добавочного дохода.
(5). Это условие можно получить из (4) исключив множитель Лагранжа. Оптим мн-ль Лагранжа, равный общему отношению предельной полезности к цене в (5), измеряется в полезности единицы тов j, деленной на кол-во долларов на единицу тов j, чо сводится к полезности на доллар. λ* следует интерпретировать как пред полезность добавочного дохода. будут использованы для построения эконометрической модели, они подвергаются анализу. Обычно этот анализ сводится к тому, что выясняется, как врем ряд отражает изменения, происходящие в изучаемом явлении. Для этого вычисляют первые разности (абсолютные приросты), характеризующие скорость развития этого явления
будут использованы для построения эконометрической модели, они подвергаются анализу. Обычно этот анализ сводится к тому, что выясняется, как врем ряд отражает изменения, происходящие в изучаемом явлении. Для этого вычисляют первые разности (абсолютные приросты), характеризующие скорость развития этого явления  , где
, где 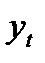 - уровень врем ряда в момент
- уровень врем ряда в момент  . Абсолютный прирост – мгновенная характер-ка, кот не дает представления о поведении изучаемого процесса в целом. Чтобы получить такое представление обычно вычисляют средний абсол-й прирост
. Абсолютный прирост – мгновенная характер-ка, кот не дает представления о поведении изучаемого процесса в целом. Чтобы получить такое представление обычно вычисляют средний абсол-й прирост  (1). Кроме абсолютной, принято вычислять относительную скорость изменения изучаемого явления. Показателями относ-ной скорости явл-ются темп роста и темп прироста, кот вычисл-ся по формулам
(1). Кроме абсолютной, принято вычислять относительную скорость изменения изучаемого явления. Показателями относ-ной скорости явл-ются темп роста и темп прироста, кот вычисл-ся по формулам 
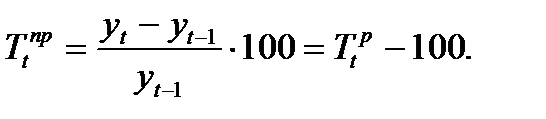 Для опред-ния средней относит скорости изменения за весь рассматриваемый период вычисл-ют сред темп роста по средней геометрической
Для опред-ния средней относит скорости изменения за весь рассматриваемый период вычисл-ют сред темп роста по средней геометрической  (2), где
(2), где  - темпы роста за отдел интервалы времени. Как показывают формулы (1) и (2), средние характеристики не всегда дают правильное представление о характере поведения изучаемого явления, т.к. их величины зависят только от крайних членов, кот м.б. сильно искажены воздействием случайной компоненты. Поэтому возникает необх-ть снижение влияния случ-ой составляющей на уровни времен ряда. Методы, позволяющие снизить это влияние, принято называть процедурами сглаживания. Процедуры сглаживания строят т.обр, чтобы они обеспечивали минимизацию случайных отклонений уровней врем ряда от некоторой гладкой кривой предполагаемого тренда (закономерности) изучаемого процесса. Наиболее простой и распространенный прием заключается в расчете скользящих средних. Суть этого приема в следующем. Для каждых m-последовательных уровней врем ряда (m < n)подсчитывается сред величина. Причем, вычислив знач-е средней для первых m-уровней
- темпы роста за отдел интервалы времени. Как показывают формулы (1) и (2), средние характеристики не всегда дают правильное представление о характере поведения изучаемого явления, т.к. их величины зависят только от крайних членов, кот м.б. сильно искажены воздействием случайной компоненты. Поэтому возникает необх-ть снижение влияния случ-ой составляющей на уровни времен ряда. Методы, позволяющие снизить это влияние, принято называть процедурами сглаживания. Процедуры сглаживания строят т.обр, чтобы они обеспечивали минимизацию случайных отклонений уровней врем ряда от некоторой гладкой кривой предполагаемого тренда (закономерности) изучаемого процесса. Наиболее простой и распространенный прием заключается в расчете скользящих средних. Суть этого приема в следующем. Для каждых m-последовательных уровней врем ряда (m < n)подсчитывается сред величина. Причем, вычислив знач-е средней для первых m-уровней  переходят к расчету средней для уровней
переходят к расчету средней для уровней  и т.д. Т.обр, интервал, для кот подсчитывается средняя как бы скользит по врем ряду с шагом, равным единице. Если
и т.д. Т.обр, интервал, для кот подсчитывается средняя как бы скользит по врем ряду с шагом, равным единице. Если  нечетной, а предпочтительнее брать для сглаживания нечетной число уровней, поскольку тогда рассчитанное (сглаженное) зн-е окажется в центре интервала сглаживания и может легко заменить фактич зн-е, то для опред-ния скользящей средней можно записать след формулу
нечетной, а предпочтительнее брать для сглаживания нечетной число уровней, поскольку тогда рассчитанное (сглаженное) зн-е окажется в центре интервала сглаживания и может легко заменить фактич зн-е, то для опред-ния скользящей средней можно записать след формулу 
 - зн-е скользящей средней для момента
- зн-е скользящей средней для момента  ,
,  - фактич зн-е уровня в момент i. Расчте скользящей средней при большом числе уровней можно несколько упростить, используя рекурсивную формулу
- фактич зн-е уровня в момент i. Расчте скользящей средней при большом числе уровней можно несколько упростить, используя рекурсивную формулу  Сглаживание с пом скользящей средней явл-ся частным случаем взвешенной скользящей средней, весовые коэф-ты кот опред-ются по МНК, путем минимизации выражения
Сглаживание с пом скользящей средней явл-ся частным случаем взвешенной скользящей средней, весовые коэф-ты кот опред-ются по МНК, путем минимизации выражения  (3), если в кач-ве полинома используется парабола. Для
(3), если в кач-ве полинома используется парабола. Для 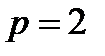 с пом (3) получаем весовые коэф-ты, позволяющие взвешенную скользящую среднюю можно записать в след виде
с пом (3) получаем весовые коэф-ты, позволяющие взвешенную скользящую среднюю можно записать в след виде  Для случая, когда в расчете взвешенной скользящей средней используется 7 точек (p=3) сглаживания осущ-ся по формуле
Для случая, когда в расчете взвешенной скользящей средней используется 7 точек (p=3) сглаживания осущ-ся по формуле  Сглаженные данные предпочтительней испол-ть для анализа динамики, т.к. процедура сглаживания сводит к минимуму влияние случ составляющей. Следоват-но, такие характер-ки, как средний абсол прирост или темп роста, будут свободны от искажения случ компонентой. Однако, сглаживание приводит к сокращению числа уровней врем ряда, что весьма нежелательно в тех случаях, когда врем ряд короткий.
Сглаженные данные предпочтительней испол-ть для анализа динамики, т.к. процедура сглаживания сводит к минимуму влияние случ составляющей. Следоват-но, такие характер-ки, как средний абсол прирост или темп роста, будут свободны от искажения случ компонентой. Однако, сглаживание приводит к сокращению числа уровней врем ряда, что весьма нежелательно в тех случаях, когда врем ряд короткий.


