Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность и точки разрыва.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 4. Найти точки разрыва и определить их тип Решение. Вычислить значение функции обычным путём здесь нельзя лишь в точках Во-первых, можно представить так: Надо найти оба односторонних предела в каждой из точек. Рассмотрим Для предела справа,
Для предела слева,
Получились разные константы. Значит, разрыв 1-го рода.
Рассмотрим Здесь
Хотя бы с одной стороны предел Ответ.
Чертёж к этой задаче. Синим цветом показан график этой функции, жёлтым - вертикальная асимптота, где разрыв 2-го рода. Задача 5. Исследовать тип точки разрыва Решение. И при Тогда для обоих односторонних пределов получается одинаково:
К тому же функция чётная, и так ясно, что с двух сторон симметричные ветви графика. Так что достаточно было вычислить только с одной стороны. Ответ. График этой функции:
Задача 6. Найти точки разрыва и установить их тип для функции Решение. Знаменталь дроби 0 при
Пределы конечные, но разные. Разрыв 1-го рода.
Пределы конечные, но разные. Разрыв 1-го рода. Ответ. График этой функции:
Задача 7. Исследовать тип точки Решение. Ищем односторонние пределы вокруг 0, но при этом каждый раз домножаем и делим на
Здесь знак модуля раскрывается по-разному в зависимости от того, справа или слева от 0 мы находимся. Это либо Ответ. Примечание. Вот график этой функции:
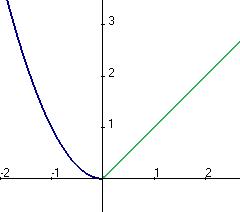
Задача 8. Выяснить тип точки Решение. Левосторонний предел здесь должен вычисляться с помощью первой ветви функции, а правосторонний с помощью второй. Значение функции существует и равно как левостороннему пределу, так и правостороннему. 0 это точка непрерывности. Ответ. График этой функции:
Задача 9. Найти точки разрыва и определить их тип для функции: Решение. Сначала ищем точки, подозрительные на разрыв, то есть где возможен разрыв. Во-первых, это точка стыковки двух ветвей графика, то есть Рассмотрим
Тогда Рассмотрим
Рассмотрим
На графике синим цветом показана левая ветвь функции, зелёным - правая, жёлтым - асимптота (она там, где разрыв 2 рода). Ответ.
Задача 10 (А,Б). Установить тип точки разрыва А) Решение. А вот при умножении на
Ответ. А) разрыв 2-го рода. Б) устранимый разрыв. Графики этих функций
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.008 с.) |

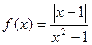 .
. где знаменатель обращается в 0. Эти две точки подозрительные на существование разрыва, мы и будем исследовать.
где знаменатель обращается в 0. Эти две точки подозрительные на существование разрыва, мы и будем исследовать.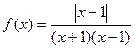 .
.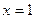 .
. и модуль раскрывается без лишнего знака:
и модуль раскрывается без лишнего знака: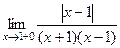 =
=  =
= 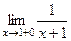 =
=  .
.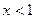 , и при раскрытии модуля знак минус:
, и при раскрытии модуля знак минус: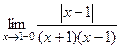 =
=  =
= 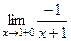 =
= 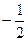 .
.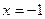 .
.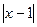 и
и 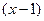 раскрываются одинаково, и равны 2 и
раскрываются одинаково, и равны 2 и  . А отличие в том, какого знака бесконечно-малая
. А отличие в том, какого знака бесконечно-малая 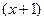 в знаменателе.
в знаменателе. =
=  =
=  =
= 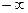 .
. =
=  =
=  =
=  .
.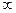 или не существует, значит разрыв 2-го рода.
или не существует, значит разрыв 2-го рода.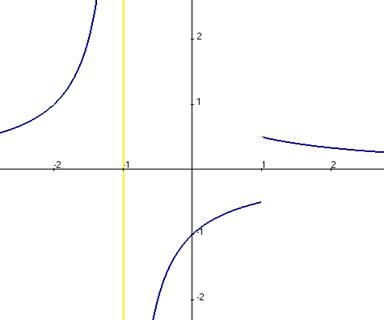
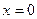 для
для 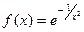 .
.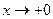 , и при
, и при  здесь
здесь 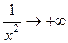 , а тогда
, а тогда 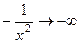 .
.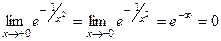 . Тогда разрыв устранимый.
. Тогда разрыв устранимый.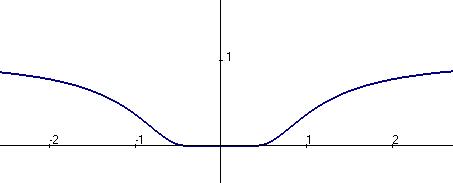
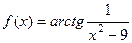 .
. и
и 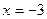 . Вычислим односторонние пределы в точках
. Вычислим односторонние пределы в точках  и 3. При этом учитываем, что
и 3. При этом учитываем, что 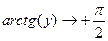 при
при 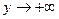 и
и  при
при 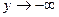 .
.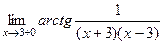 =
= 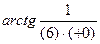 =
= 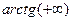 =
= 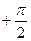 .
.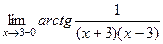 =
= 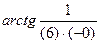 =
= 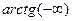 =
= 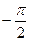 .
.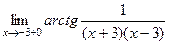 =
= 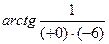 =
= 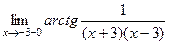 =
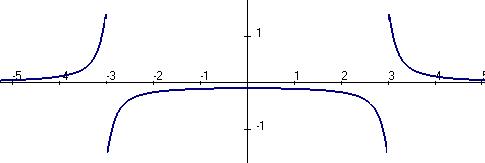
= 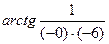 =
= 
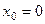 для функции
для функции 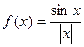 .
.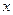 , так чтобы избавиться от синуса в выражении.
, так чтобы избавиться от синуса в выражении. =
= 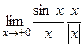 =
= 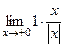 =
= 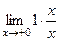 = 1.
= 1. =
= 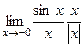 =
= 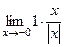 =
=  =
= 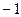 .
.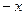 . Получились различные числа. Разрыв 1-го рода.
. Получились различные числа. Разрыв 1-го рода.
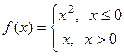 .
.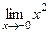 = 0.
= 0. 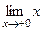 = 0. Кроме того,
= 0. Кроме того,  .
.
 .
.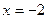 и
и 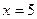 . Точка
. Точка 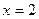 не должна рассматриваться, т.к. правее 1 уже действует другая ветвь функции.
не должна рассматриваться, т.к. правее 1 уже действует другая ветвь функции. ,
, 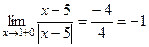 . Кроме того, значение в точке 1 тоже существует и равно
. Кроме того, значение в точке 1 тоже существует и равно 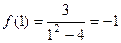 .
.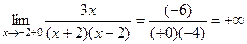 .
. 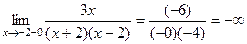 .
.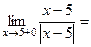
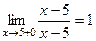 ,
, 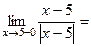
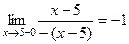 .
.
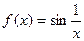 . Б)
. Б)  .
.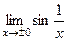 =
=  , такие пределы не существуют (бесконечное количество колебаний, ордината не устанавливается ни на каком уровне). Разрыв 2 рода.
, такие пределы не существуют (бесконечное количество колебаний, ордината не устанавливается ни на каком уровне). Разрыв 2 рода.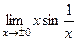 = 0 (произведение бесконечно-малой на ограниченную является бесконечно-малой).
= 0 (произведение бесконечно-малой на ограниченную является бесконечно-малой).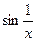 и
и  выглядят так:
выглядят так: и
и