
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 17 (18 ноября у обеих групп)Содержание книги
Поиск на нашем сайте
Задача 1. Найти предел Решение. В этом случае можно с помощью замены преобразовать так, что будут только целые степени, а для получившихся многочленов уже можно искать корни и проводить разложение на множители. НОК(2,3) = 6. Если обозначим
При этом, если * Такое совпадение при замене переменной бывает далеко не всегда, а лишь в частных случаях, а обычно надо пересчитать, возможно новая переменная стремится к другому числу. Например, если Итак,
При этом даже нет необходимости делать обратную замену и возвращаться к старой переменной. Ответ. Тема «1-й замечательный предел». Задача 2. Найти предел Решение. С помощью преобразований получим в знаменателе такое же выражение, как под знаком синуса в числителе.
Второй предел вообще не содержит неопределённости, а первый это в точности Ответ. Задача 3. Найти предел Решение. Ответ. 5.
Задача 4. Найти предел Решение.
Сначала домножили на сопряжённое выражение, потом вынесли в отдельный множитель ту часть, где нет неопределённости. В конце домножили на 6 в знаменателе и числителе, чтобы в знаменателе образовалось ровно такое же выражение, как под знаком синуса, то есть Ответ. 24. Задача 5. Найти предел Решение. Эту задачу можно решить как с применением тригонометрической формулы, так и методом Лопиталя. Способ 1. Вспомним формулу
Способ 2. Ответ. 2.
Задача 6. Найти предел Решение. Чтобы устранить разность, как всегда, домножим и поделим на сопряжённое.
это мы применили формулу понижения степени, а ту часть, которая стремится к 0, вычислили сразу, этот коэффициент теперь так и будет оставаться до ответа. Теперь заменим каждую из бесконечно-малых на эквивалентную.
Замечания. Начиная с того места, где мы получили Способ 2. По правилу Лопиталя. Способ 3. Домножить на сопряжённое.
Способ 3-а. Представить квадрат синуса в знаменателе в виде Задача 7. Найти предел
Решение.
Тогда Ответ. 1. Замечание. Почему выражение Задача 8. Найти предел Решение. Способ 1. С помощью замены на эквивалентную бесконечно-малую. Можно выделить 1 под знаком логарифма, получить выражение типа
Способ 2. По правилу Лопиталя Ответ. 6.
Задача 9. Найти предел Решение. Методом Лопиталя
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.008 с.) |

 .
. , то:
, то: ,
,  .
. , то и
, то и  тоже стремится к 1.
тоже стремится к 1. и
и  , то
, то 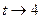 .
. =
=  (для удобства сделали, чтобы многочлены начинались со старшей степени). Далее,
(для удобства сделали, чтобы многочлены начинались со старшей степени). Далее, =
=  =
= 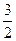 .
. .
. =
=  =
=  =
= 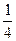 .
. если переобозначить
если переобозначить  .
. .
. =
=  = 5.
= 5.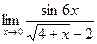 .
.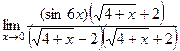 =
= =
=  =
= = 24.
= 24. .
. .
. . Получается
. Получается =
=  = 2.
= 2. =
=  =
=  = 2.
= 2. .
. =
=  =
= =
=  =
= =
= 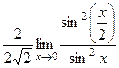 .
. =
=  =
=  =
= =
= 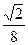 . Ответ.
. Ответ.  =
=  =
=  =
=  .
. =
=  =
= =
=  =
= 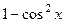 и тогда получается разбиение на 2 сопряжённых:
и тогда получается разбиение на 2 сопряжённых:  =
=  =
=  .
. =
=  =
= =
=  . Введём замену
. Введём замену 
 =
= 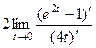 =
=  =
=  .
. мы здесь не домножаем на сопряжённое, а делали методом Лопиталя. Тогда получилось бы
мы здесь не домножаем на сопряжённое, а делали методом Лопиталя. Тогда получилось бы  =
=  , то есть в таких выражениях, в отличие от иррациональностей, формулу сокращённого умножения и структуру
, то есть в таких выражениях, в отличие от иррациональностей, формулу сокращённого умножения и структуру  применять бесполезно, потому что это даёт точно такое же выражение, стремящееся к
применять бесполезно, потому что это даёт точно такое же выражение, стремящееся к  .
. .
. . Затем воспользоваться эквивалентностью
. Затем воспользоваться эквивалентностью 
 =
=  =
=  =
=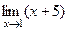 = 6.
= 6. =
=  = 6.
= 6. .
. =
=  =
=  . Но опять получилась неопределённость
. Но опять получилась неопределённость 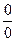 . Продифференцируем ещё раз
. Продифференцируем ещё раз  =
=  =
= =
=  =
=  = 0,32. Ответ.
= 0,32. Ответ. 


