
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос № 9 Дифракция на пространственной решетке. Формула Вульфа-Брегга.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную порядка 10-10 м и, Метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга советским физиком Г. В. Вульфом (1863—1925) и английскими физиками Г. и Л. Брэггами (отец (1862—1942) и сын (1890—1971)). Предположение Вульфа — Брэггов: дифракция рентгеновских лучей является результатом их отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки). Представим кристаллы в виде совокупности параллельных кристаллографических
плоскостей, отстоящих друг от друга на расстоянии d. Пучок параллельных монохроматических рентгеновских лучей (/, 2) падает под углом скольжения
т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн, наблюдается дифракционный максимум. При произвольном направлений падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоватьсянепрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Для таких условий опыта всегда найдутся длины волн, удовлетворяющие условию (14.10). Наблюдая дифракцию рентгеновских лучей известной длины волны на кристаллической структуре неизвестного строения и измеряя
Вопрос № 10 Дисперсия света. Области нормальной и аномальной дисперсии Итак, дисперсия света – это зависимость показателя преломления вещества от частоты световой волны
соответствуют нормальной дисперсии света (с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров. Дисперсия называется аномальной, если
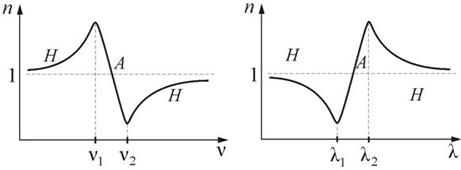
т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия. Зависимости n от ν и λ показаны на рис. 10.4 и 10.5.
В зависимости от характера дисперсии групповая скорость u в веществе может быть как больше, так и меньше фазовой скорости υ (в недиспергирующей среде Групповая скорость u связана с циклической частотой ω и волновым числом k соотношением:
Таким образом, при нормальной дисперсии u < υ и При аномальной дисперсии u > υ, и, в частности, если
Вопрос № 11 Естественный и поляризованный свет. Поляризация света при отражении. Закон Брюстера Испускание кванта света происходит в результате перехода электрона из возбужденного состояния в основное. Электромагнитная волна, испускаемая в результате этого перехода, является поперечной, то есть вектора Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают световые волна независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равновероятными колебаниями светового вектора Вектор Различает также эллиптически поляризованный свет: при распространении электрически поляризованного света вектор
Степенью поляризации называется величина
где Imax и Imin – максимальная и минимальная компоненты интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора Если вектор в эллиптически поляризованном свете вращается при распространении света по часовой стрелке, то поляризация называется правой, против - левой. В эллиптически поляризованном свете колебания полностью упорядочены. К эллиптически поляризованному свету понятие степени поляризации не применимо, так что Р=1 всегда. Наиболее просто поляризационный свет можно получить из естественного света при отражении световой волны от границы раздела двух диэлектриков. Если естественный свет падает на границу раздела двух диэлектриков (например, воздух-стекло), то часть его отражается, а часть преломляется и распространяется во второй среде.
Закон Брюстера: При угле падения, равном углу Брюстера іБ р: 1. отраженный от границы раздела двух диэлектриков луч будет полностью поляризован в плоскости, перпендикулярной плоскости падения; 2. степень поляризации преломленного луча достигает максимального значения меньшего единицы; 3. преломленный луч будет поляризован частично в плоскости падения; 4. угол между отраженным и преломленным лучами будет равен 90°; 4. тангенс угла Брюстера равен относительному показателю преломления
- закон Брюстера.
Степень поляризации преломленного света может быть значительно повышена многократным преломлением при условии падения света на границу раздела под углом Брюстера. Если для стекла (n = 1,53) степень поляризации преломленного луча составляет ≈15 %, то после преломления на 8-10 наложенных друг на друга стеклянных пластинках, вышедший свет будет практически полностью поляризован - стопа Столетова. Поляризованный свет можно получить из естественного с помощью поляризаторов - анизотропных кристаллов, пропускающих свет только в одном направлении (исландский шпат, кварц, турмалин). Вопрос № 12 Двойное лучепреломление. Поляризационные призмы и поляроиды. Закон Малюса. Все кристаллы, кроме кристаллов кубической система — изотропных кристаллов, являются анизотропными, то есть свойства кристаллов зависят от направления. Явление двойного лучепреломления впервые было обнаружено Барталином в 1667 г. на кристалле исландского шпата (разновидность СаСО3). Явление двойного лучепреломления заключается в следующем: луч света, падающий на анизотропный кристалл, разделяется в нем на два луча: обыкновенный и необыкновенный, распространяющиеся с разными скоростями Анизотропные кристаллы подразделяются на одноосные и двуосные.
Отличия между обыкновенными и необыкновенными лучами:
Различие скоростей U о и U е для всех направлений, кроме направления оптической оси, обуславливает явление двойного лучепреломления в одноосных кристаллах. У двуосных кристаллов имеется два направления, вдоль которых не происходит двойного лучепреломления. Понятие обыкновенного и необыкновенного лучей имеет место пока эти лучи распространяются в кристалле, при выходе из кристалла эти понятия теряют смысл, то есть лучи отличаются только плоскостями поляризаций.
Закон Малюса. Поляризатор, анализирующий в какой плоскости поляризован свет, называется анализатором.
Сквозь анализатор пройдет составляющая параллельная плоскости анализатора, то есть составляющая
Закон Малюса: Интенсивность света, прошедшего через поляризатор, прямо пропорциональна произведению интенсивности падающего плоско поляризованного света I 0 и квадрату косинуса угла между плоскостью падающего света и плоскостью поляризатора. Если на поляризатор падает естественный свет, то интенсивность вышедшего из поляризатора света I 0 равна половине I ест, и тогда из анализатора выйдет
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1837; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.181 (0.008 с.) |

 непригодны для наблюдения дифракции в видимом свете (
непригодны для наблюдения дифракции в видимом свете ( м), но их можно использовать в качестве естественных дифракционных решеток для рентгеновского излучения, т.к. расстояние между атомами в кристаллах одного порядка с
м), но их можно использовать в качестве естественных дифракционных решеток для рентгеновского излучения, т.к. расстояние между атомами в кристаллах одного порядка с  рентгеновского излучения (~10-12— 10-8 м).
рентгеновского излучения (~10-12— 10-8 м).
 (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1’ и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа — Брэггов
(угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1’ и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа — Брэггов (m= 1, 2, 3,...), (14.10)
(m= 1, 2, 3,...), (14.10) и m, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурногоанализа. Формула Вульфа — Брэггов остается справедливой и при дифракции электронов и нейтронов. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются соответственно электронографией и нейтронографией.
и m, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурногоанализа. Формула Вульфа — Брэггов остается справедливой и при дифракции электронов и нейтронов. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются соответственно электронографией и нейтронографией. . Эта зависимость не линейная и не монотонная. Области значения ν, в которых
. Эта зависимость не линейная и не монотонная. Области значения ν, в которых (или
(или  )
)
 (или
(или  ),
),
 ).
). , где
, где  ,
,  . Тогда
. Тогда . Отсюда можно записать:
. Отсюда можно записать: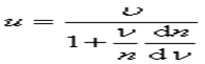 .
.
 .
. , то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.
, то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.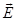 и
и  взаимно перпендикулярны и перпендикулярны направлению распространения. Колебания вектора
взаимно перпендикулярны и перпендикулярны направлению распространения. Колебания вектора 
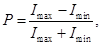

 n12 - показатель преломления второй среды относительно первой. Угол падения (отражения) - угол между падающим (отраженным) лучом и нормалью к поверхности. Плоскость падения - плоскость, проходящая через падающий луч и нормаль к поверхности.
n12 - показатель преломления второй среды относительно первой. Угол падения (отражения) - угол между падающим (отраженным) лучом и нормалью к поверхности. Плоскость падения - плоскость, проходящая через падающий луч и нормаль к поверхности. в различных направлениях.
в различных направлениях.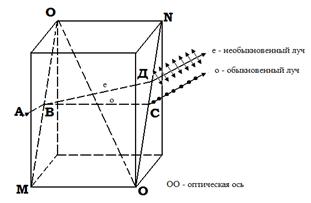 У одноосных кристаллов имеются одно направление, называемое оптической осью, при распространении вдоль которого не происходит разделения на обыкновенный и необыкновенный лучи. Любая прямая параллельная направлению оптической оси будет также являться оптической осью. Любая плоскость, проходящая через оптическую ось и падающий луч, называется главным сечением или главной плоскостью кристаллам.
У одноосных кристаллов имеются одно направление, называемое оптической осью, при распространении вдоль которого не происходит разделения на обыкновенный и необыкновенный лучи. Любая прямая параллельная направлению оптической оси будет также являться оптической осью. Любая плоскость, проходящая через оптическую ось и падающий луч, называется главным сечением или главной плоскостью кристаллам. необыкновенный - нет;
необыкновенный - нет;
 , то для обыкновенного и необыкновенного лучей будут разные показатели преломления n 0 и n е, а так как
, то для обыкновенного и необыкновенного лучей будут разные показатели преломления n 0 и n е, а так как  то можно сказать, что первопричиной двойного лучепреломления является анизотропия диэлектрической проницаемости кристалла. Кристаллы, у которых V е < V 0 (n е > n 0) называются положительными, а у которых V е > V 0 (n е < n 0)называются отрицательными.
то можно сказать, что первопричиной двойного лучепреломления является анизотропия диэлектрической проницаемости кристалла. Кристаллы, у которых V е < V 0 (n е > n 0) называются положительными, а у которых V е > V 0 (n е < n 0)называются отрицательными. Если на анализатор падает плоско поляризованный свет амплитудой Е 0 и интенсивности I 0(
Если на анализатор падает плоско поляризованный свет амплитудой Е 0 и интенсивности I 0(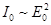 ), плоскость поляризации которого составляет угол φ с плоскостью анализатора, то падающее электромагнитное колебание можно разложить на два колебания; с амплитудами
), плоскость поляризации которого составляет угол φ с плоскостью анализатора, то падающее электромагнитное колебание можно разложить на два колебания; с амплитудами  и
и  , параллельное и перпендикулярное плоскости анализатора.
, параллельное и перпендикулярное плоскости анализатора.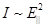 ):
):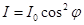 - закон Малюса
- закон Малюса





