
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурные схемы с автоматической коррекцией погрешностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Идея: Какие погрешности мы знаем: Задача: уменьшить или устранить (этим и будем заниматься) возникающие погрешности или, по крайней мере, учесть методами математический статистики (не рассматриваем). Знаем: ООС уменьшает мультипликативную погрешность Для этого существует метод на создании специальных структур, которые: а) Автоматически вырабатывают б) Корректирующий сигнал вид которого зависит от вида погрешности, которую хотим уменьшить.
Пример 1: Пусть есть измерительный преобразователь
X Y + Ш У М ИДЕАЛ:
РЕАЛЬНО:
Разница между реальным случаем и идеальным:
Необходимо собрать следующую цепь:
X Y К выходу Причём между Входной «иксовой» величиной и величиной, подаваемой в коррекционном сигнале обязательно должна быть связь.
Пример 2:
X2 YКОРР ΔX
УСЛОВНО Где ОП – обращённый преобразователь
Случай А) Случай Б) Необходимо доказать, что: А) Б) Ошибка второго порядка малости Необходимо доказать, что
Лекция 16 Теория погрешностей
I. Причины появления погрешностей. II. Погрешности систематические и случайные. III. Описание случайных погрешностей. Понятие доверительного интервала. IV. Обработка ряда прямых наблюдений, содержащих случайные погрешности. V. Идеи суммирования погрешностей. Причины появления погрешностей Так как получить истинные данные об объекте в принципе невозможно, для любых измерений характерна погрешность ΔX:
где XP – расчётное значение измеряемой величины (искомой величины), а QИСТ – истинное значение (то, что есть на самом деле). Иными словами, погрешность – это разница между измеренным и истинным значением. Как уже было говорено (причем, неоднократно) погрешности возникают при любых измерениях и наблюдениях. Представим себе: ИЗМЕРИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
ИЗМЕРИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Кто занимается экспериментом?
Получаем результат измерения с определенной точностью и погрешностью ΔX
А ещё на весь наш измерительный эксперимент воздействуют влияющие факторы
Постоянные во времени или меняющиеся по Постоянные и случайные вместе Случайные определённому закону Причины появления погрешностей: 1) Методические а) несоответствие модели и объекта Пусть объект измерения – генератор.
UВЫХ X = UMAX =?
Подключаем генератор, естественно, к вольтметру…
и вот, что вольтметр показал 0 200 300 V U α = 200 В А нам необходимо было максимальное напряжение UMAX, которое равно:
где К – тот неизвестный коэффициент, при увеличении на который напряжение выдает нам «у-максимальное». И вот тут встаёт проблема выбора дальнейшей модели: - если напряжение – в синусоидальном режиме (как мы предположили в самом начале), то коэффициент К = - если же напряжение не в синусоидальном режиме, то и коэффициент, соответственно, не Вот вам наглядный пример ошибки в выборе модели. б) аналого-дискретные преобразования A Квантованная функция
Ошибка, то есть разность между аналоговой и квантованной функцией существует и равна шагу квантования. 2) Инструментальная погрешность а) погрешность самого прибора Определяется классом точности прибора К и по б) погрешность взаимодействия средства измерения с объектом измерения
Взаимосвязь Пример: Измеряем напряжение на резисторе. Имеем резистор, подключаем, естественно, параллельно, к нему вольтметр…
R UR =? _ Необходимо учитывать несколько условий: во-первых, сопротивление резистора и вольтметра должно подбирать таким образом, чтобы прибор не закорачивал резистор, иначе просто нечего будет измерять, а во-вторых сопротивление вольтметра должно быть очень большим, в идеале - стремиться к бесконечности. 3) Личные особенности экспериментатора и его состояние Экспериментирующий может совершать промахи (грубые погрешности, которые на первой же стадии обработки изымаются из протокола наблюдений) или просто произвести неправильный «отсчет шкалы» прибора. Вот и 0 ошибка XПО ПРИБОРУ = 200 В XВ ПРОТОКОЛЕ = 250 В 4) Вычислительные погрешности, связанные с особенностями ЭВМ и особенностями принимаемых алгоритмов расчёта 5) Погрешности, связанные с влияющими факторами (как то: температура, частота, влажность, давление и проч.) а) постоянные или меняющиеся по определённому закону (получше) б) случайные (пострашнее)
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

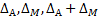
 . Необходимо узнать, как устранить аддитивную погрешность
. Необходимо узнать, как устранить аддитивную погрешность  и погрешность суммарную
и погрешность суммарную  .
.

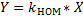


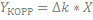

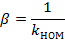

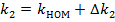
 даже если
даже если 


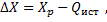

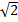 , как известно из курса электрических цепей.
, как известно из курса электрических цепей. .
.


