Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория механизмов и машин и детали машинСодержание книги
Поиск на нашем сайте
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН И ДЕТАЛИ МАШИН Конспект лекций для студентов Направления 6.070104 «Морской и речной транспорт» Специальности «Судовождение», «Эксплуатация судовых энергетических установок» Керчь, 2010г.
УДК 531.8+621.81
Авторы: Курсеитов С.И. к.т.н., доцент цикла «Инженерная механика». КГМТУ. Курсеитова Э.С. зав. лабораторией цикла «Инженерная механика». КГМТУ.
Рецензент: Крестлинг Н.А. к.т.н., доцент кафедры «СЭУ». КГМТУ Гильдебрандт А.И. к.в.н., декан Керченского факультета Херсонского национального технического университета.
Конспект лекций рассмотрен и одобрен на заседании кафедры «Промышленного рыболовства» КГМТУ. Протокол № 3 от 26.09.2008г.
Конспект лекций утвержден на заседании Методической комиссии МФ КГМТУ. Протокол № 3 от 26.11.2008г.
Конспект лекций утвержден на Методическом совете КГМТУ. Протокол № 4 от 20.02.2009г.
© Керченский государственный морской технологический университет Содержание
Введение Целью изучения дисциплины «ТММ и ДМ» для всех специальностей является успешное усвоение общетехнических знаний, которые будут использоваться при изучении других дисциплин, в дальнейшей работе над курсовыми и дипломными проектами (работами), а также в будущей производственной деятельности. Задачи дисциплины дать необходимые общетехнические знания в доступной форме, научить использовать полученные знания при описании основных свойств изучаемых машин и механизмов. Эффективность эксплуатации судовых энергетических установок связана с надежностью и экономичностью работы оборудования. Хорошее усвоение программы курса «ТММ и ДМ» является необходимым условием для освоения других предметов таких как «ДВС» и выполнения диплома. Дисциплина «ТММ и ДМ» базируется на знаниях полученных студентами при изучении курсов высшей математики, физики, теоретической механики, сопротивления материалов, инженерной графики и начертательной геометрии. В результате изучения курса «ТММ и ДМ» студент должен знать: - методики расчета и конструирования механических передач, которые позволяют судовому механику более глубоко понимать работу отдельных узлов машинного отделения и на основании этого уметь обеспечить экономичную и надежную работу оборудования; - теоретическую базу для развития судового оборудования и на основании этого уметь самостоятельно разбираться во все усложняющейся технике и новых научных достижениях и на их основе решать различные практические задачи; уметь: решать задачи с недостающими размерами звеньев. Проводить кинематические исследования механизмов. Решать задачи по расчету механических передач, валов, подшипников качения, элементов привода. Решать задачи кинематического расчета привода.
Раздел 1. Теория механизмов и машин.
Лекция 1. Задачи курса. Машина, классификация.
Рождением науки о машинах и механизмах можно считать конец XVIII в. Теория механизмов и машин оформилась как самостоятельная ветвь науки в XX в. Достойный вклад в развитие ТММ внес гениальный ученый – М.В. Ломоносов, разработавший конструкции машин для производства стекла и испытаний материалов. Его научные открытия послужили источником творчества русских умельцев, изобретателей и конструкторов: И.И. Ползунова – творца паровой машины; И.П. Кулибина – создателя механизма протеза; часов – автоматов; «самокатки», которая носила черты будущих автомобилей, она имела устройства для переключения зубчатых передач и свободного хода, тормоз, управление колесами; Е.А.Черепанов, построивший первый в России паровоз. В это же время протекала плодотворная деятельность величайшего математика и механика Л. Эйлера, разработавшего теорию плоских зацеплений и предложившего эвольвентный профиль зубьев колеса. К середине XIX в. в России выросла плеяда талантливых ученых, заложивших основы современной теории механизмов и машин. П.Л. Чебышев, которому принадлежит ряд оригинальных исследований, посвященных синтезу механизмов, теории зубчатых зацеплений, структуре плоских механизмов. Он создал схемы свыше 40 различных механизмов. Н.Е. Жуковскому принадлежит также ряд работ, посвященных решению задач динамики машин (теория о жестком рычаге). Профессор Л.Я. Ассур разработал строгую и научную классификацию плоских шарнирно – рычажных механизмов. На протяжении более сорока лет в XX веке в Москве плодотворно работал в области теории механизмов и машин академик И.И. Артоболевский. Его труды теории структуры, по теории пространственных механизмов, синтезу и динамике машин и механизмов стали классическими. Он создал новые методы проектирования механизмов и динамики машин. В ТММ изложены методы исследования и проектирования механизмов и машин. Под исследованием механизмов и машин понимают изучение движения звеньев машин и их точек. Проектирование, или синтез, механизмов представляет разработку рациональных методов определения параметров механизмов и машин по заданным функциям их движения. ТММ есть наука, изучающая структуру, кинематику и динамику механизмов в связи с их анализом и синтезом. Анализ механизмов состоит в исследовании структурных, кинематических и динамических свойств механизма по заданной его схеме. Синтез механизма – в проектировании схемы механизма по заданным его свойствам. Этот курс является фундаментальным в системе подготовки инженеров. Структура и содержание курса предусматривают обязательное последовательное изучение составляющих его дисциплин и их разделов при творческой направленности лабораторных работ и курсового проектирования. Задача изучения курса: научить студентов методам исследования механизмов и машин, умению технически грамотно выполнять расчеты и рационально конструировать детали, сборочные единицы и машины в целом.
Машина, классификация. Машина – есть устройство, выполняющее механические движения для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека. В зависимости от основного назначения (какой вид преобразования преобладает) различают энергетические, технологические, транспортные и информационные машины. Энергетические машины предназначены для преобразования любого вида энергии в механическую (и наоборот). К ним принадлежат, например, электродвигатели, турбины, ДВС, паровые машины, электрогенераторы, компрессоры. Машины для преобразования материалов подразделяются на технологические и транспортные. В технологических машинах под материалом подразумевается обрабатываемый предмет, который может быть в твердом, жидком и газообразном виде. Преобразование материалов в этих машинах состоит в изменении его размеров, формы, свойств или состояния. Примеры технологических машин: металлообрабатывающие станки, прокатные станки, ткацкие станки, упаковочные машины. В транспортных машинах под материалом понимается перемещенный предмет. Примеры транспортных машин: автомобили, тепловозы, самолеты, вертолеты, подъемники, краны, транспортеры. В тех случаях, когда транспортная машина предназначена для перемещения людей, под материалом, конечно, понимается кабина лифта, вагон, шасси автомобиля и т.д. Машины, предназначенные для получения и преобразования информации, называются информационными. Если информация в виде чисел, то информационная машина называется счетной или вычислительной. Примеры счетных машин: арифмометры, механические интеграторы, бухгалтерские машины. ЭВМ, строго говоря, не является машиной, т.к. в ней механические движения служат лишь для выполнения операций. Итак, основным признаком, отличающим машину от других устройств, является выполнение механических движений, - отсюда и происходит термин «машина» (от лат. machine). Машина, в которой все преобразования энергии, материалов и информации выполняются без непосредственного участия человека, называется машиной – автоматом. Совокупность машин – автоматов, соединенных между собой автоматическими транспортными устройствами и предназначенных для выполнения определенного технологического процесса, образуют автоматическую линию. Машина, особенно машина – автомат, при правильном ее использовании облегчает труд человека, увеличивает производительность труда и обеспечивает высокое качество выполнения рабочего процесса.
Кинематические схемы машин.
Рис.1.1. Тестосмесительная машина
1
Рис.1.2. Машина для ворошения сена.
Рис.1.3. Снегоуборочная машина.
Лекция 2. Механизмы, классификация.
Механизм представляет собой совокупность связанных звеньев, предназначенных для передачи и преобразования движения одного или нескольких звеньев (входных, ведущих) в определенные движения остальных звеньев (выходных, ведомых). Плоским механизмом называется механизм, точки звеньев которого описывают траекторию, лежащие в параллельных плоскостях.
Основные виды плоских механизмов: Рычажные механизмы.
Рычажный механизм, звенья которого образуют только вращательные пары, называется шарнирным.
Иногда в механизмах шарнир может соединять три звена, тогда будет иметься не одна, а две кинематические вращательные пары.
Кулисные механизмы. Рычажный механизм, в состав которого входит кулиса, называется кулисным. (Кулиса – звено рычажного механизма, вращающееся вокруг неподвижной оси и образующие с другим подвижным звеном поступательную пару). Кулисно – ползунный механизм – рычажный четырехзвенный механизм, содержащий кулису 1 и ползун 3, шатун 2, неподвижную направляющую 4. (Рис.2.4).
Кулисно – ползунный механизм служит для преобразования качательного движения кулисы 1 в поступательное движение ползуна 3 или, наоборот, поступательное движение ползуна 3 в качательное движение кулисы 1. Кулиса 1 и ползун 3 взаимодействуют посредством шатуна 2, связанного с кулисой поступательной парой, а с ползуном 3 – вращательной парой. Звено 4 – неподвижная стойка. Кривошипно – кулисный механизм – рычажный четырехзвенный механизм, в состав которого входят кривошип 1 и кулиса 3 (см. рис.2.5). Кривошипно – кулисный механизм служит для преобразования вращательного движения кривошипа 1 во вращательное движение кулисы 3 и наоборот, движения кулисы во вращение кривошипа. Звено 4 - неподвижная стойка.
Кулачковые механизмы. Кулачковым механизмом называется механизм, в состав которого входит кулачок. Кулачковый механизм позволяет преобразовать вращательное движение кулачка 1 в поступательное движение толкателя 2 (рис.2.6) или в качательное движение коромысла 2 (рис.2.7), неподвижное звено – стойка 3.
Зубчатый механизм.
Зубчатым механизмом (рис.2.8.) называется передаточный механизм, в котором подвижными звеньями 1 и 2 являются зубчатые колеса, образующие со стойкой 3 цилиндрические вращательные пары, а между собой высшую кинематическую пару. В практике часто применяют комбинированные механизмы, состоящие из двух и более механизмов различного вида. Кинематическая схема механизма – это графическое изображение последовательности соединения звеньев в кинематические пары с указанием размеров звеньев. Кинематическая цепь – система звеньев, связанных между собой кинематическими парами.
Звенья механизмов. Каждая подвижная деталь или группа деталей, образующая одну жесткую подвижную систему тел называется подвижным звеном механизма. Все неподвижные детали образуют одну жесткую неподвижную систему тел, называемую неподвижным звеном или стойкой (корпусом). Таким образом, в любом механизме имеется одно неподвижное звено и одно или несколько подвижных звеньев. Входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Входное звено соединено с двигателем либо с выходным звеном другого механизма. Выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм. Выходное звено соединено с генератором, либо с исполнительным устройством (рабочим органом), либо со сходным звеном другого механизма.
Лекция 3. Кинематические пары
Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Соприкосновение звеньев может происходить на поверхности, линии и точке. Если соприкосновение происходит по линии и точке, то кинематическая пара называется высшей. Если соприкосновение происходит по поверхности, то кинематическая пара называется низшей. К низшим кинематическим парам принадлежат: вращательная, поступательная, цилиндрическая, сферическая и плоскостная. Различают кинематические пары по числу степеней свободы H (с одной, двумя, …, пятью) и называют их соответственно одноподвижной, двухподвижной,..., пятиподвижной кинематическими парами. Соответственно этому кинематическая пара имеет 5,4,…,1 связи S. Их обозначают как кинематические пары 1;2;3;4;5 класса (класс соответствует числу наложенных связей). Класс кинематической пары определяется по формуле: S = 6 – H (1). Основные виды звеньев Таблица 3.2.
Определение звеньев. 1. Кривошип – вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси; 2. Шатун – звено рычажного механизма, не образующее кинематическую пару со стойкой; 3. Ползун - звено рычажного механизма, образующее поступательную пару со стойкой; 4. Коромысло – вращающееся звено кулачкового механизма, которое может совершать неполный оборот вокруг неподвижной оси; 5. Кулиса – звено рычажного механизма, вращающееся вокруг неподвижной оси и образующее с другим неподвижным звеном поступательную пару; 6. Кулачек – звено, выполненное в виде поверхности переменной кривизны; 7. Зубчатое колесо – зубчатое звено с замкнутой системой зубьев, обеспечивающее непрерывное движение другого зубчатого колеса.
Кинематические цепи. Система звеньев соединенных с помощью кинематической пары называется кинематической цепью.
а) замкнутая б) разомкнутая с) замкнутая д) разомкнутая простая простая сложная сложная
В зависимости от строения различают замкнутые и незамкнутые кинематические цепи. В замкнутой кинематической цепи а) и с) каждое звено входит не менее чем в две кинематические пары, в незамкнутой (открытой) цепи б) и в) имеются звенья, входящие лишь в одну кинематическую пару. Таким образом, механизм – это кинематическая цепь при заданном движении одного или нескольких звеньев относительно любого из них все остальные звенья движутся определенным образом. Кинематические цепи классифицируют также по внешнему признаку, условно подразделяя их на плоские и пространственные, на простые и сложные. Простой называется кинематическая цепь, у которой каждое звено входит в соединение с другим звеном с помощью одной или двух кинематических пар. В противном случае цепь называется сложной. Лекция 4. Лекция 5. Нарезание зубьев. Наиболее просто и точно профиль зуба, сопряженный заданному, получается при нарезании зубчатых колес на зубофрезерных и зубодолбежных станках, работающих по методу обкатывания или огибания. Режущий инструмент, имеющий форму зубчатого колеса, снимает стружку, перемещаясь параллельно образующей цилиндрической заготовки, и формирует впадину между будущими зубьями. После обратного хода инструмент и заготовки поворачивают вокруг своих осей на малые углы, обратно пропорциональные числам их зубьев, как если бы они были зацепляющими колесами. При новом режущем ходе инструмента срезается следующая стружка с заготовки в той же впадине и т.д. В результате профиль зуба получается близким к точному теоретическому профилю, который есть огибающая последовательных положений зуба инструмента относительно заготовки. Таким образом происходит нарезание и тогда, когда инструмент имеет форму рейки, поскольку рейку можно рассматривать как зубчатое колесо с бесконечно большим числом зубьев.
Дуга зацепления. Дугой зацепления называют дугу начальной окружности, которая проходит мимо полюса Р за время зацепления одной пары сопряженных профилей. Длину k дуги зацепления определяют по формуле: k = где l – длина активной части линии зацепления.
Коэффициент перекрытия. Коэффициентом перекрытия называют отношение длины k дуги зацепления к длине шага Рt по начальным окружностям колес: ε = Pt cosα = P cosαo = Po (18); Pt = mπ (18), Где Ро – основной шаг, т.е. шаг зацепления на основных окружностях, то ε = Формулой (19) удобно пользоваться тогда, когда зацепление двух колес уже вычерчено. В этом случае длину l можно измерить на чертеже. Лекция 6. Раздел 2. Детали машин.
Лекция 7
Основные задачи курса ДМ. Связь курса с общетехническими и специальными дисциплинами. Понятие детали и узла. Основные критерии работоспособности.
Машины в зависимости от сложности и габаритов разделяются на некоторое число сборочных единиц (узлов) и деталей. Д е т а л ь – изделие, изготовленное из однородного, по наименованию и марке материала, без применения сборочных операций. С б о р о ч н а я е д и н и ц а (узел) – изделие, составные части которого подлежат соединению между собой на предприятии-изготовителе сборочными операциями. Различают детали машин о б щ е г о и с п е ц и а л ь н о г о назначения. К деталям машин о б щ е г о назначения относятся: элементы разъемных и неразъемных соединений; части передач зацеплением и трением; валы и оси. К узлам о б щ е г о назначения относятся: подшипники качения, подшипники скольжения, муфты, редукторы, коробки скоростей. К деталям машин с п е ц и а л ь н о г о назначения относятся детали, встречающиеся только в отдельных видах машин. К ним относятся такие детали, как поршень, клапан, шпиндель и т.п. Проектирование этих деталей изучается в специальных дисциплинах – «Двигатели внутреннего сгорания», «Металлорежущие станки» и т. д. Курс «Детали машин» формирует будущего инженера как специалиста. Курс «Детали машин» с курсовым проектом реализует и завершает общетехническую подготовку студента. Курс «Детали машин» базируется на общенаучных и общеинженерных дисциплинах. Он заимствует математический аппарат исследований из математики, методы анализа сил, напряжений и деформации – из теоретической механики и сопротивления материалов. Свойства конструкционных материалов – из материаловедения, методы прогнозирования ресурса деталей и узлов машин – из теории надежности. Основные задачи курса: – Изучение конструкций деталей, узлов и агрегатов; – Изучение основ теории совместной работы деталей и методов их расчета; – Развитие навыков конструирования и технического творчества. В инженерной практике встречаются два вида расчета: проектный и проверочный. П р о е к т н ы й р а с ч е т – предварительный, упрощенный расчет, выполняемый в процессе разработки конструкции детали (машины) в целях определения ее размеров и материала. П р о в е р о ч н ы й р а с ч е т – уточненный расчет известной конструкции, выполняемый в целях проверки ее прочности или определения норм нагрузки.
Лекция 8
Диаметр вершин зубьев
da = d + 2ha= mz +2m = m(z+2) (4)
Диаметр впадин зубьев
df =d-2hf =mz-2 . 1,25m =m(z-2,5) (5)
Межосевое расстояние
d1+d2 m aw = ¾¾¾ = ¾¾ (z1+z 2) (6) 2 2 ГОСТ 1643 – 81 на допуски для цилиндрических зубчатых колес и передач установлены 12 степеней точности обозначаемых цифрами. 1степень – наивысшая. Для каждой степени точности установлены нормы: кинематической точности, плавности работы и контакта зубьев колес и передач. В машиностроении зубчатые передачи общего назначения изготовляют по 6 – 9-й степеням точности.
Рис.8.6
Силу нормального давления Fn разложим на две взаимно перпендикулярные составляющие Ft и Fr, которые называются окружной и радиальной силами. Ft = Fncosa (7)
Fr = Fnsina (8)
2T Ft = ¾¾ (9) d
Fr = Fttga (10)
a = 20o – угол зацепления
Давление на валы и опоры цилиндрической прямозубой передачи.
Ft1
l1 l2
RAY . l1
Рис.8.7
В горизонтальной плоскости ZOX:
SMA=0; -Ft1 . l1+RBX(l1+l2)=0
Ft1 . l1 RBX = ¾¾¾ l1+l2
SMB=0; Ft1 . l2 – RAX(l1+l2)=0
Ft1 . l2 RAX= ¾¾¾ l1+l2 В вертикальной плоскости:
SMA=0; Fr1 . l1-RBY(l1+l2)=0
Fr1 . l1 RBY = ¾¾¾ l1+l2
SMB=0; -Fr1 . l2 – RAY(l1+l2)=0
Fr1 . l2 RAY= ¾¾¾ l1+l2
Лекция 9 Рис.9.2
Pn Нормальный модуль mn = ¾¾ p
Pt Pn mn Окружной модуль mt = ¾¾ т.к. Pt = ¾¾, то mt = ¾¾ (11) p cosb cosb
Размеры зубьев косозубого колеса определяют по нормальному модулю, т.е. h = ha+ hf = mn+ 1,25mn = 2,25 mn
Диаметр делительной окружности mnz d = mtz = ¾¾ (12) Cosb
Диаметр вершин зубьев
mnz z da = d + 2ha= d +2mn = ¾¾+2mn = mn (¾¾ + 2) (13) cosb cosb
Диаметр впадин зубьев
mnz z df = d-2hf =d-2,5mn = ¾¾-2,5mn = mn (¾¾-2,5) (14) cosb cosb Межосевое расстояние
mt mn aw = ¾¾ (z1+z 2) = ¾¾¾ (z1+z 2) (15) 2 2 cosb
Шевронные передачи. Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями, называется ш е в р о н н ы м. Из технологических соображений шевронные колеса изготовляют двух типов с дорожкой посредине колеса (а) и без дорожки (б).
Fa/ Fa/
F/ F/
a) б)
Рис.9.3
В шевронном колесе осевые силы Fa/ на полушевронах, направлены в противоположные стороны, взаимно уравновешиваются внутри колеса и на валы и опоры валов не передаются. Поэтому у шевронных колес угол наклона зубьев принимают в пределах =25о...40о, в результате чего повышается прочность зубьев, плавность работы передачи и ее нагрузочная способность. Поэтому шевронные колеса применяют в мощных быстроходных закрытых передачах. Недостатком шевронных колес является высокая трудоемкость и себестоимость изготовления. Эквивалентные колеса.
Прочность зуба косозубого колеса определяется его формой и размерами в нормальном сечении и длиной зуба.
колесо
b
d
n Рис.9.4
В сечении nn – нормальное сечение делительной цилиндрической поверхности этого колеса представляет собой эллипс с полуосями d d е = ¾¾¾ и c = ¾¾, 2cosb 2 где d – диаметр делительной окружности. Как известно из аналитической геометрии, максимальный радиус кривизны эллипса е2 d ru= ¾¾ = ¾¾¾ с 2cos2b Этот радиус кривизны принимаем за радиус делительного цилиндра эквивалентного колеса, тогда его диаметр d du = ¾¾¾ cos2b
Подставив в формулу du = mnzu
mnz d = ¾¾¾, cosb <
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.012 с.) |




 Рычажным механизмом называется механизм, звенья которого образуют только вращательные и поступательные кинематические пары. На рис.2.1. показана кинематическая схема кривошипно – ползунного механизма.
Рычажным механизмом называется механизм, звенья которого образуют только вращательные и поступательные кинематические пары. На рис.2.1. показана кинематическая схема кривошипно – ползунного механизма.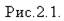 У такого ползунного механизма входное звено – кривошип, а выходное – ползун. Механизм содержит три подвижных звена (кривошип – 1, шатун – 2 и ползун – 3), одно неподвижное, принятое за стойку (корпус) – 4.
У такого ползунного механизма входное звено – кривошип, а выходное – ползун. Механизм содержит три подвижных звена (кривошип – 1, шатун – 2 и ползун – 3), одно неподвижное, принятое за стойку (корпус) – 4.
















 (16),
(16), (17),
(17),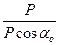 =
=  (19).
(19).

 z 0
z 0

 RAX RBX x
RAX RBX x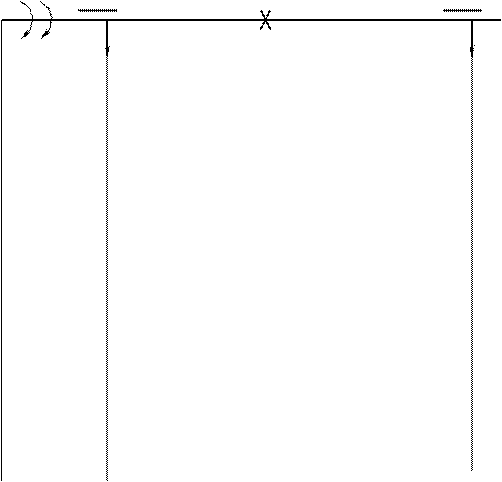


 A Fr1 B
A Fr1 B
 w1 T1 RAY RBY
w1 T1 RAY RBY



 RAX . l1
RAX . l1

 My(Н . м)
My(Н . м)











 MX(Н . м)
MX(Н . м)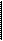






 MZ(Н . м) T1
MZ(Н . м) T1





 b
b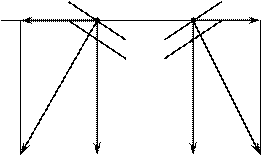





 Ft/ Ft/
Ft/ Ft/
 Эквивалентное с
Эквивалентное с

 е ru
е ru

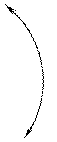 n 90o
n 90o