
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи математичного аналізу
Сталі та змінні величини
Величина називається сталою, якщо її значення не змінюється з бігом часу, і змінною, якщо змінюється. Змінна величина називається обмеженою, якщо її значення за модулем виявляється менше деякого додатного числа за весь час спостереження. У противному разі величина називається необмеженою. Змінна величина називається зростаючою, якщо її значення з бігом часу не спадає. Змінна величина називається спадною, якщо її значення з бігом часу не зростає. Зростаючи та спадні величини називаються монотонними.
Нескінченно малі величини та їх властивості
Змінна величина називається нескінченно малою, якщо її значення за абсолютною величиною в процесі змінювання стає і надалі залишається менше будь-якого додатного числа. Зауважимо, що єдина стала нескінченно мала величина це Сума, різниця, добуток нескінченно малих величин є нескінченно малі величини. Відношення нескінченно малих величин може бути будь-якою величиною. У випадку відношення нескінченно малих величин ми кажемо, що у нас є невизначеність вигляду Границі змінних величин та їх властивості Стала величина Відзначимо, що сталі і змінні величини ми будемо позначати першими літерами латинського алфавіту Відмітимо наступні властивості границь. Кожна величина має не більше однієї границі (може не мати жодної). Границя суми змінних величин дорівнює сумі їх границь, якщо останні існують, тобто якщо Аналогічні властивості мають місце для різниці та добутку. Сталий множник можна виносити з-під знаку границі.
Границя відношення змінних величин дорівнює відношенню їх границь, якщо останні існують, та якщо границя знаменника відмінна від нуля.
Зокрема, границю відношення двох многочленів, якщо границя знаменника відмінна від Приклад. Якщо границі чисельника та знаменника дорівнюють
Приклад.
Змінна величина називається нескінченно великою, якщо в процесі змінювання вона за модулем стає і надалі залишається більше будь-якого додатного числа. Позначення: Величина, обернена до нескінченно великої, є нескінченно малою, і величина, обернена до нескінченно малої, що не обертається на Приклад. Для знаходження границі відношення двох многочленів, якщо аргумент прямує до нескінченності, треба розділити чисельник та знаменник на старший степінь незалежної змінної. Приклад. Знайти Розв'язання.
Функція Кажуть, що на деякій множині дійсних чисел задана функція Елементарні функції Елементарними функціями називають: степеневі Кожна елементарна функція має природну область визначення. Приріст Нехай задана функція Неперервність функції Функція
Еквівалентні означення неперервності: 1. 2. Можна довести, що кожна елементарна функція неперервна у своїй натуральній області визначення. Неперервність функцій використовується при обчисленні границь. Приклад. Знайти Розв'язання. Для знаходження границі треба домножити чисельник і знаменник на вираз спряжений до чисельника
При розв'язанні прикладу ми скористалися неперервністю функції Перша чудова границя Границя відношення синуса нескінченно малого кута до того ж кута, виміряного у радіанах, існує і дорівнює одиниці.
З першої чудової границі легко отримати наступні дві формули, корисні при розв'язанні прикладів:
Приклад. Знайти границю Розв'язання.
Друга чудова границя Виявляється, що змінна величина
де Інша форма запису другої чудової границі, що зручна при обчисленнях:
Натуральний логарифми Логарифм з основою
Похідна
Похідною функції
Операція знаходження похідної називається диференціюванням функції; функція яка має похідну у цій точці, називається диференційованою у цій точці. Еквівалентне позначення похідної:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.51.3 (0.019 с.) |
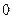 .
. .
. називається границею змінної величини
називається границею змінної величини  і позначається
і позначається 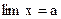 , якщо їх різниця
, якщо їх різниця  – нескінченно мала величина.
– нескінченно мала величина.


 і
і 




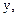
 а нескінченно малі величини першими літерами грецького алфавіту:
а нескінченно малі величини першими літерами грецького алфавіту: 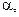


 , то
, то  .
. .
. ,
,  .
. .
. .
. .
. .
. .
.
 , якщо кожному значенню
, якщо кожному значенню 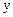 . При цьому
. При цьому  , показникові
, показникові  , многочлени
, многочлени  , раціональні дроби
, раціональні дроби  , тригонометричні:
, тригонометричні:  ,
, 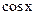 ,
,  ,
,  , обернені тригонометричні:
, обернені тригонометричні:  ,
,  ,
,  ,
,  , логарифмічні
, логарифмічні  ,.
,.  ,
, 
 і обчислимо функцію при цьому значенні
і обчислимо функцію при цьому значенні  . Потім візьмемо друге значення аргументу
. Потім візьмемо друге значення аргументу  і обчислимо
і обчислимо  . Тоді приростом незалежної змінної ми називаємо
. Тоді приростом незалежної змінної ми називаємо  , а приростом функції
, а приростом функції  .
. , якщо у цій точці має місце рівність
, якщо у цій точці має місце рівність .
. . Неперервність дозволяє переходити до границі під знаком функції.
. Неперервність дозволяє переходити до границі під знаком функції. . Функція неперервна, якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції.
. Функція неперервна, якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції. .
.
 .
. - перша чудова границя.
- перша чудова границя.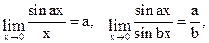 де
де 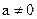 і
і  .
. .
. .
.  має границю, яка позначається
має границю, яка позначається  і називається другою чудовою границею:
і називається другою чудовою границею: ,
, - стала Ейлера – одна з найважливіших констант у математиці.
- стала Ейлера – одна з найважливіших констант у математиці. .
. пишуть
пишуть  .
.
 ,
,  ,
,  ,
,  .
.


