
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні твимоги до виконання і оформленняСтр 1 из 9Следующая ⇒
ІНДИВІДУЛЬНІ ЗАВДАННЯ У ФОРМІ КОНТРОЛЬНИХ РОБІТ
Контрольна робота №1 передбачена для заочної форми навчання. Мета виконання: закріплення одержаних теоретичних і практичних знань щодо вирішення завдань з вищої математики, опанування навичками роботи з науково-методичною, науково-технічною, довідковою літературою. Варіант контрольної роботи обирається студентом відповідно до останньої цифри залікової книжки. Приблизний обсяг роботи 8-10 стор., загальний обсяг часу на виконання КР – 30 годин.
Примітки: Завдання №1–160 з [1], а завдання №161–380 з [2], що наведені в пункті «МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ» цих методичних вказівок.
ЗАГАЛЬНІ РЕКОМЕНДАЦІЇ
1. В процессе изучения курса математики заочник должен выполнить ряд контрольных работ по варианту, номер которого совпадает с последней цифрой его учебного номера (шифра). 2. Не следует приступать к выполнению контрольной работы, не решив достаточного количества типовых задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольной работы вызывается тем, что заочник не выполнил это требование. 3. Контрольные работы должна быть выполнены самостоятельно. Несамостоятельно выполненная работа не приводит к усвоению учебного материала, в результате чего заочник не приобретает необходимых знаний и может оказаться неподготовленным к экзамену. 4. Выполненная контрольная работа предоставляется на рецензию преподавателю. 5. Прорецензированную контрольную работу вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированной контрольной работы заочник не допускается к её защите и сдаче экзамена.
Основні твимоги до виконання і оформлення Контрольних робіт
1. Каждая работа должна быть оформлена отдельно на бумажном или электронном носителе. При использовании бумажного носителя контрольную работу следует выполнять либо в отдельной школьной тетради в клетку, либо на листах формата А4, чернилами темно-синего, фиолетового или черного цвета, оставляя широкие (не меньше 3 см) все четыре поля (слева, справа, сверху, снизу) для замечаний рецензента. В конце рекомендуется оставлять несколько чистых листов для исправлений и дополнений в соответствии с указаниями рецензента. Контрольная работа может бить оформлена и сдана на электронном носителе. Подробные требования по оформлению приведены в Приложении. 2. Перед решением каждой задачи нужно привести полностью ее условие. Переход от текста задачи к решению выделяется словом «Решение». 3. Следует придерживаться той последовательности при решении задач, в какой они даны в задании, строго сохраняя при этом нумерацию примеров (задач). 4. Не допускается замена задач контрольного задания другими. 5. Решения задач должны сопровождаться развернутыми пояснениями; нужно привести в общем виде используемые формулы с объяснением употребляемых обозначений. 6. Чертежи к задачам контрольной работы должны быть выполнены в прямоугольной системе координат в полном соответствии с данными условиями задач и теми результатами, которые получены. 7. Если вычисления, выполняемые при решении задач приближенные, то следует придерживаться правил приближенных вычислений. 8. В конце работы приводится список использованной литературы (указывают автора, название, издательство, год издания). Ставится дата окончания работы и подпись. 9. На обложку тетради наклеивается специальный бланк (наберите форму бланка на компьютере согласно Приложению) на котором следует указать фамилию, имя, отчество (полностью), факультет, специальность, курс, шифр (номер зачетной книжки), вариант и номер контрольной работы. Если работа получила в целом положительную оценку («Допускается к защите»), но в ней есть отдельные недочеты (указанные в рецензии в тетради), то нужно сделать соответствующие исправления и дополнения в той же тетради (после имеющихся решений и записи «Работа над ошибкам и») и предъявить на экзамене или собеседовании. Если работа не зачтена, ее необходимо в соответствии с требованиями рецензента частично или полностью переделать. В случае отсутствия прямого указания рецензента на то, что студент может ограничиться предоставлением исправленных решений отдельных задач, вся работа должна выполняться заново.
Повторную работу надо выполнить в новой тетради с надписью на обложке «Повторная», с указанием фамилии рецензента, которым работа была ранее не зачтена, вместе с не зачтенной работой и рецензией направить снова в академию.
Захист контрольної роботи
Защита прорецензированной и допущенной к защите контрольной работы проводится в виде собеседования. В процессе защиты заочник должен подтвердить самостоятельность выполнения контрольной работы. После успешной защиты контрольная работа считается зачтенной, и студент допускается к сдаче экзамена. Во время собеседования проверяется самостоятельность выполнения работы, выявляются знания основных теоретических положений программы изучаемого курса, охватываемого данной контрольной работой, умение решать подобные задачи и примеры. Поэтому к собеседованию рекомендуется тщательно разобрать методы решения задач и повторить соответствующий теоретический материал, формулы. При положительном результате собеседования контрольная работа зачитывается, а на обложке тетради преподаватель делает соответствующую запись. Студенты, не получившие зачета хотя бы по одной из контрольных работ, к экзамену не допускаются. Зачтенные работы отбираются и не подлежат возвращению после успешной их защиты.
МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ
1. Методичні вказівки та контрольні завдання з вищої математики (для студентів заочної форми навчання усіх спеціальностей). Частина перша / А.І. Колосов, С.О. Станішевський та ін. – Х.: ХНАМГ, 2006. 2. Методичні вказівки та контрольні завдання з вищої математики (для студентів заочної форми навчання усіх спеціальностей). Частина друга / А.І. Колосов, М.Й. Кадець та ін. – Х.: ХНАМГ, 2006.
ЛІТЕРАТУРА Основна
1. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1985. – 383 с. 2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – СПб.: Лань, 2003. – 736 с. 3. Бізюк В.В., Якунін А.В. Спеціальні розділи вищої математики для електротехніків – Харків: ХНАМГ, 2008. – 300 с. 4. Вища математика для електротехніків: у 3-х модулях / С.О. Станішевський, А.В. Якунін, В.С. Ситникова та ін.; Харк. нац. акад. міськ. госп-ва. – Х.: ХНАМГ, 2009. – Модуль 1: Аналітична геометрія на площині. Вступ до математичного аналізу. Диференціальне числення функцій однієї змінної. Лінійна та векторна алгебра. Площина та пряма у просторі. Комплексні числа та функції / С.О. Станішевський, А.В. Якунін, В.С. Ситникова. – 2009. – 308 с. Модуль 2: Інтегральне числення функцій однієї змінної. Диференціальні рівняння. Операційне числення. Елементи варіаційного числення / С.О. Станішевський, А.В. Якунін, А.О. Володченко. – 2010. – 350 с.
Модуль 3: Числові та функціональні ряди. Функції декількох змінних. Елементи теорії поля. Криволінійні та поверхневі інтеграли. Рівняння математичної фізики / В.В. Бізюк, А.В. Якунін. – 2011. – 383 с. 5. Вища математика. У 2ч. / За ред. П.П. Овчинникова. – К.: Техніка, 2003. 6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1,2. – М.: Наука, 1997. – Ч.1 – 303 с., Ч.2 – 415 с. 7. Дубовик В.П., Юрик І.І. Вища математика. – К.: А.С.К., 2003. – 648 с. 8. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1975. – 272 с. 9. Пак В.В., Носенко Ю.Л. Вища математика. – Донецьк: Сталкер, 2003. – 495 с. 10. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2 т. – М.: Наука, 1985. 11. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. – М.: Наука, 1968. – 336 с.
Додаткова 1. Архіпова О.С., Протопопова В.П., Пахомова Є.С. Посібник для розв’язання типових завдань з курсу «Вища математика». – Харків: ХНАМГ, 2008р. − 210 с. 2. Вороновська Л.П., Пахомова Є.С., Шульгіна С.С. Методичні вказівки до вирішення задач з вищої математики (для студентів 1 курсу усіх спеціальностей Академії). Частина 1. – Х.: ХНАМГ, 2012. – 84 с. 3. Вороновська Л.П., Пахомова Є.С., Шульгіна С.С. Методичні вказівки з вищої математики (для самостійної роботи студентів 2 курсу всіх спеціальностей академії). Частина 3. –Х.: ХНАМГ, 2012. – 66 с. 4. Печеніжський Ю.Є., Станішевський С.О. Посібник для розв’язування задач з вищої математики, – Х.: ХДАМГ, 2003. – 100 с. 5. Шульгіна С.С., Вороновська Л.П., Пахомова Є.С. Методичні вказівки з вищої математики для самостійної роботи студентів 1 курсу всіх спеціальностей, частина 2. – Х.: ХНАМГ, 2012. – 112 с.
ДОДАТОК
На титульном листе контрольной работы, согласно приведенного образца (рис. 1), должны быть указаны: номер контрольной работы, номер группы, фамилия, имя, отчество (полностью) студента, учебный номер (шифр), номер варианта, дата отправления контрольной работы, обычный почтовый адрес и электронный адрес (при наличии) для связи со студентом. При использовании электронного носителя контрольная работа должны быть выполнены в редакторе «Microsoft Word» версии 97–2003 (файлы с расширением doc, но не docx) шрифтом «Times New Roman» с автоматическим переносом слов. Язык – украинский, русский, английский. Размер бумаги: А5 148´210 мм. Ориентация – книжная. Одна страница на листе. Все четыре поля (слева, справа, сверху, снизу) по 2,0 см. Расстояния от края до колонтитулов – 1,2 см. Межстрочный интервал - одинарный. Выравнивание – по ширине. Отступы слева и справа отсутствуют (0 см). Абзац (красная строка) – 0,9 см. Нумерация страниц – внизу от центра, начиная со второй страницы. Титульный лист надо включить в общую нумерацию (первая страница).
Размер шрифта – 11 пт. Шрифт – обычный прямой (без подчеркивания и других эффектов). Заглавие раздела набирается полужирным шрифтом (прямым) без точки в конце и отделяется от основного текста сверху и снизу дополнительным интервалом 6 пт. Слова в заглавии не переносятся. Выравнивание – по центру.
Условие задачи отделяется от основного текста сверху и снизу дополнительным интервалом 3 пт. Слова в условии задачи не переносятся. Переменные в тексте набираются в редакторе формул Microsoft Equation 3.0 (для сохранения идентичности с переменными в формулах). Размер переменных (как и в формулах) – 12пт (на 2пт больше, чем основного текста). Формулы набираются редактором формул Microsoft Equation 3.0. Каждая формула набирается построчно (каждая строка набирается отдельно) и каждая строка располагается в отдельном абзаце с красной строки 0,9 см. Каждая строка формулы отделяется сверху и снизу дополнительным интервалом 3 пт. В редакторе Microsoft Equation 3.0 в элементе меню STYLE, DEFINE определить шрифт «Times New Roman» для первых трех стилей (сверху вниз) и для двух последних, а для стилей L.C.Greek, U.C.Greek, Symbol установить шрифт «Symbol». Курсивом (italik) отметить два стиля: Text и Variable (Текст, Переменная), а все остальные стили – обычный шрифт (прямой). В редакторе Microsoft Equation 3.0 в элементе меню SIZE, DEFINE установить следующие размеры (сверху вниз): основной – 12 пт; крупный индекс – 8 пт; мелкий индекс – 6 пт; крупный символ – 16 пт; мелкий символ – 10 пт. Примечание 1. При наборе формулы (внутри редактора Microsoft Equation 3.0) следует отдавать предпочтение (в случае наличия альтернативных возможностей) набору с клавиатуры, а не “Шаблонам”. Прежде всего это касается самых внутреннихскобок (), [ ], { }, и черточек / для деления, | для модуля, \ для ограничения, поскольку позволяет уменьшить высоту формулы (при условии, что знаки по высоте охватывают соответствующее выражение). Примечание 2. Если это существенно не ухудшает уровень “читабельности”, нужно стремится к уменьшению высоты формулы (при условии, что знаки скобок, суммы, интеграла по высоте охватывают соответствующее выражение), “растягивая” запись за счет применения (см. Шаблоны Microsoft Equation 3.0): 1) для деления (дроби) вместо черты Рисунки и таблицы (черно-белые, контрастные; желательно созданные непосредственно в Microsoft Word: основные линии (графики и т.п.) – толщина 1,25 пт; вспомогательные линии (оси координат и т.п.) – толщина 0,75 пт; второстепенные вспомогательные линии (сноски, штриховки и т.п.) – толщина 0,5 пт) помещаются в текст после первой ссылки в виде переносимых объектов и раздельно нумеруются, при наличии более одного рисунка (таблицы), арабскими цифрами. Рисунок дополняется подрисуночной центрированной подписью под иллюстрацией, как показано на рис. 1. Все элементы рисунка, включая надписи и подрисуночную подпись, должны быть сгруппированы. Рисунок, созданный в другом редакторе, должен иметь расширение jpg (допускается расширение gif). Обтекание рисунка – с верху и снизу (допускается использовать обтекание вокруг рамки рисунка, если ширина рамки не превышает половины ширины страницы).
Рис. 2. Двухзвенная система
Таблица дополняется надписью, которая располагается справа над таблицей. Табличный заголовок располагается над таблицей по центру, что иллюстрируется табл.1. Выравнивание таблицы – слева (по краю основного текста) (допускается выравнивание по центру). Обтекание – нет (допускается использовать обтекание вокруг рамки таблицы, если ширина рамки не превышает половины ширины страницы). Таблица 1 Результаты численных расчетов
Если рисунков несколько, то в ссылке слово «рисунок» сокращается: «на рис. 1…», «см. рис. 2», «на рис. 4». При наличии нескольких таблиц, над каждой из них справа после слова «Таблица» указывается номер. Ссылка аналогична ссылке на рисунок. Через одну пустую строку после основного текста контрольной работы печатается список использованной литературы. Список литературы начинается с набранных полужирным шрифтом слов “Список литературы”, вслед за которыми ставится двоеточие. Сам список литературы набирается сплошным текстом с выделением фамилий и инициалов авторов курсивом. Не допускать отрыв номера позиции в списке литературы и инициалов от фамилии автора. Если авторов больше трех, то после фамилий первых двух авторов указывается «и др.». Образец: Список литературы: 1. Иванов Л. И., Смирнов В. Т. и др. Факторный анализ в социальных исследованиях. М., 1996. 352 с. 2. Петров В. С. Применение методов кластерного анализа при обработке данных экспертного опроса// Автоматика. 1995. № 3. С. 15 — 18. 3. Тишков В. Т. Кластерный анализ в социальных исследованиях// Вестн. Харьк. политехн. ин–та. 1990. № 260: Техн. кибернетика и ее прил. Вып. 10. С. 5 — 7. 4. Иванов Л. В., Петров В. С. Применение методов статистического анализа при обработке данных опроса населения// Статистический анализ социально-экономических данных/ Под ред. Р. В. Сидорова. - К., 1997. С. 57 — 65. После списка литературы через одну пустую строку указывается дата отправления контрольной работы и электронный адрес получателя с фамилией и инициалами преподавателя. Затем через одну пустую строку указывается фамилия и инициалы отправителя, а также обычный почтовый адрес и электронный адрес (при наличии) для связи с отправителем. Образец:
Контрольная работа отправлена на кафедру высшей математики ХНУГХ доц. Якунину А.В. 16.12.2013 г. по адресу: E-mail: vm_kolosov@ksame.kharkov.ua
Обратный адрес: Сидоров И.К., 52302 г. Донецк, ул. Артема, 26, кв.43 E-mail: sidorov_iv@kpi.donetsk.ua
Елементи лінійної алгебри Приклад.
Знайти матрицю 2А + 3В. Розв’язання.
У подальшому ми визначимо також і операцію множення матриць.
Визначник матриці Якщо Кожній квадратній матриці ставиться у відповідність число, яке називається її визначником. Визначник позначається так
Число n називається порядком квадратної матриці та її визначника. Визначники другого та третього порядку Визначник другого порядку обчислюється за формулою
Приклад. Обчислити визначник Розв’язання. Визначник третього порядку обчислюється розкладанням по елементам першого рядка, тобто за такою формулою:
Приклад. Обчислити визначник Розв’язання.
Елемента визначника Мінором Алгебраїчне доповнення
Наприклад, для визначника третього порядку
Тоді для визначника |A| має місце формула
Визначник дорівнює сумі добутків елементів і-го рядка на їх алгебраїчні доповнення. Останнє формулювання застосовується також для визначників більш високих порядків.
Добуток матриць Розглянемо дві матриці, одну розмірності
де m, n і p довільні натуральні числа. Оскільки кількість стовпців матриці А дорівнює кількості рядків матриці В, ми можемо установити взаємо однозначну відповідність між елементами будь-якого рядка матриці А та будь-якого стовпця матриці В. Для і-того рядка матриці А та j-того стовпця матриці В елементу аi1 ми ставимо у відповідь b1j, елементу ai2 - b2j і т.д. Тепер ми можемо визначити добуток будь-якого рядка матриці А на будь-який стовпець матриці В як суму добутків відповідних елементів. Добутком матриці А розмірності сij = ai1b1j + ai2b2j +... + ainbnj. (*) Позначення Приклад. Знайти А В. Розв’язання: В цьому випадку m = 3, p = 3, n = 2. Нехай С = АВ. Тоді за формулою (*):
Отже, Зазначимо, що А·В, взагалі кажучи, не дорівнює В·А, навіть якщо обидва добутки мають зміст. Для визначників квадратних матриць однакового порядку має місце властивість
Обернена матриця
Матриця називається оберненою до матриці А та позначається А-1, якщо виконується умова Виявляється, що для будь-якої невиродженої матриці А порядку n, існує обернена, яка знаходиться за наступною формулою:
де Аij – алгебраїчне доповнення елемента аij.
Приклад. Розв’язання: Матриця невироджена, тому має обернену. Обчислимо алгебраїчні доповнення.
Тоді Перевіряючи, переконуємося, що
Мінори матриці Мінором порядку k Ранг матриці Рангом матриці називається найбільший порядок відмінного від нуля мінора цієї матриці. Ранг матриці позначається rgA.
Приклад.
Розв’язання: rgА = 1, оскільки усі мінори другого порядку дорівнюють 0, але є ненульові мінори першого порядку. rgВ = 2, бо єдиний мінор третього порядку -
Системи m лінійних алгебраїчних рівнянь зі сталими коефіцієнтами і n невідомими Розглянемо систему m лінійних рівняньз n невідомими х1, х2,..., хп. Вона має вигляд:
де aij (i = 1, 2, …., m; j = 1, 2, …., n) – відомі коефіцієнти, а b1, b2, …., bm – відомі вільні члени. Система лінійних рівнянь називається сумісною, якщо вона має принаймні один розв’язок, та несумісною, якщо не має розв’язків. Введемо позначення
Тоді систему рівнянь можна записати в матричній формі
Якщо матрицю системи А доповнити матрицею-стовпцем В, отримаємо розширену матрицю системи С:
Теорема Кронекера-Капеллі Для сумісності системи лінійних рівнянь необхідно і достатньо, щоб ранг матриці А системи дорівнював рангу розширеної матриці С.
Розв’язання системи Якщо система лінійних рівнянь має рівнянь стільки скільки невідомих і матриця А невироджена, то система має єдиний розв’язок:
де А-1 – матриця обернена до матриці А. Розв’язок такої системи можна знайти також за правилом Крамера:
де
Приклад. Розв’язати наступну систему лінійних рівнянь матричним методом та за правилом Крамера:
Розв’язання. Спочатку шукаємо розв’язок матричним методом. Тут тоді
Обчислюємо усі алгебраїчні доповнення (приклад надано вище) та за їх допомогою записуємо обернену матрицю. Вона буде мати такий вигляд:
тоді
Отже: х1 = 0, х2 = х3 = 1. Використовуючи формули Крамера отримуємо:
Відповіді, отримані двома методами, співпали.
Елементи векторної алгебри Координатних ортів Ортом називається вектор одиничної довжини. Координатний орт Орти
де ах, ay, az – деякі числа, які називаються координатами вектора
Дії з векторами дуже просто записуються у координатній формі. Нехай: тоді
Довжина вектора Нехай Кут між двома векторами
Кут між двома векторами
Приклад. Задані вершини А(0, -1, 2), В(3, -1, 1), С(5, 0, 3) трикутника. Знайти довжини сторін АВ і АС та кут Розв’язання. Спочатку запишемо вектори
Тоді
Значення квадратного кореня та кута А знаходимо за допомогою калькулятора або у таблицях. Двох векторів
Два вектори паралельні, якщо їхні однойменні координати пропорційні: Два вектори перпендикулярні, тоді й тільки тоді, коли
Площа трикутника Площа трикутника, побудованого на векторах
Приклад. Знайти площу трикутника з вершинами А(2, 1, -2), В(5, 3, 1), С(3, 4, 2). Розв’язання. Виділимо два вектори:
одиниць квадратних.
Об’єм піраміди Модуль мішаного добутку дорівнює об’єму паралелепіпеда, побудованого на векторах-співмножниках, як на ребрах. Якщо відомі координати вершин S, A, B, C – трикутної піраміди, то її об’єм можна обчислити за формулою
Приклад. Задані координати вершин трикутної піраміди: S(1, 1, -2), A(5, 2, 1), B(3, 5, 1), C(-3, -2, -6). Знайти її об’єм. Розв’язання.
Елементи аналітичної геометрії Відстань між двома точками Нагадаємо, що для двох точок М1(х1, у1) та М2(х2, у2) площини відстань d між ними знаходиться за формулою
а відстань між точками М1(х1, у1, z1) і М2(х2, у2, z2) простору буде:
Пряма лінія на площині Наводимо основні види рівнянь прямої на площині:
1. Рівняння прямої з кутовим коефіцієнтом
Розглянемо деякі окремі випадки цього рівняння: а) б) в) Якщо пряма перпендикулярна до осі
2. Рівняння прямої, що проходить через дану точку у даному напрямку. Нехай відомий кутовий коефіцієнт прямої
3. Рівняння прямої, що проходить через дві дані точки. Якщо
Приклад. Скласти рівняння прямої, що проходить через точки Розв’язання. Тут
4. Загальне рівняння прямої. Рівняння кожної прямої можна записати у вигляді
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.130.31 (0.276 с.) |

 косой черты
косой черты  или двоеточия
или двоеточия  ; 2) вместо символа суммы
; 2) вместо символа суммы  символа
символа  ; 3) вместо символов интеграла
; 3) вместо символов интеграла  ,
,  ,
,  символов
символов  ,
,  ,
,  и т.п.
и т.п.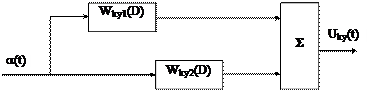
 ,
, 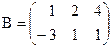 .
.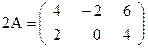 ,
,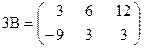
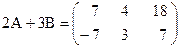 .
.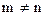 , матриця називається прямокутною, якщо
, матриця називається прямокутною, якщо 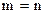 – квадратною.
– квадратною. .
.

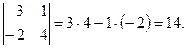
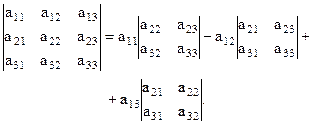
 .
.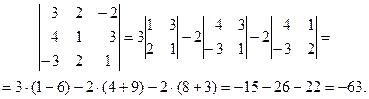
 елемента визначника n–го порядку |A| називається визначник порядку n-1, який ми одержимо з визначника |A|, якщо закреслимо i-й рядок та j-й стовпець.
елемента визначника n–го порядку |A| називається визначник порядку n-1, який ми одержимо з визначника |A|, якщо закреслимо i-й рядок та j-й стовпець.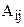 елемента aij визначається формулою
елемента aij визначається формулою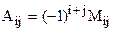
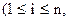

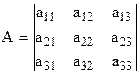 ми маємо:
ми маємо: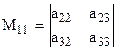 ,
, 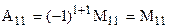 ;
;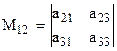 ,
, 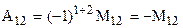 ;
;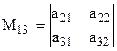 ,
, 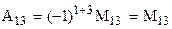 .
.
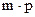 , другу -
, другу - 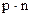 :
: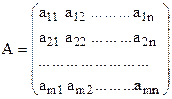 ;
; 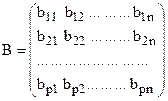 ,
,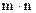 , якщо кожний елемент сij
, якщо кожний елемент сij 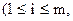
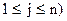 дорівнює добутку і-го рядка матриці А на j-й стовпець матриці В:
дорівнює добутку і-го рядка матриці А на j-й стовпець матриці В: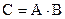 .
. ,
, 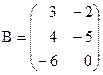 .
.
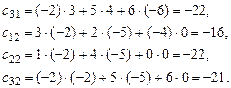
 .
. , тобто визначник добутку матриць дорівнює добутку визначників матриць співмножників. Якщо |A| = 0, матриця А називається виродженою. Елементи а11, а22,..., аnn утворюють головну діагональ матриці А порядку n. Матриця, головна діагональ якої складається з одиниць, а інші елементи – нулі, називається одиничною та позначається літерою Е. Ця матриця виконує функцію одиниці при множенні матриць:
, тобто визначник добутку матриць дорівнює добутку визначників матриць співмножників. Якщо |A| = 0, матриця А називається виродженою. Елементи а11, а22,..., аnn утворюють головну діагональ матриці А порядку n. Матриця, головна діагональ якої складається з одиниць, а інші елементи – нулі, називається одиничною та позначається літерою Е. Ця матриця виконує функцію одиниці при множенні матриць: , для усіх А..
, для усіх А..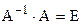 (або еквівалентно
(або еквівалентно 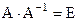 ).
). ,
,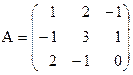 . Знайти А-1.
. Знайти А-1. .
. ,
, 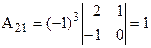 ,
,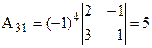 ,
, 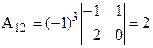 ,
,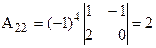 ,
,  ,
,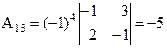 ,
, 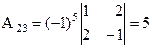 ,
, .
. .
. матриці А називається будь-який визначник, який складається з деяких k рядків та k стовпців матриці А. Мінором першого порядку називається будь-який елемент матриці А.
матриці А називається будь-який визначник, який складається з деяких k рядків та k стовпців матриці А. Мінором першого порядку називається будь-який елемент матриці А.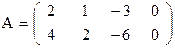 ,
, 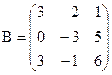
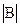 , як легко перевірити, дорівнює нулю, а мінор другого порядку
, як легко перевірити, дорівнює нулю, а мінор другого порядку .
.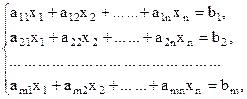
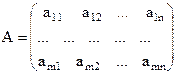 ,
,  ,
,  .
. .
.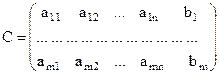 .
.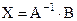 ,
,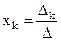 ; (k = 1, 2, …, n),
; (k = 1, 2, …, n),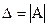 , а
, а 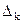 - визначник, який отримується з визначника Δ заміною в ньому k-го стовпця стовпцем вільних членів В.
- визначник, який отримується з визначника Δ заміною в ньому k-го стовпця стовпцем вільних членів В.
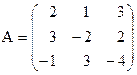 і
і 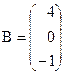 ,
, .
.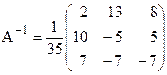
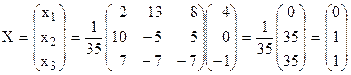 .
.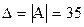 ;
; 
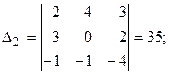
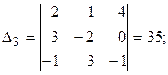
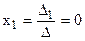 ;
; 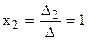 ;
;  .
.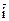 - одиничний вектор, спрямований вздовж напрямку осі х,
- одиничний вектор, спрямований вздовж напрямку осі х,  - вздовж осі у,
- вздовж осі у,  - вздовж осі z.
- вздовж осі z.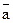 у цьому просторі єдиним чином подається у вигляді:
у цьому просторі єдиним чином подається у вигляді: ,
, .
. ;
; ;
; ;
; ;
;  .
. .
.  знаходиться з співвідношення:
знаходиться з співвідношення:
 між ними з точністю до
між ними з точністю до  .
. і
і  :
:
 .
. .
. .
.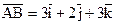 ;
; 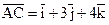 ;
;
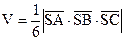 .
.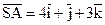 ;
;  ;
;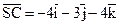 . Тоді
. Тоді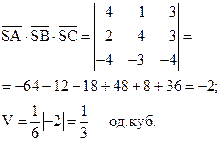
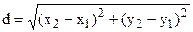 ,
, .
. , де
, де  - кутовий коефіцієнт прямої, тобто тангенс кута, який пряма утворює з додатним напрямком осі
- кутовий коефіцієнт прямої, тобто тангенс кута, який пряма утворює з додатним напрямком осі 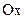 , причому цей кут відраховується від осі
, причому цей кут відраховується від осі  - ордината точки перетину прямої з віссю
- ордината точки перетину прямої з віссю  .
. - пряма проходить через початок координат;
- пряма проходить через початок координат;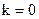 - пряма паралельна осі
- пряма паралельна осі 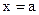 , де а – абсциса точки перетину прямої з віссю
, де а – абсциса точки перетину прямої з віссю 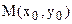 , яка належить прямій. Тоді її рівняння має вигляд:
, яка належить прямій. Тоді її рівняння має вигляд: .
. і
і  - точки, які належать прямій, тоді її рівняння
- точки, які належать прямій, тоді її рівняння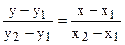 .
.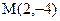 і
і 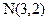 .
. ,
,  ,
,  ,
,  , тоді
, тоді ;
; 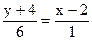 ;
; ;
;  .
.


