
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектори. Означення, операції з векторамиСодержание книги
Поиск на нашем сайте
Вектором називається спрямований відрізок. Позначається Два вектора називаються рівними, якщо виконуються 3 умови: 1. Довжини векторів співпадають. 2. Вектори лежать на одній прямій або на паралельних прямих (такі вектори називаються колінеарними). 3. Вектори спрямовані в один бік. Сума векторів визначається за правилом паралелограма. Нехай λ – число, 1. | λ 2. Вектори λ 3. Якщо λ > 0, вектори λ Вектор (
Скалярний добуток двох векторів Для векторів
де Відмітимо: а) скалярний добуток двох векторів дорівнює 0, якщо вектори перпендикулярні або один з множників – нульовий вектор; б) в) Дії з векторами, розкладеними за базисом Координатних ортів Ортом називається вектор одиничної довжини. Координатний орт Орти
де ах, ay, az – деякі числа, які називаються координатами вектора
Дії з векторами дуже просто записуються у координатній формі. Нехай: тоді
Довжина вектора Нехай Кут між двома векторами
Кут між двома векторами
Приклад. Задані вершини А(0, -1, 2), В(3, -1, 1), С(5, 0, 3) трикутника. Знайти довжини сторін АВ і АС та кут Розв’язання. Спочатку запишемо вектори
Тоді
Значення квадратного кореня та кута А знаходимо за допомогою калькулятора або у таблицях. Умови паралельності та перпендикулярності Двох векторів
Два вектори паралельні, якщо їхні однойменні координати пропорційні: Два вектори перпендикулярні, тоді й тільки тоді, коли
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.149 (0.008 с.) |

 . А називається початком, В – кінцем. Довжиною вектора
. А називається початком, В – кінцем. Довжиною вектора 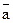 (|
(|  .
. |
|  1)
1)  та називається вектором протилежним до вектора
та називається вектором протилежним до вектора  .
. їх скалярним добутком
їх скалярним добутком  називається число, яке дорівнює добутку довжин цих векторів, помноженому на косинус кута між ними:
називається число, яке дорівнює добутку довжин цих векторів, помноженому на косинус кута між ними: ,
, - кут між векторами
- кут між векторами  =
=  . Зміна місць співмножників на скалярний добуток не впливає.
. Зміна місць співмножників на скалярний добуток не впливає. .
.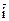 - одиничний вектор, спрямований вздовж напрямку осі х,
- одиничний вектор, спрямований вздовж напрямку осі х,  - вздовж осі у,
- вздовж осі у,  - вздовж осі z.
- вздовж осі z. ,
, .
. ;
; ;
; ;
; ;
;  .
. .
. 
 між ними з точністю до
між ними з точністю до  .
. :
:
 .
. .
.


