
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напрямні кути та напрямні косинуси вектора
Напрямні кути Напрямні косинуси вектора – це косинуси його напрямних кутів. Нехай
Напрямні косинуси зв’язані співвідношенням
Векторний добуток двох векторів Векторний добуток 1) 2) довжина вектора 3) вектор Векторний добуток дорівнює Відмітимо, що векторний добуток не комутативний:
Якщо вектори задані своїми координатами:
то має місце формула:
Площа трикутника Площа трикутника, побудованого на векторах
Приклад. Знайти площу трикутника з вершинами А(2, 1, -2), В(5, 3, 1), С(3, 4, 2). Розв’язання. Виділимо два вектори:
одиниць квадратних.
Мішаний добуток трьох векторів. Мішаним добутком трьох векторів
Об’єм піраміди Модуль мішаного добутку дорівнює об’єму паралелепіпеда, побудованого на векторах-співмножниках, як на ребрах. Якщо відомі координати вершин S, A, B, C – трикутної піраміди, то її об’єм можна обчислити за формулою
Приклад. Задані координати вершин трикутної піраміди: S(1, 1, -2), A(5, 2, 1), B(3, 5, 1), C(-3, -2, -6). Знайти її об’єм. Розв’язання.
Елементи аналітичної геометрії Відстань між двома точками Нагадаємо, що для двох точок М1(х1, у1) та М2(х2, у2) площини відстань d між ними знаходиться за формулою
а відстань між точками М1(х1, у1, z1) і М2(х2, у2, z2) простору буде:
Поділ відрізка у даному відношенні Нехай відомі координати кінців відрізка АВ: А(х1, у1, z1), В(х2, у2, z2) і відомо, що точка С ділить відрізок АВ у відношенні λ, тобто АС: СВ = λ. Тоді координати точки С(х, у, z) обчислюються за формулами
Якщо С – середина відрізка АВ, то λ = 1 і ми отримуємо
Приклад. Задані точки А(1, 1, 1), В(7, 4, 4). Знайти на відрізку АВ точку С(х, у, z), яка в два рази ближче до А, ніж до В. Розв’язання. Шукана точка С ділить відрізок АВ у відношенні λ = 1/2. Тоді її координати будуть:
Для двомірного простору координата z відсутня.
Пряма лінія на площині Наводимо основні види рівнянь прямої на площині:
1. Рівняння прямої з кутовим коефіцієнтом
Розглянемо деякі окремі випадки цього рівняння: а) б) в) Якщо пряма перпендикулярна до осі
2. Рівняння прямої, що проходить через дану точку у даному напрямку. Нехай відомий кутовий коефіцієнт прямої
3. Рівняння прямої, що проходить через дві дані точки. Якщо
Приклад. Скласти рівняння прямої, що проходить через точки Розв’язання. Тут
4. Загальне рівняння прямої. Рівняння кожної прямої можна записати у вигляді
Навпаки, кожному рівнянню першого ступеня з двома змінними відповідає деяка пряма. Якщо задане рівняння прямої
Приклад. Знайти відстань від точки М(1, 2) до прямої 3х – 4у + 10 = 0. Розв’язання.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 822; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.235 (0.02 с.) |
 ,
, 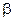 ,
, 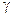 - це кути, які вектор утворює з додатними напрямками координатних осей (з координатними ортами).
- це кути, які вектор утворює з додатними напрямками координатних осей (з координатними ортами). , тоді:
, тоді: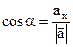 ;
; 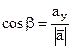 ;
;  .
.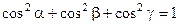 .
.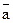 і
і  - це вектор
- це вектор  , що задовольняє умовам:
, що задовольняє умовам: , якщо вектори паралельні або один з векторів нульовий.
, якщо вектори паралельні або один з векторів нульовий. .
. .
.  .
.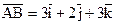 ;
; 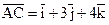 ;
;
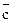 називається число, яке дорівнює скалярному добутку вектора
називається число, яке дорівнює скалярному добутку вектора 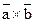 на вектор
на вектор  . Якщо вектори задані своїми координатами, він обчислюється за формулою:
. Якщо вектори задані своїми координатами, він обчислюється за формулою: .
.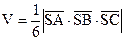 .
.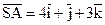 ;
;  ;
;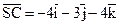 . Тоді
. Тоді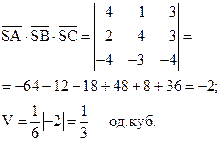
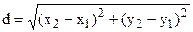 ,
, .
. ;
; 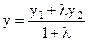 ;
;  .
.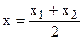 ;
; 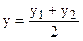 ;
; 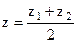 .
.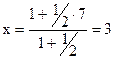 ;
;  ;
; 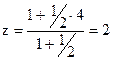 .
. , де
, де  - кутовий коефіцієнт прямої, тобто тангенс кута, який пряма утворює з додатним напрямком осі
- кутовий коефіцієнт прямої, тобто тангенс кута, який пряма утворює з додатним напрямком осі 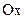 , причому цей кут відраховується від осі
, причому цей кут відраховується від осі  - ордината точки перетину прямої з віссю
- ордината точки перетину прямої з віссю  .
. - пряма проходить через початок координат;
- пряма проходить через початок координат;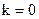 - пряма паралельна осі
- пряма паралельна осі 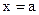 , де а – абсциса точки перетину прямої з віссю
, де а – абсциса точки перетину прямої з віссю 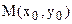 , яка належить прямій. Тоді її рівняння має вигляд:
, яка належить прямій. Тоді її рівняння має вигляд: .
. і
і  - точки, які належать прямій, тоді її рівняння
- точки, які належать прямій, тоді її рівняння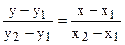 .
.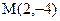 і
і 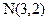 .
. ,
,  ,
,  ,
,  , тоді
, тоді ;
; 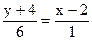 ;
; ;
;  .
. .
. .
.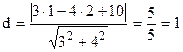 .
.


