
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференційні рівняння другого порядку
Для визначення цих сталих використовуємо початкові умови, тобто відомі значення шуканої функції у та її похідної Нижче розглянемо два види найпростіших диференційних рівнянь другого порядку, які розв’язуються методом зниження порядку. 1. У рівнянні відсутня шукана функція, тобто рівняння має вигляд Порядок рівняння знижується шляхом заміни Приклад. Розв'язати рівняння Розв'язання. Нехай
Тоді
2. У рівнянні відсутня незалежна змінна, тобто воно має вигляд Порядок рівняння знижується шляхом заміни Для Приклад. Розв'язати рівняння Розв'язання. Нехай Відокремивши змінні, одержимо Після його інтегрування маємо: Або Відокремивши змінні та проінтегрувавши його, одержимо загальний розв'язок вихідного рівняння
Лінійні диференційні рівняння другого порядку Зі сталими коефіцієнтами Рівняння вигляду Якщо Наприклад, рівняння Однорідні. Для розв'язання однорідного рівняння 1. Якщо характеристичне рівняння має два дійсні корені
Приклад. Знайти розв'язок рівняння Розв'язання. Характеристичне рівняння
2. Якщо характеристичне рівняння має однакові дійсні корені
Приклад. Знайти розв'язок рівняння Розв'язання. Характеристичне рівняння
3. Якщо дискримінант D характеристичного рівняння від'ємний, воно має комплексні корені вигляду
Приклад. Знайти розв'язок рівняння Розв'язання. Дискримінант характеристичного рівняння
Неоднорідні. Загальний розв'язок лінійного неоднорідного диференційного рівняння Розглянемо деякі функції 1. Приклад. Знайти розв'язок рівняння Розв'язання. Характеристичне рівняння
Отже, Підставляємо Прирівнюючи коефіцієнти при однакових степенях х у лівій та правій частинах рівняння, одержуємо систему відносно невідомих А та В:
Маємочастинний розв'язок 2. Приклад. Знайти загальний розв'язок рівняння Розв'язання. Корені характеристичного рівняння
Знаходимо
Підставляємо
Загальний розв'язок рівняння: 3. Приклад. Знайти загальний розв'язок рівняння Розв'язання. Корені характеристичного рівняння Тоді Підставляємо
Прирівнюючи коефіцієнти при sin2x та cos2x, одержуємо систему:
Отже, а
Задача Коши Знаходження частинного розв'язку диференційного рівняння, який задовольняє початковим умовам, називається задачею Коши.
Приклад. Розв'язати рівняння Розв'язання. Спочатку знаходимо загальний розв'язок рівняння:
Для знаходження
Далі знаходимо Використовуємо умову
Одержуємо систему
Частинний розв'язок диференційного рівняння, який задовольняє початковим умовам, має вигляд:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.248.208 (0.025 с.) |
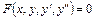 - загальний вигляд диференційного рівняння другого порядку. Загальний розв'язок такого рівняння має вигляд
- загальний вигляд диференційного рівняння другого порядку. Загальний розв'язок такого рівняння має вигляд 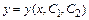 , тобто залежить від двох довільних сталих.
, тобто залежить від двох довільних сталих.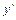 при даному значенні аргументу
при даному значенні аргументу 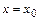 .
.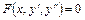 .
.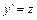 ,
,  , де z =z(x) – допоміжна шукана функція.
, де z =z(x) – допоміжна шукана функція.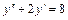 .
.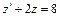 . Відокремивши змінні, отримуємо
. Відокремивши змінні, отримуємо ;
; 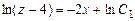 .
. або
або 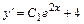 і, нарешті,
і, нарешті,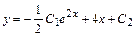 - загальний розв'язок рівняння.
- загальний розв'язок рівняння. .
.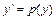 - нова шукана функція від незалежної змінної у, яка в свою чергу є функція від x.
- нова шукана функція від незалежної змінної у, яка в свою чергу є функція від x.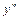 отримуємо співвідношення
отримуємо співвідношення 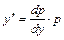 .
. .
. ;
;  .
. .
. .
. , звідки
, звідки  ,але
,але  .
. .
. називається диференційним рівнянням другого порядку зі сталими коефіцієнтами, якщо р та q – відомі числа, а
називається диференційним рівнянням другого порядку зі сталими коефіцієнтами, якщо р та q – відомі числа, а  - відома функція.
- відома функція. є однорідним, а рівняння
є однорідним, а рівняння 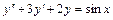 є неоднорідним.
є неоднорідним. виписуємо так зване характеристичне рівняння
виписуємо так зване характеристичне рівняння 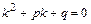 .
.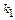 і
і  (
(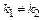 ), тоді загальний розв'язок однорідного рівняння має вигляд:
), тоді загальний розв'язок однорідного рівняння має вигляд: .
.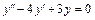 .
.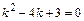 має два дійсні корені:
має два дійсні корені: 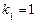 ,
, 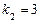 . Отже
. Отже .
.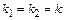 , тоді загальний розв'язок однорідного рівняння має вигляд:
, тоді загальний розв'язок однорідного рівняння має вигляд: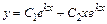 .
.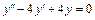 .
.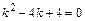 має однакові дійсні корені:
має однакові дійсні корені: 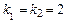 . Отже
. Отже .
. , (тут
, (тут  ,
, 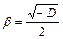 ,
, 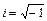 - називають уявною одиницею),тоді загальний розв'язок однорідного рівняння має вигляд:
- називають уявною одиницею),тоді загальний розв'язок однорідного рівняння має вигляд: .
. .
. D =16-52=-36. Тут
D =16-52=-36. Тут 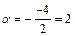 ,
, 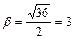 . Отже
. Отже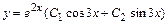 .
.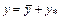 , де
, де 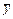 - загальний розв'язок однорідного рівняння (див. попередній пункт), а
- загальний розв'язок однорідного рівняння (див. попередній пункт), а  - який-небудь частинний розв'язок початкового рівняння. Вигляд
- який-небудь частинний розв'язок початкового рівняння. Вигляд 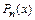 . Тоді
. Тоді 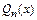 , якщо
, якщо 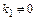 ,
,  . Якщо один з коренів характеристичного рівняння дорівнює нулю, то
. Якщо один з коренів характеристичного рівняння дорівнює нулю, то 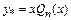 .
.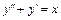 .
.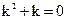 має два дійсні корені:
має два дійсні корені:  ,
,  . Отже,
. Отже,  .
. , де А і В – невідомі, оскільки один з коренів характеристичного рівняння дорівнює нулю, а права частина – многочлен першого степеня.
, де А і В – невідомі, оскільки один з коренів характеристичного рівняння дорівнює нулю, а права частина – многочлен першого степеня.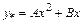 . Тоді
. Тоді 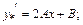
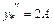 .
. та
та  у рівняння:
у рівняння: 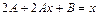 .
.
 ,
,  .
. і загальний розв'язок початкового рівняння:
і загальний розв'язок початкового рівняння:  .
. . Тоді
. Тоді  , де r – число коренів характеристичного рівняння, які дорівнюють m.
, де r – число коренів характеристичного рівняння, які дорівнюють m. .
. ,
, 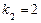 .
. ;
;  (тут
(тут 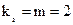 ,тому r =1).
,тому r =1).
 .
.
 . Звідки А =1,
. Звідки А =1, 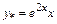 .
.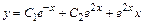 .
. . Тоді
. Тоді 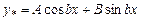 , якщо корені характеристичного рівняння не дорівнюють
, якщо корені характеристичного рівняння не дорівнюють 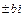 , і
, і  - в протилежному разі.
- в протилежному разі. .
.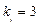 ,
, 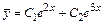 ;
; 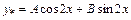 .
.
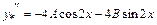 .
.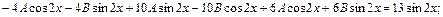
 .
. Відкіля
Відкіля 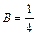 ,
, 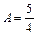 .
. - частинний розв'язок,
- частинний розв'язок,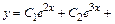
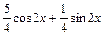 - загальний розв'язок початкового рівняння.
- загальний розв'язок початкового рівняння. , якщо у (0)=0,
, якщо у (0)=0,  .
. ;
;  . Тоді
. Тоді 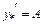 ,
,  . Отже,
. Отже,  . Тоді
. Тоді 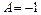 ,
, 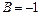 . Загальний розв'язок рівняння
. Загальний розв'язок рівняння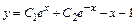 .
.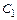 і
і 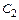 використовуємо спочатку умову у (0)=0:
використовуємо спочатку умову у (0)=0: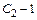 =0.
=0.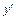 :
:  .
.
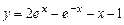 . Тобто задачу Коши розв’язано.
. Тобто задачу Коши розв’язано.


