
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения с разделяющимися переменнымиСтр 1 из 7Следующая ⇒
Кафедра высшей математики
Рекомендовано ученым советом инженерно-экономического факультета
Обыкновенные ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Методические указания и задания для контрольных работ для студентов факультета дополнительного профессионального образования
Ярославль УДК 517(07)
МУ 33-08. Обыкновенные дифференциальные уравнения: Метод. указания и задания для контрольных работ для студентов факультета дополнительного профессионального образования / Сост.: В.А. Журавлева, Т.П. Чуйко, Л.А. Сидорова. – Ярославль: Изд-во ЯГТУ, 2008. – 48 с.
Содержат краткие теоретические сведения по разделу «Дифференциальные уравнения», подробно разобранные типовые задачи, а также 30 вариантов контрольных заданий. Предназначены для студентов 2 курса всех направлений и специальностей факультета дополнительного профессионального образования. Могут быть полезны при подготовке контрольных работ и выполнении домашних заданий.
Илл. 2. Библиогр. 5.
Рецензенты: кафедра высшей математики Ярославского государственного технического университета; Н.И. Иванова, канд. физ.-мат. наук, доцент кафедры статистики и математики ЯФ МЭСИ.
_______________________________________________________________ План 2008
Редактор В.Б. Доронина
Подписано в печать 27.04.08. Формат 60х84 1/16. Бумага белая. Печать ризограф. Усл. печ. л. 2,79. Уч.-изд. л. 2,74. Тираж 400. Заказ
Ярославский государственный технический университет 150023, Ярославль, Московский пр., 88
Типография Ярославского государственного технического университета 150000, Ярославль, ул. Советская, 14а ã Ярославский государственный технический университет, 2008
Дифференциальные уравнения Первого порядка Основные понятия Сведения из теории Дифференциальным уравнением называется уравнение, которое содержит независимые переменные, неизвестные функции, зависящие от этих переменных, а также производные неизвестных функций или их дифференциалы. Если функции, входящие в дифференциальное уравнение, зависят от одной независимой переменной, уравнение называется обыкновенным дифференциальным уравнением. Наивысший порядок производной от искомой функции, входящей в уравнение, называется порядком этого уравнения.
Уравнение
называется дифференциальным уравнением первого порядка, где Если из уравнения можно выразить
Решением дифференциального уравнения или называется функция Рассмотрим простейшее дифференциальное уравнение первого порядка
Решением этого уравнения будет первообразная функции
где Совокупность всех его решений называется общим решением дифференциального уравнения. В явном виде общее решение можно записать В неявном виде общее решение записывается
и называется общим интегралом уравнения. При решении реальных задач бывает нужно не общее, а частное решение дифференциального уравнения, удовлетворяющее некоторым дополнительным условиям, которые называются начальными условиями. Задача о нахождении частного решения дифференциального уравнения при заданных начальных условиях называется задачей Коши и формулируется следующим образом: Найти решение дифференциального уравнения где Примеры решения задач 1. Найти частное решение уравнения ◄ 1) Это простейшее дифференциальное уравнение вида. Его решение получим интегрированием
2) Для нахождения частного решения подставим в общее решение значения Сведения из теории Если дифференциальное уравнение имеет вид
то ононазывается дифференциальным уравнением с разделяющимися переменными. Для его решения представим Примеры решения задач 1. Найти общее решение уравнения ◄ Это уравнение можно представить в виде
2. Найти решение уравнения ◄ Надо решить задачу Коши при начальных данных
Для нахождения частного решения надо найти C. Подставим в последнее равенство
Вернемся к общему решению. Подставим в него 3. Решить уравнение ◄ Разделяем переменные:
Однородные уравнения Сведения из теории Если дифференциальное уравнение записано в нормальном виде и в его правой части присутствует выражение, содержащее искомую функцию в виде отношения
Оно сводится заменой переменной переменными, где
– уравнение с разделяющимися переменными. Разделим переменные Вычислив интегралы, получим общий интеграл и вернемся к старой функции, заменив
Примеры решения задач 1. Решить уравнение ◄ Разделим обе части уравнения на x:
В правую часть уравнения y и x входят только в виде отношения
Вернемся к y: 2. Найти решение дифференциального уравнения ◄ Разделим равенство почленно на x:
В правую часть уравнения y и x входят только в виде отношения
Вернемся к y:
Уравнение Бернулли Сведения из теории Уравнение вида
называется линейным уравнением первого порядка. Если
Уравнение вида
называется уравнением Бернулли. Уравнения и могут быть решены методом Бернулли, который заключается в нахождении решения
Функцию Вспомним, что
При таком подборе функции Примеры решения задач 1. Решить задачу Коши: ◄ Уравнение имеет вид, то есть это линейное уравнение, где
Функцию Решим сначала уравнение 2. Решить уравнение
◄ Приведем уравнение к виду:
Решаем первое уравнение с разделяющимися переменными
Пусть
По свойствам логарифмов 1) Из последнего равенства получим
Вернемся к решению уравнения Дифференциальные уравнения Высших порядков Основные понятия
Сведения из теории Общий вид дифференциального уравнения n -го порядка:
где x – независимая переменная, y – искомая функция, зависящая от x. В общем случае функция
и называется общим интегралом или общим решением уравнения. Если придать каждой произвольной постоянной Чтобы из общего решения выделить одно частное решение, необходимо задать начальные условия:
Рассмотрим некоторые частные случаи решения уравнения, где n больше единицы.
2.2. Простейшее дифференциальное уравнение n -го порядка Сведения из теории Дифференциальное уравнение вида
решается n- кратным интегрированием:
…………..
Примеры решения задач 1. Решить уравнение ◄
2. Решить уравнение ◄ Приведем уравнение к виду.
Уравнение второго порядка, Сведения из теории Рассмотрим дифференциальное уравнение второго порядка
Решить это уравнение можно понижением порядка. Для этого введем замену Примеры решения задач 1. Решить задачу Коши ◄ Так как уравнение не содержит зависимой переменной y, то для понижения порядка введем замену
Разделим переменные
Для нахождения
Уравнение второго порядка, не содержащее явно независимой переменной x Сведения из теории
– дифференциальное уравнение второго порядка этого типа. Понижаем порядок с помощью замены
Примеры решения задач
1. Решить дифференциальное уравнение ◄ Уравнение не содержит явно независимой переменной
Таким образом, Проинтегрируем уравнение:
Комплексные числа Сведения из теории
Действительные числа a содержатся в классе комплексных чисел в качестве пар Мнимой единицей называется число Два комплексных числа Примеры решения задач
Вспомним формулы для решения квадратного уравнения Если
Если Если
1. Решить квадратное уравнение ◄ Вычислим дискриминант для данного уравнения: 2. Решить квадратное уравнение ◄
для которых
Основные понятия Сведения из теории Общий вид линейного однородного уравнения n -го порядка
Теорема. Если Для нахождения общего решения уравнения как линейной комбинации частных решений с постоянными коэффициентами
Решив его, получим n корней: Второго порядка Сведения из теории Уравнение вида
называется линейным однородным уравнением второго порядка. Коэффициенты Линейные однородные уравнения обладают следующим свойством: линейная комбинация решений линейного однородного уравнения также является решением этого уравнения. Если Система линейно независимых частных решений Дифференциальному уравнению второго порядка можно поставить в соответствие алгебраическое уравнение второй степени с теми же коэффициентами
Уравнение называется характеристическим уравнением для уравнения. Если при решении характеристического уравнения получим
где Если для уравнения
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.127.141 (0.19 с.) |
 ,
, – искомая функция независимой переменной x;
– искомая функция независимой переменной x;  – производная этой функции, а F – известная функция, зависящая от
– производная этой функции, а F – известная функция, зависящая от  .
. , то дифференциальное уравнение первого порядка будет иметь так называемый нормальный вид или вид, разрешенный относительно
, то дифференциальное уравнение первого порядка будет иметь так называемый нормальный вид или вид, разрешенный относительно 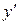 :
:
 .
. . Все множество решений задается формулой
. Все множество решений задается формулой ,
, – некоторая первообразная функции
– некоторая первообразная функции  , где C – произвольная постоянная.
, где C – произвольная постоянная.
 ,
,  (начальные условия),
(начальные условия),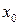 ,
,  – некоторые заданные числа.
– некоторые заданные числа. при заданных начальных условиях
при заданных начальных условиях 
 .
. . По таблице интегралов находим общее решение
. По таблице интегралов находим общее решение  .
. и
и  , получим
, получим  , отсюда
, отсюда  . Подставим найденное значение C в общее решение и получим
. Подставим найденное значение C в общее решение и получим  – частное решение, удовлетворяющее заданным начальным условиям. ►
– частное решение, удовлетворяющее заданным начальным условиям. ► ,
, . Разделим обе части уравнения на
. Разделим обе части уравнения на  и умножим на
и умножим на  :
:  . Проинтегрируем обе части равенства
. Проинтегрируем обе части равенства  . Отсюда
. Отсюда 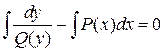 . Вычислив интегралы, получим общий интеграл уравнения
. Вычислив интегралы, получим общий интеграл уравнения  .
. .
. ;
;  . Таким образом, это уравнение является уравнением с разделяющимися переменными. Представляем
. Таким образом, это уравнение является уравнением с разделяющимися переменными. Представляем  :
:  . Интегрируем это равенство
. Интегрируем это равенство 
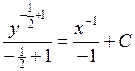

 – общий интеграл. Разрешим его относительно y:
– общий интеграл. Разрешим его относительно y:  ;
;  – общее решение. ►
– общее решение. ► , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
. . Разделим обе части уравнения на x:
. Разделим обе части уравнения на x: 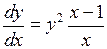 . Правая часть уравнения представлена в виде произведения двух функций
. Правая часть уравнения представлена в виде произведения двух функций  и
и  , следовательно, это уравнение с разделяющимися переменными. Разделим переменные
, следовательно, это уравнение с разделяющимися переменными. Разделим переменные  и проинтегрируем это равенство.
и проинтегрируем это равенство. .
. .
. и
и  :
: .
. . Получим частное решение
. Получим частное решение  . Выразим y:
. Выразим y:  – частное решение.►
– частное решение.► .
. ;
;  . Проинтегрируем последнее равенство
. Проинтегрируем последнее равенство  (Функция
(Функция  принимает все действительные значения, поэтому постоянную интегрирования можно представить в виде
принимает все действительные значения, поэтому постоянную интегрирования можно представить в виде  ). По свойствам логарифмов (
). По свойствам логарифмов ( ;
; 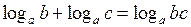 ) получим
) получим  отсюда
отсюда  – общее решение. ►
– общее решение. ► , то такое уравнение называется однородным
, то такое уравнение называется однородным .
. к уравнению с разделяющимися
к уравнению с разделяющимися – новая неизвестная функция. Выразим
– новая неизвестная функция. Выразим  . Так как
. Так как  , то приводится к виду
, то приводится к виду  ,
,  ;
;

 и проинтегрируем
и проинтегрируем  .
. .
. .
. , а затем - на
, а затем - на  :
: .
.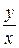 , то есть данное уравнение является однородным. Делаем замену
, то есть данное уравнение является однородным. Делаем замену  ,
,  . Для функции
. Для функции  получаем уравнение:
получаем уравнение:  или
или  . Приводя к общему знаменателю, получим уравнение с разделяющимися переменными:
. Приводя к общему знаменателю, получим уравнение с разделяющимися переменными:  . Заменим
. Заменим  на
на  и разделим переменные
и разделим переменные  .
. .
. - общее решение в неявном виде. ►
- общее решение в неявном виде. ► .
. . При внесении x под знак квадратного корня получим
. При внесении x под знак квадратного корня получим или
или 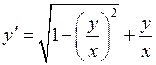 .
. или
или  , которое является уравнением с разделяющимися переменными. Заменим
, которое является уравнением с разделяющимися переменными. Заменим 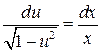 . Проинтегрируем
. Проинтегрируем  .
. - общее решение в неявном виде.►
- общее решение в неявном виде.►
 , то получаем линейное однородное уравнение
, то получаем линейное однородное уравнение .
. ,
,  .
. в виде произведения двух функций
в виде произведения двух функций  и
и  . Если
. Если  , то
, то  . Подставим решение в уравнение, которое обращается в верное равенство
. Подставим решение в уравнение, которое обращается в верное равенство  . Сгруппируем члены, вынося общий множитель за скобку:
. Сгруппируем члены, вынося общий множитель за скобку: .
. . Выразим
. Выразим  ;
;  ; разделим переменные и проинтегрируем
; разделим переменные и проинтегрируем  . Тогда
. Тогда  . При известной функции
. При известной функции  интеграл вычислим. Возьмем частное решение при
интеграл вычислим. Возьмем частное решение при  .
. . Значит
. Значит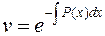 .
. . Подставив найденную функцию
. Подставив найденную функцию  ,
,  ;
;  . Ищем решение в виде
. Ищем решение в виде  ;
;  .
. .
. . Тогда для нахождения u останется простое уравнение
. Тогда для нахождения u останется простое уравнение  .
. как
как  . Получим
. Получим  . Разделим переменные
. Разделим переменные  . Проинтегрируем это равенство
. Проинтегрируем это равенство 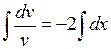 . Взяв в качестве функции
. Взяв в качестве функции  или
или 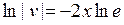 . Воспользовавшись свойством логарифмов, получим
. Воспользовавшись свойством логарифмов, получим  , откуда
, откуда  . Подставим функцию
. Подставим функцию  ; умножим обе части этого равенства на
; умножим обе части этого равенства на  :
:  и представим
и представим  ; разделим переменные
; разделим переменные  и проинтегрируем его
и проинтегрируем его  . Получим функцию
. Получим функцию  . Тогда общее решение исходного уравнения
. Тогда общее решение исходного уравнения  или
или  . Из начальных условий
. Из начальных условий  ;
;  . Итак, решение задачи Коши
. Итак, решение задачи Коши  . ►
. ► .
. . Будем искать решение в виде
. Будем искать решение в виде  . Сгруппируем второй и третий члены левой части, вынесем u за скобку и составим систему
. Сгруппируем второй и третий члены левой части, вынесем u за скобку и составим систему
 ,
,  .
. .
.  или
или .
. ; 2)
; 2)  .
. . Отсюда
. Отсюда  ,
,  . Функция v найдена. Подставим ее во второе уравнение системы и найдем u.
. Функция v найдена. Подставим ее во второе уравнение системы и найдем u. . Разделим обе части уравнения на
. Разделим обе части уравнения на  :
:  .
. или
или  .
.  .
.  .
. и получим
и получим  . Окончательно получаем:
. Окончательно получаем:  .►
.► ,
,
 конкретные значения, то получим частное решение уравнения.
конкретные значения, то получим частное решение уравнения. , …,
, …,  .
.
 ,
, ,
, .
. .
. .
.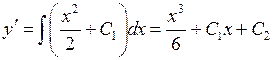 .
. .►
.► .
. . Воспользуемся формулой двойного угла
. Воспользуемся формулой двойного угла  и сократив дробь в правой части на
и сократив дробь в правой части на  , получим
, получим  . Проинтегрируем трижды это уравнение.
. Проинтегрируем трижды это уравнение. .
. .
. .►
.► .
. , тогда
, тогда  .
. .
. . Подставим в уравнение
. Подставим в уравнение .
. и проинтегрируем.
и проинтегрируем. .
. подставим значения
подставим значения  и
и  . Откуда
. Откуда  . Вернемся к полученному равенству:
. Вернемся к полученному равенству:  или
или  . Это простейшее дифференциальное уравнение.
. Это простейшее дифференциальное уравнение.  . Для нахождения
. Для нахождения 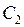 подставим
подставим 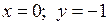 :
: 
 . Таким образом, частное решение примет вид
. Таким образом, частное решение примет вид  . Задача Коши решена. ►
. Задача Коши решена. ►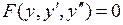
 , тогда
, тогда , но
, но  , отсюда
, отсюда  .
. .
. . Делаем замену
. Делаем замену 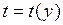 .
. 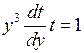 . Разделим переменные
. Разделим переменные  и проинтегрируем
и проинтегрируем .
.  .
. и для функции y получаем дифференциальное уравнение с разделяющимися переменными
и для функции y получаем дифференциальное уравнение с разделяющимися переменными 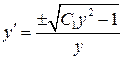 или
или  . Разделим переменные
. Разделим переменные  . Так как
. Так как  , то
, то  .
.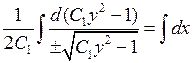 .
. или
или  . ►
. ►
 Комплексным числом c называется упорядоченная пара действительных чисел и обозначается
Комплексным числом c называется упорядоченная пара действительных чисел и обозначается  . Комплексное число можно изобразить точкой на координатной плоскости (см. рисунок). Действительное число a называется действительной частью комплексного числа и обозначается
. Комплексное число можно изобразить точкой на координатной плоскости (см. рисунок). Действительное число a называется действительной частью комплексного числа и обозначается 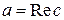 . Действительное число b называется мнимой частью комплексного числа и обозначается
. Действительное число b называется мнимой частью комплексного числа и обозначается 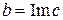 . Суммой и произведением двух комплексных чисел
. Суммой и произведением двух комплексных чисел 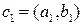 и
и  являются комплексные числа, которые определяются следующим образом:
являются комплексные числа, которые определяются следующим образом: ,
,  .
. .
.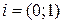 . Оно удовлетворяет соотношению
. Оно удовлетворяет соотношению  . Каждое комплексное число
. Каждое комплексное число  действительного числа
действительного числа  . Запись
. Запись  называются сопряженными комплексными числами.
называются сопряженными комплексными числами. . Сначала вычислим дискриминант
. Сначала вычислим дискриминант  .
. , то уравнение имеет два разных действительных корня
, то уравнение имеет два разных действительных корня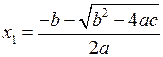 и
и  .
.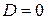 , то уравнение имеет два одинаковых действительных корня (или один корень кратности два)
, то уравнение имеет два одинаковых действительных корня (или один корень кратности два)  .
. , то уравнение имеет два сопряженных комплексных корня
, то уравнение имеет два сопряженных комплексных корня ,
,  .
. .
. уравнение имеет два разных действительных корня
уравнение имеет два разных действительных корня  и
и  .►
.►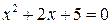 .
. . Так как
. Так как  ,
,  ,
, является действительной частью, а
является действительной частью, а  - мнимой. ►
- мнимой. ►
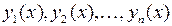 – линейно независимые частные решения уравнения, то
– линейно независимые частные решения уравнения, то 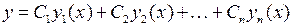 есть общее решение этого уравнения, где
есть общее решение этого уравнения, где 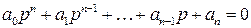 .
.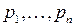 . В случае различных корней фундаментальная система решений имеет вид:
. В случае различных корней фундаментальная система решений имеет вид: 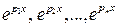 .
.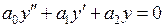
 – действительные числа.
– действительные числа. – частные решения, то
– частные решения, то 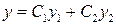 , где
, где  – любые числа, тоже решение данного уравнения. Но для того, чтобы из частных решений
– любые числа, тоже решение данного уравнения. Но для того, чтобы из частных решений 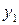 и
и 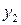 можно было сформировать общее решение, нужно чтобы функции
можно было сформировать общее решение, нужно чтобы функции  , где
, где 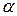 – некоторое число, отличное от нуля.
– некоторое число, отличное от нуля.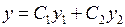 , где
, где 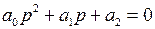 .
.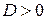 , то есть два действительных и различных корня
, то есть два действительных и различных корня  , тогда частными решениями дифференциального уравнения будут функции
, тогда частными решениями дифференциального уравнения будут функции 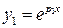 и
и  . При
. При  эти функции нельзя связать равенством
эти функции нельзя связать равенством  , где
, где 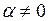 . Следовательно, эти функции линейно независимы и образуют фундаментальную систему решений уравнения. Тогда его общее решение будет иметь вид
. Следовательно, эти функции линейно независимы и образуют фундаментальную систему решений уравнения. Тогда его общее решение будет иметь вид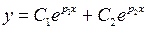 ,
,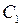 и
и 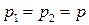 , тогда частными решениями дифференциального уравнения будут функции
, тогда частными решениями дифференциального уравнения будут функции 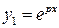 и
и 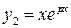 , а его общее решение имеет вид
, а его общее решение имеет вид 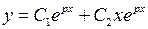 .
.


