
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение линейных неоднородных дифференциальных уравнений с постоянными коэффициентами и специальными
ПРАВЫМИ ЧАСТЯМИ Сведения из теории Уравнение вида
где
где Для нахождения
где Частное решение
где
Рассмотрим некоторые частные случаи: 1. Пусть
2. Пусть
3. Если
4. Пусть правая часть уравнения представляет собой сумму двух функций
Примеры решения задач 1. Решить уравнение ◄ Это линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами. Соответствующее линейное однородное уравнение: Правая часть неоднородного уравнения – многочлен второй степени, частный случай правой части вида с
Представим левую часть в виде многочлена второй степени:
Приравняв коэффициенты при одинаковых степенях
Таким образом,
Общее решение имеет вид
2. Решить уравнение ◄ Используя решение предыдущего примера, запишем
Составим
Приравниваем коэффициенты при одинаковых степенях
Общее решение
3. Решить уравнение ◄ Найдем
Приравнивая коэффициенты при Общее решение
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.89.85 (0.012 с.) |
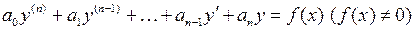 ,
, – постоянные действительные числа, называется линейным неоднородным дифференциальным уравнением с постоянными коэффициентами n-го порядка, решением которого является функция
– постоянные действительные числа, называется линейным неоднородным дифференциальным уравнением с постоянными коэффициентами n-го порядка, решением которого является функция ,
,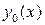 общее решение линейного однородного уравнения,
общее решение линейного однородного уравнения, 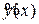 частное решение.
частное решение. – функция, являющаяся правой частью уравнения имеет вид
– функция, являющаяся правой частью уравнения имеет вид ,
, ,
,  – многочлены степеней k и l соответственно.
– многочлены степеней k и l соответственно. такого уравнения можно искать в виде
такого уравнения можно искать в виде ,
,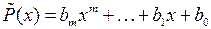 ,
,  – многочлены с неопределенными (буквенными) коэффициентами степени
– многочлены с неопределенными (буквенными) коэффициентами степени  ; показатель
; показатель  , если корни характеристического уравнения не совпадают с
, если корни характеристического уравнения не совпадают с  , и
, и  равно кратности корня p характеристического уравнения, если
равно кратности корня p характеристического уравнения, если 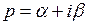 . Заметим, что при решении конкретных задач коэффициенты многочленов
. Заметим, что при решении конкретных задач коэффициенты многочленов  и
и  обычно удобнее обозначать не одной буквой с индексом, как выше, а разными буквами, например
обычно удобнее обозначать не одной буквой с индексом, как выше, а разными буквами, например 
 , где
, где  – многочлен степени n. Тогда частное решение
– многочлен степени n. Тогда частное решение  можно представить в виде
можно представить в виде  , где
, где 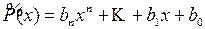 – многочлен той же степени, что и
– многочлен той же степени, что и  , а r – число корней характеристического уравнения, равных нулю.
, а r – число корней характеристического уравнения, равных нулю. , тогда
, тогда 
 , где r – число корней характеристического уравнения, равных α.
, где r – число корней характеристического уравнения, равных α. включает в себя функции
включает в себя функции  и
и  , то этот случай рассматривался выше в общем виде.
, то этот случай рассматривался выше в общем виде. , каждая из которых соответствует виду, тогда решение уравнения имеет вид:
, каждая из которых соответствует виду, тогда решение уравнения имеет вид:  , где
, где  и
и 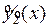 – частные решения уравнения, соответствующие
– частные решения уравнения, соответствующие  и
и  . Количество слагаемых в правой части может быть любым.
. Количество слагаемых в правой части может быть любым. .
. . Его характеристическое уравнение
. Его характеристическое уравнение  имеет корни
имеет корни  , тогда
, тогда  .
.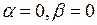 . Так как
. Так как  , а характеристическое уравнение не имеет корня равного 0, то
, а характеристическое уравнение не имеет корня равного 0, то  , где A, B, C неизвестные коэффициенты, которые надо найти. Подставляя
, где A, B, C неизвестные коэффициенты, которые надо найти. Подставляя  и
и  в исходное уравнение, получим
в исходное уравнение, получим .
.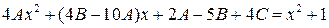 .
. в левой и правой частях, получим систему
в левой и правой частях, получим систему  .
. .
. .►
.► .
. – многочлен первой степени, умноженный на
– многочлен первой степени, умноженный на  , где
, где  , то
, то 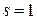 , так как
, так как  . Вычислим его производные и подставим в уравнение, оформив эти процедуры в виде следующей схемы, где слева коэффициенты при функции и ее производных в дифференциальном уравнении
. Вычислим его производные и подставим в уравнение, оформив эти процедуры в виде следующей схемы, где слева коэффициенты при функции и ее производных в дифференциальном уравнении





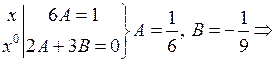
 .
.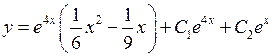 . ►
. ► .
. имеет корни
имеет корни  ,
, 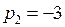 .
.  . Для составления
. Для составления  ;
;  .
.  . Но таких чисел нет среди корней характеристического уравнения, следовательно,
. Но таких чисел нет среди корней характеристического уравнения, следовательно,  .
.  (A и B – многочлены нулевой степени, что соответствует коэффициенту 1 в правой части).
(A и B – многочлены нулевой степени, что соответствует коэффициенту 1 в правой части).


 или
или

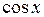 и
и  в левой и правой частях этого равенства, получаем
в левой и правой частях этого равенства, получаем 
 .
. .►
.►


