
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные уравнения первого порядка.
Уравнение Бернулли Сведения из теории Уравнение вида
называется линейным уравнением первого порядка. Если
Уравнение вида
называется уравнением Бернулли. Уравнения и могут быть решены методом Бернулли, который заключается в нахождении решения
Функцию Вспомним, что
При таком подборе функции Примеры решения задач 1. Решить задачу Коши: ◄ Уравнение имеет вид, то есть это линейное уравнение, где
Функцию Решим сначала уравнение 2. Решить уравнение
◄ Приведем уравнение к виду:
Решаем первое уравнение с разделяющимися переменными
Пусть
По свойствам логарифмов 1) Из последнего равенства получим
Вернемся к решению уравнения
Дифференциальные уравнения Высших порядков Основные понятия Сведения из теории Общий вид дифференциального уравнения n -го порядка:
где x – независимая переменная, y – искомая функция, зависящая от x. В общем случае функция
и называется общим интегралом или общим решением уравнения. Если придать каждой произвольной постоянной Чтобы из общего решения выделить одно частное решение, необходимо задать начальные условия:
Рассмотрим некоторые частные случаи решения уравнения, где n больше единицы.
2.2. Простейшее дифференциальное уравнение n -го порядка Сведения из теории Дифференциальное уравнение вида
решается n- кратным интегрированием:
…………..
Примеры решения задач 1. Решить уравнение ◄
2. Решить уравнение ◄ Приведем уравнение к виду.
Уравнение второго порядка,
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.96 (0.016 с.) |

 , то получаем линейное однородное уравнение
, то получаем линейное однородное уравнение .
. ,
,  .
. в виде произведения двух функций
в виде произведения двух функций  и
и  . Если
. Если  , то
, то  . Подставим решение в уравнение, которое обращается в верное равенство
. Подставим решение в уравнение, которое обращается в верное равенство  . Сгруппируем члены, вынося общий множитель за скобку:
. Сгруппируем члены, вынося общий множитель за скобку: .
. . Выразим
. Выразим  ;
;  ; разделим переменные и проинтегрируем
; разделим переменные и проинтегрируем  . Тогда
. Тогда  . При известной функции
. При известной функции  интеграл вычислим. Возьмем частное решение при
интеграл вычислим. Возьмем частное решение при  .
. . Значит
. Значит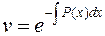 .
. . Подставив найденную функцию
. Подставив найденную функцию  .
. ,
,  .
. ;
;  . Ищем решение в виде
. Ищем решение в виде  ;
;  :
:  .
. .
. . Тогда для нахождения u останется простое уравнение
. Тогда для нахождения u останется простое уравнение  .
. как
как  . Получим
. Получим  . Разделим переменные
. Разделим переменные  . Проинтегрируем это равенство
. Проинтегрируем это равенство 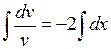 . Взяв в качестве функции
. Взяв в качестве функции  или
или 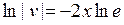 . Воспользовавшись свойством логарифмов, получим
. Воспользовавшись свойством логарифмов, получим  , откуда
, откуда  . Подставим функцию
. Подставим функцию  ; умножим обе части этого равенства на
; умножим обе части этого равенства на  :
:  и представим
и представим  ; разделим переменные
; разделим переменные  и проинтегрируем его
и проинтегрируем его  . Получим функцию
. Получим функцию  . Тогда общее решение исходного уравнения
. Тогда общее решение исходного уравнения  или
или  . Из начальных условий
. Из начальных условий  ;
;  . Итак, решение задачи Коши
. Итак, решение задачи Коши  . ►
. ► .
. . Будем искать решение в виде
. Будем искать решение в виде  . Сгруппируем второй и третий члены левой части, вынесем u за скобку и составим систему
. Сгруппируем второй и третий члены левой части, вынесем u за скобку и составим систему
 ,
,  .
. .
.  или
или .
. ; 2)
; 2)  .
. . Отсюда
. Отсюда  ,
,  . Функция v найдена. Подставим ее во второе уравнение системы и найдем u.
. Функция v найдена. Подставим ее во второе уравнение системы и найдем u. . Разделим обе части уравнения на
. Разделим обе части уравнения на  :
:  .
. или
или  .
.  .
.  .
. и получим
и получим  . Окончательно получаем:
. Окончательно получаем:  .►
.► ,
,
 конкретные значения, то получим частное решение уравнения.
конкретные значения, то получим частное решение уравнения. ,
,  ,
,  , …,
, …,  .
.
 ,
, ,
, .
. .
. .
.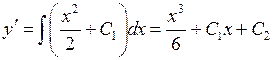 .
. .►
.► .
. . Воспользуемся формулой двойного угла
. Воспользуемся формулой двойного угла  и сократив дробь в правой части на
и сократив дробь в правой части на  , получим
, получим  . Проинтегрируем трижды это уравнение.
. Проинтегрируем трижды это уравнение. .
. .
. .►
.►


