
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные неоднородные дифференциальные уравнения ВТОРОго порядка.
Метод вариации произвольной постоянной Сведения из теории Метод вариации произвольных постоянных (метод Лагранжа) решения линейного неоднородного уравнения
является универсальным (для любой Для линейного уравнения второго порядка, общее решение соответствующего ему однородного уравнения Решение линейного неоднородного уравнения ищется в виде
получающемся из общего решения однородного уравнения заменой произвольных постоянных
Пусть Интегрируя эти равенства, находим:
где Подставляя найденные
Примеры решения задач
1. Решить уравнение ◄ Решим однородное уравнение
Система для этого уравнения имеет вид
Умножим обе части каждого уравнения системы на
Из первого уравнения системы выразим Умножим обе части этого уравнения на
Итак,
Подставив в уравнение Итак,
Подставляем
Раскрыв скобки и перегруппировав, получим общее решение в виде
где A и B произвольные постоянные. ►
Системы дифференциальных уравнений Сведения из теории Система вида
где x – независимая переменная, Решением такой системы являются функции Для двух неизвестных функций система имеет вид:
Примеры решения задач 1. Решить систему ◄ Продифференцируем первое уравнение системы:
Ответ:
ОПЕРАЦИОННЫЙ МЕТОД РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Сведения из теории
Если
это соответствие записывают так
В приложении приведена таблица соответствий между оригиналами и изображениями. Приведём основные правила (свойства) преобразования Лапласа, которыми будем пользоваться.
Линейность
Если
то для любых чисел
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.142.189 (0.008 с.) |
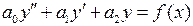
 ).
). будет
будет  , где
, где 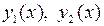 является фундаментальной системой решений и зависит от корней характеристического уравнения.
является фундаментальной системой решений и зависит от корней характеристического уравнения. ,
, на функции
на функции  . Нахождение функций
. Нахождение функций 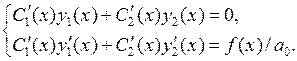
 ,
,  – решение этой системы.
– решение этой системы. ,
,  ,
,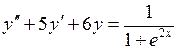 .
. . Характеристическое уравнение
. Характеристическое уравнение  .
.  .
. .
.
 . Получим
. Получим
 и подставим во второе. Получим:
и подставим во второе. Получим:  или
или  .
. :
:  . Проинтегрируем это равенство. Тогда
. Проинтегрируем это равенство. Тогда  . Вычислим
. Вычислим 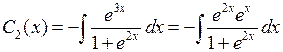 . Сделаем замену
. Сделаем замену  , тогда
, тогда  и
и  .
. .
. , получим
, получим  . Интегрируя, находим:
. Интегрируя, находим:  .
. .
. и
и  и получаем общее решение нашего уравнения
и получаем общее решение нашего уравнения .
. ,
,
 неизвестные функции независимой переменной x называется нормальной системой.
неизвестные функции независимой переменной x называется нормальной системой. . Одним из методов решения системы является метод исключения неизвестных.
. Одним из методов решения системы является метод исключения неизвестных.

 . Заменим
. Заменим  правой частью из второго уравнения:
правой частью из второго уравнения:  , а затем заменим v выражением, полученным из первого
, а затем заменим v выражением, полученным из первого или
или  .
. . Получили линейное однородное уравнение второго порядка. Решим его:
. Получили линейное однородное уравнение второго порядка. Решим его:  .
.  .
.
 ►
►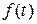 функция- оригинал,
функция- оригинал,  - изображение функции
- изображение функции 
 .
. ,
,
 .
.


