Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило изображения производных ⇐ ПредыдущаяСтр 7 из 7
Производные функции Если
Это означает, что операции дифференцирования оригиналов соответствует гораздо более простая операция умножения на аргумент p для изображений.
Операционный метод решения линейных Дифференциальных уравнений с постоянными коэффициентами Рассмотрим задачу Коши для линейного дифференциального уравнения второго порядка с постоянными коэффициентами[1]
применим к обеим частям уравнения преобразование Лапласа. Пусть
Вместо линейного дифференциального уравнения для оригинала
Найдя по изображению Примеры решения задач 1. Найти изображения следующих функций: а) ◄ а) По формуле 3 таблицы б) По формуле 4 таблицы в) По формуле 2 таблицы г) По формулам 5 и 6 таблицы
По свойству линейности д) По формулам 7 и 8 таблицы
По свойству линейности
2. По заданным изображениям найти их оригиналы: а) ◄а) Подгоним
Итак, б) По формулам 7 и 6 По свойству линейности в) Для нахождения оригинала дроби
Её разложение в сумму простейших дробей имеет вид
где коэффициенты
и приравняем числители
Положим здесь p равным корням знаменателя
Итак,
По формуле (3) таблицы
Из и, учитывая линейность преобразования Лапласа, получаем
3. Найти решение задачи Коши
◄ Пусть
По формуле (3) таблицы
Отсюда
Оригинал этой функции – искомое решение найден в примере 2: 4. Найти решение задачи Коши
◄ Пусть
Откуда
Полученную дробь разложим на простейшие. Заметим, что множитель
Запишем правую часть равенства в виде стандартного многочлена (то есть расположенного по убывающим степеням p):
Используя теорему о равенстве многочленов, приравняем коэффициенты при одинаковых степенях левой и правой частей уравнения:
По формулам (6), (3) и (4) таблицы
Список литературы 1. Бугров, Я.С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1985. – 464с.
2. Пискунов, П.С. Дифференциальное и интегральное исчисление для втузов». Т. 2, 13 изд., М.: Наука, 1985. - 560 с.
3. Сборник задач по высшей математике для вузов. Ч.2. Специальные разделы математического анализа / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1986. – 366 с.
4. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 5-е изд., исп. – М.: Высшая школа, 1999. – 304 с.
5. Краснов, М.Л. Сборник задач по дифференциальным уравнениям / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. - М.: Высшая школа, 1978, - 388с.
ПРИЛОЖЕНИЕ А Таблица соответствий оригиналов и изображений
Задания для контрольной работы
1-11. Решить дифференциальные уравнения.
12. Решить систему дифференциальных уравнений.
13. Найти изображение.
14. Решить задачу Коши операционным методом. Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Вариант 13
Вариант 14
Вариант 15
Вариант 16
Вариант 17
Вариант 18
Вариант 19
Вариант 20
Вариант 21
Вариант 22
Вариант 23
Вариант 24
Вариант 25
Вариант 26
Вариант 27
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.12.205 (0.063 с.) |
 аргумента t (имеющего смысл времени) по традиции, идущей в механике от Ньютона, будем обозначать точкой:
аргумента t (имеющего смысл времени) по традиции, идущей в механике от Ньютона, будем обозначать точкой:  – первая производная,
– первая производная,  – вторая производная и т.д.
– вторая производная и т.д. , то
, то

 .
. . Воспользуемся линейностью преобразования Лапласа, формулами для изображения производных и начальных условий. Получим уравнение для нахождения неизвестного нам изображения
. Воспользуемся линейностью преобразования Лапласа, формулами для изображения производных и начальных условий. Получим уравнение для нахождения неизвестного нам изображения 

 .
. . Оно легко решается:
. Оно легко решается: .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
. , а по формуле 1 таблицы
, а по формуле 1 таблицы  . По свойству линейности
. По свойству линейности  . Таким образом, изображение функции
. Таким образом, изображение функции  .
. .
. .
. ,
,  .
. .
. ,
,  .
. .►
.► ; б)
; б)  ; в)
; в)  .
.
 .
. – оригинал для
– оригинал для  .
. ,
,  .
. .
.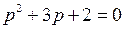 имеет корни
имеет корни  и
и  . Таким образом,
. Таким образом,  и дробь имеет вид
и дробь имеет вид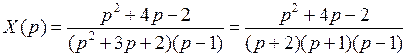 .
. ,
, подлежат определению (каждому множителю в знаменателе в левой части соответствует простейшая дробь в правой части). Приведём правую часть этого равенства к общему знаменателю
подлежат определению (каждому множителю в знаменателе в левой части соответствует простейшая дробь в правой части). Приведём правую часть этого равенства к общему знаменателю 

 .
.

 .
. .
. .►
.► .
. – искомое решение, а
– искомое решение, а 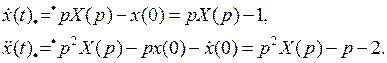
 . Применим к обеим частям уравнения преобразование Лапласа, используя его линейность и найденные изображения. Получим уравнение для нахождения
. Применим к обеим частям уравнения преобразование Лапласа, используя его линейность и найденные изображения. Получим уравнение для нахождения  или
или  ,
, ,
, .
. .
. . ►
. ► .
. . По формуле (4) таблицы
. По формуле (4) таблицы  . Применим к обеим частям уравнения преобразование Лапласа
. Применим к обеим частям уравнения преобразование Лапласа или
или  .
. .
. не имеет действительных корней и на линейные множители не раскладывается, а корень
не имеет действительных корней и на линейные множители не раскладывается, а корень  имеет кратность 2. В этом случае разложение
имеет кратность 2. В этом случае разложение  .
. .
. .
.

 .
. .
. .
. .►
.►














 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
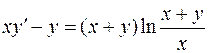 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

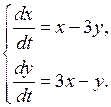


 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
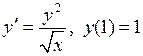 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
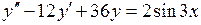 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




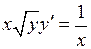 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
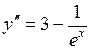 .
.
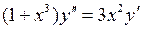 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.


 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
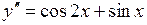 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
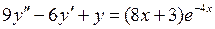 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.




 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
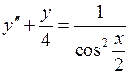



 .
.
 .
.
 .
.
 .
.
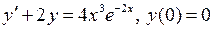 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
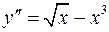 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.


 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.