
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Не содержащее явно искомой функции
Сведения из теории Рассмотрим дифференциальное уравнение второго порядка
Решить это уравнение можно понижением порядка. Для этого введем замену Примеры решения задач 1. Решить задачу Коши ◄ Так как уравнение не содержит зависимой переменной y, то для понижения порядка введем замену
Разделим переменные
Для нахождения
Уравнение второго порядка, не содержащее явно независимой переменной x Сведения из теории
– дифференциальное уравнение второго порядка этого типа. Понижаем порядок с помощью замены
Примеры решения задач
1. Решить дифференциальное уравнение ◄ Уравнение не содержит явно независимой переменной
Таким образом, Проинтегрируем уравнение:
Комплексные числа Сведения из теории
Действительные числа a содержатся в классе комплексных чисел в качестве пар Мнимой единицей называется число
Два комплексных числа Примеры решения задач
Вспомним формулы для решения квадратного уравнения Если
Если Если
1. Решить квадратное уравнение ◄ Вычислим дискриминант для данного уравнения: 2. Решить квадратное уравнение ◄
для которых
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.007 с.) |
 .
. , тогда
, тогда  .
. .
. . Подставим в уравнение
. Подставим в уравнение .
. и проинтегрируем.
и проинтегрируем. .
. подставим значения
подставим значения  и
и  . Откуда
. Откуда  . Вернемся к полученному равенству:
. Вернемся к полученному равенству:  или
или  . Это простейшее дифференциальное уравнение.
. Это простейшее дифференциальное уравнение.  . Для нахождения
. Для нахождения 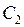 подставим
подставим 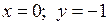 :
: 
 . Таким образом, частное решение примет вид
. Таким образом, частное решение примет вид  . Задача Коши решена. ►
. Задача Коши решена. ►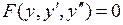
 , тогда
, тогда , но
, но  , отсюда
, отсюда  .
. .
. . Делаем замену
. Делаем замену 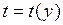 .
. 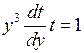 . Разделим переменные
. Разделим переменные  и проинтегрируем
и проинтегрируем .
.  .
. и для функции y получаем дифференциальное уравнение с разделяющимися переменными
и для функции y получаем дифференциальное уравнение с разделяющимися переменными 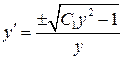 или
или  . Разделим переменные
. Разделим переменные  . Так как
. Так как  , то
, то  .
.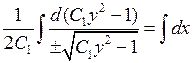 .
. или
или  . ►
. ►
 Комплексным числом c называется упорядоченная пара действительных чисел и обозначается
Комплексным числом c называется упорядоченная пара действительных чисел и обозначается  . Комплексное число можно изобразить точкой на координатной плоскости (см. рисунок). Действительное число a называется действительной частью комплексного числа и обозначается
. Комплексное число можно изобразить точкой на координатной плоскости (см. рисунок). Действительное число a называется действительной частью комплексного числа и обозначается 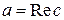 . Действительное число b называется мнимой частью комплексного числа и обозначается
. Действительное число b называется мнимой частью комплексного числа и обозначается 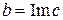 . Суммой и произведением двух комплексных чисел
. Суммой и произведением двух комплексных чисел 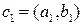 и
и  являются комплексные числа, которые определяются следующим образом:
являются комплексные числа, которые определяются следующим образом: ,
,  .
. .
.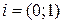 . Оно удовлетворяет соотношению
. Оно удовлетворяет соотношению  . Каждое комплексное число
. Каждое комплексное число  действительного числа
действительного числа  . Запись
. Запись  называются сопряженными комплексными числами.
называются сопряженными комплексными числами. . Сначала вычислим дискриминант
. Сначала вычислим дискриминант  .
. , то уравнение имеет два разных действительных корня
, то уравнение имеет два разных действительных корня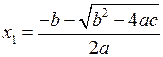 и
и  .
.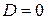 , то уравнение имеет два одинаковых действительных корня (или один корень кратности два)
, то уравнение имеет два одинаковых действительных корня (или один корень кратности два)  .
. , то уравнение имеет два сопряженных комплексных корня
, то уравнение имеет два сопряженных комплексных корня ,
,  .
. .
. уравнение имеет два разных действительных корня
уравнение имеет два разных действительных корня  и
и  .►
.►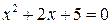 .
. . Так как
. Так как  ,
,  ,
, является действительной частью, а
является действительной частью, а  - мнимой. ►
- мнимой. ►


