
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сборник задач по расчету энергосиловыхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сборник задач по расчету энергосиловых Изменение длины дуги захвата от обжатия и диаметра валков
2. Вычисляем угол захвата металла валками по формуле (табл. 1.2)
Таблица 1.2. Изменение угла захвата от обжатия и диаметра валков
3. Используя данные табл. 1.1 и 1.2, строим графики указанных зависимостей (рис. 1.1. и 1.2.).
Рис. 1.1. Зависимость длины дуги захвата Рис. 1.2. Зависимость угла захвата от обжатия и диаметра валков от обжатия и диаметра валков
УСЛОВИЯ ЗАХВАТА ПОЛОСЫ ВАЛКАМИ
Алгоритм расчета и проверки условий захвата Полосы валками Алгоритм расчета условий захвата полосы валками представляет собой определенную последовательность вычислений и их логическую проверку. Определяем абсолютное обжатие полосы: D h = h0 – h1 . Вычисляем угол захвата: α = Рассчитываем коэффициент контактного трения по уравнениям Гелеи: - для шлифованных чугунных или стальных валков f = 0,82 - 0,0005 Т - 0,056 v; - для чугунных валков f = 0,94 - 0,0005 Т - 0,056 v; - для стальных валков f = 1,05- 0,0005 Т - 0,056 v, где Т – температура полосы, ºС; v – скорость прокатки, м/с. 4. Принимаем, что угол трения b в радианах равен коэффициенту контактного трения f, т. е. b = f. 5. Проверяем режим обжатия на условие захвата полосы валками а) если D = (a - b) £ 0, то захват происходит (a £ b); б ) если D > 0, то захват невозможен (a > b). Примеры расчета Пример 1. На стане с рабочими чугунными валками диаметром 1000 мм за один проход предполагается прокатать заготовку толщиной h0 = 180 мм до толщины h1 = 100 мм на скорости v = 3 м/с при температуре полосы, равной 1200ºC. Определить, произойдет ли захват полосы валками. Решение. 1. Определяем абсолютное обжатие полосы Dh = Н0 – Н1 = 180 –100 – 80 мм. 2. Вычисляем угол захвата
3. Рассчитываем коэффициент контактного трения по формуле Гелеи
f = 0,94 – 0,0005Т – 0,056 v = 0,94 – 0,0005×1200 – 0,056×3 = 0,172. 4. Принимаем угол трения равным коэффициенту контактного трения b = f = 0,172 рад. 5. Проверяем на условие захвата заготовки валками. Итак, для захвата заготовки валками необходимо, чтобы угол захвата a не превышал угол трения, т.е. a £ b. В нашем случае a = 0,4 рад > b = 0,17 рад. Вывод. Захват полосы не произойдет, так как режим обжатий или технологические переменные подобраны неудачно. Для обеспечения процесса прокатки требуется корректировка их значений.
Пример 2. На обжимном стане дуо 850 требуется прокатать заготовку толщиной h0 = 150 мм со скоростью v = 2 м/с, нагретую до температуры Т = 1100ºC, за один проход с максимально возможным по условию захвата металла обжатием. Определить, до какой минимальной толщины можно обжать заготовку, если использовать как чугунные, так и стальные валки. Решение. 1. Рассчитаем по формуле Гелеи коэффициент контактного трения для чугунных (индекс «ч») и стальных (индекс «с») валков: fч = 0,94 – 0,0005 T – 0,056 v = 0,94 – 0,0005×1100 – 0,056×2 = 0,278; fс = 1,05 – 0,0005 T – 0,056 v = 1,05 – 0,0005×1100 – 0,056×2 = 0,388. 2. Угол трения численно равен коэффициенту контактного трения b = fч = 0,278 рад = 16 град, b = fс = 0,388 рад = 22 град. 3. Используя условие захвата металла валками (a £ b), определяем, что максимальная величина угла a может быть равна величине угла b, т.е. aч = b = 0,278 рад, aс = b = 0,388 рад. 4. Используя формулу для расчета угла захвата Dhч = R a2 = 425 × 0,2782 ≈ 33 мм, Dhс = R a2 = 425 × 0,3882 ≈ 64 мм. Таким образом, при использовании чугунных валков максимально возможное по условию захвата металла обжатие в проходе Dhч должно быть менее 33 мм, а при использовании стальных валков Dhс не должно превышать 64 мм. 5. Вычисляем толщину заготовки после прохода h1ч = h0 – Dh = 150 – 32 = 118 мм, h1с = h0 – Dh = 150 – 64 = 86 мм, Следовательно, при использовании чугунных валков можно прокатать за один проход заготовку толщиной 118 мм, а на стальных валках 86 мм. Вывод. Стальные валки обладают большей захватывающей способностью по сравнению с чугунными валками.
Пример 3. На блюминге 1500 (валки стальные) прокатали заготовку размером 640×820×2400 мм с относительным обжатием в проходе 11,1 %, при температуре раската 1200ºС и скорости 2,0 м/с. Проверить режим на условие захвата, определить начальные размеры заготовки и геометрические параметры очага деформации.
Решение. 1. Определяем начальную толщину заготовки h0 = 2. Вычисляем абсолютное обжатие Dh = h0 – h1 = 720 – 640 = 80 мм. 3. Определяем длину дуги захвата
4. Находим угол захвата
5. Определяем коэффициент трения f = 1,05 – 0,0005Т – 0,056 v = 1,05 – 0,0005×1200 – 0,056×2 = 0,338. Вывод. Захват металла валками возможен, т. к. a = 0,327 рад < b = 0,338 рад. 6. Вычисляем уширение раската Db = 0,4e ld = 0,4× 0,111×244,95 = 10,88» 11 мм. 7. Определяем начальную ширину заготовки b0 = b1 – Db = 820 – 11 = 809 мм. 8. Находим начальную длину слитка из условия постоянства объема L0 = 9. Определяем площадь контакта металла с валками
Ответ. Начальные размеры слитка 720×809×2160 мм.
Пример 4. До какой толщины можно обжимать заготовку с исходной толщиной 560 мм в клети с рабочими валками диаметром 1020 мм, если коэффициент контактного трения равен 0,304. Решение. 1. Считая, что угол трения численно равен коэффициенту контактного трения f = b, получим b = a = 0,304. 2. Вычисляем абсолютное обжатие заготовки Dh = R a2 = 510 × 0,3042 = 47,26 = 47,3 мм. 3. Определяем, до какой толщины можно обжимать полосу h1 = h0 – Dh = 560 – 47,3 = 512,7» 513 мм.
Пример 5. Определить какой должен был бы быть диаметр рабочих валков, изготовленных из кованой стали и из отбеленного чугуна, обеспечивающих условие захвата заготовки c начальной толщиной 450 мм при относительном обжатии 55%. Температура металла 1250 0С, скорость прокатки 3,5 м/с. Решение. 1. Определяем коэффициент трения для стальных и чугунных валков fc = 1,05 – 0,0005 T – 0,056 v = 1,05 – 0,0005×1250 – 0,056×3,5 = 0,229; fч = 0,94 – 0,0005 T – 0,056 v = 0,94 – 0,0005×1250 – 0,056×3,5 = 0,119. 2. Находим абсолютное обжатие Dh =e h0 = 0,55× 450 = 247,5 мм. 4. Используя формулу угла захвата Dc =
Вывод. Диаметры валков не реальны, так как известно, что максимальный диаметр рабочих валков достигает примерно 1500 мм (блюминг 1500).
Пример 6. Определить максимальное обжатие за проход в чистовой клети ТЛС 3600 с чугунными валками диаметром 800 мм, при котором возможен захват металла. Скорость прокатки 4,82 м/с, температура металла 980ºС. Решение. 1. Определяем коэффициент трения при прокатке f = 0,94 – 0,0005 T – 0,056 v = 0,94 – 0,0005× 980 – 0,056× 4,82 = 0,180. 2. Принимаем, что угол трения численно равен коэффициенту контактного трения, т. е. b = f = 0,180. Тогда угол захвата a = b = 0,180. 3. Используя формулу угла захвата Dhmax =
Пример 7. Лист сечением 32×3200 мм и длиной 7300 мм за один проход прокатали на толстолистовом стане с чугунными валками диаметром 960 мм. Температура листа 920ºС, скорость прокатки 4,8 м/с, коэффициент вытяжки после прохода равен 1,23. Проверить режим на условие захвата металла валками и определить длину листа после прохода. Решение. 1. Определяем толщину листа после прохода (уширение отсутствует)
2. Определяем абсолютное обжатие Dh = h0 – h1 = 32 – 26 = 6 мм. 3. Вычисляем длину дуги захвата
4. Определяем угол захвата металла валками
5. Находим значение коэффициента трения для данного прохода f = 0,94 - 0,0005 T - 0,056 v = 0,94 - 0,0005× 920 - 0,056× 4,8 = 0,211. Вывод. Захват возможен, т. к. a = 0,112 < b = 0,211.
6. Определяем длину листа после прохода L1 = l L0 = 1,23×7300» 8980 мм.
Пример 8. Кованая заготовка массой 8 тонн из стали 10ГН2МФА (r = 7,87 т/м3 ) после гидгосбива печной окалины потерял в массе 3% и с поперечным сечением 650×980 мм за один проход был прокатан в черновой клети ТЛС 4000. Определить возможность захвата металла валками, геометрические размеры очага деформации и размеры заготовки после прокатки, если известно, что скорость прокатки V = 2,68 м/с, относительное обжатие e = 7,23 %, температура металла Т= 1170ºС, валки стальные диаметром 1030 мм. Решение. 1. Определяем массу заготовки после гидросбива печной окалины M = 0,97× 8 = 7,76 т. 2. Определяем длину заготовки перед проходом
3. Находим абсолютное обжатие за проход D h = e h0 = 0,0723 × 650 = 47 мм. 4. Определяем толщину листа после прохода h1 = h0 – Dh = 650 – 47 = 603 мм. 5. Вычисляем длину дуги захвата металла валками
6. Определяем угол захвата металла валками
7. Вычисляем коэффициент трения f = 1,05 – 0,0005 T – 0,056 v = 1,05 – 0,0005 × 1170 – 0,056 × 2,68 = 0,315. 8. Определяем возможность захвата металла валками, т.е. условие a £ b. Вывод. Так как a = 0,302 < b = 0,315, захват возможен. 9. Находим величину уширения раската Db = 0,4 e ld = 0,4×0,0723×155,58 = 4,5 мм. 10. Определяем ширину слитка после прохода b1 = b0 + Db = 980 + 4,5 = 984,5 мм. 11. Рассчитываем площадь контакта металла с валками
12. Вычисляем длину раската после прохода из условия постоянства объема
Вывод. Размеры заготовки после прохода 603×985×1660 мм.
Примеры расчета Пример 1. Полоса толщиной 8,1 мм прокатывается в клети с обжатием 2,7 мм и со скоростью 13,86 м/с выходит из валков. Определить скорость полосы на входе в клеть. Решение. 1. Находим толщину полосы на выходе из клети h1 = h0 - ∆h = 8,1 – 2,7 = 5,4 мм. 2. Вычисляем коэффициент вытяжки λ = 3. Определяем скорость полосы на входе в клеть. Так как v1 = λ v0, то v0 =
Пример 2. Определить скорость движения полосы на входе, выходе из валков и среднюю скорость деформации при прокатке металла на стане с рабочими валками диаметром 300 мм. Условия процесса характеризуются следующими данными: h0 = 2 мм, h1 = 1,5 мм, f = 0,05. Скорость прокатки v = 5 м/с. Решение. 1. Определяем угол захвата a = 2. Так как процесс прокатки простой и захват металла свободный, то принимаем, что угол трения численно равен коэффициенту контактного трения b = f = a = 0,0577 рад. 3. Вычисляем нейтральный угол
4. Определяем опережение по формуле Финка
5. Рассчитываем величину отставания по формуле А.И. Целикова
6. Определяем скорость полосы на входе в зону деформации (в зев валков) v0 = vв (1 – S0) = 5 (1- 0,237) = 3,81 м/с. 7. Вычисляем скорость полосы на выходе из валков: v1 = vв (1 + S1) = 5 (1+ 0,015) = 5,07 м/с. 8. Определяем среднюю скорость деформации полосы по формуле:
Пример 3. Определить скорость рольганга блюминга 1500 после выхода из валков слитка с поперечным сечением 760×1030 мм из стали 08кп. Скорость прокатки 2,86 м/с, абсолютное обжатие 60 мм, температура слитка 1240ºС. Решение. 1. Определяем угол захвата металла валками
2. Вычисляем коэффициент контактного трения f = 1,05 – 0,0005 T – 0,056 V = 1,05 – 0,0005× 1200 – 0,056× 2,86 = 0,290. 3. Принимаем угол трения равным коэффициенту контактного трения, т. е. b = f = 0,290 рад. 4. Вычисляем нейтральный угол
5. Определяем опережение полосы с учетом уширения, используя формулу А.А. Королева S1 = 6. Находим скорость полосы на выходе из валков, которая должна быть равна скорости рольганга v1 = vв (1 + S1) = 2,86(1+ 0,0049) = 2,87 м/с.
Пример 4. Определить скорость прокатки в клети №8 непрерывного 14-ти клетевого стана 320 горячей прокатки, если известно, что из клети № 9 с валками диаметром D9 = 330 мм при числе оборотов валков n9 = 450 об/мин выходит полоса толщиной h9 = 7 мм и шириной b9 = 82 мм. Толщина полосы на выходе из клети № 8 h8 = 9 мм. Прокатка идет без натяжения. Учет уширения обязателен. Решение. 1. Вычисляем абсолютное обжатие полосы в клети № 9: Dh = h0 – h1 = 9 – 7 = 2 мм. 2. По формуле Зибеля находим уширение полосы на выходе из клети №9
3. Определяем ширину полосы на выходе из клети № 8: b8 = b9 – Db9 = 82 – 1,5 = 80,5 мм. 4. Определяем окружную скорость (скорость прокатки) валков в клети №9:
5. Вычисляем константу (постоянную) непрерывного стана: С = Vв9 h9 b9 = 7,77×7×82×1000 = 4460000 мм3/с. 6. Из уравнения постоянства секундных объёмов vв8 h8 b8 = vв9 h9 b9 = С определяем скорость прокатки в клети № 8
Пример 5. Полоса входит в первую клеть чистовой группы НШС горячей прокатки со скоростью 1,30 м/с, что на 5,7% меньше скорости валков. Определить скорость прокатки (скорость валков) в седьмой клети, если известно, что скорости во всех клетях согласованы и суммарный коэффициент вытяжки равен 9,25. Решение. 1. Вычисляем скорость валков (скорость прокатки) в первой клети стана: Vв1 = 2. Определяем скорость прокатки в последней клети стана vв7 = λ vв1 = 9,25 ∙1,38 = 12,77 м/с.
Пример 6. Полоса с поперечным сечением 2,8×2350 мм выходит из предпоследней клети чистовой группы НШС горячей прокатки со скорость 14,96 м/с, что на 4,4% больше скорости валков. Коэффициент натяжения между последней и предпоследней клетью К = 0,91. Определить скорость прокатки и постоянную последней клети. Решение. 1. Определяем скорость валков (прокатки) в предпоследней клети стана:
2. Определяем константу предпоследней клети: Сn-1 = vп h b = 14,96×2,8×2350×1000 = 98400000 мм3/с. 3. Определяем константу последней клети: Cn-1 = К Сn; Сn = Пример 7. Из валков клети №7 чистовой группы клетей широкополосного стана 2000 горячей прокатки со скоростью 23,1 м/с прокатали полосу толщиной 2,5 мм и шириной 1650 мм. Определить скорости прокатки полосы в остальных клетях стана, если известен режим обжатий по клетям, мм: h0 = 25; h1 = 15,8; h2 =10,4; h3 = 7,0; h4 = 4,8; h5 = 3,6; h6 = 2,9. Построить график изменения скорости прокатки по клетям.
Решение. 1. Определяем постоянную непрерывного стана С= v7 b7 h7 = 23,1× 1650× 2,5× 103 = 95300000 м/мм3. 2. Вычисляем скорость прокатки в каждой клети v6 = v4 = v2 = 3. Строим график изменения скорости прокатки по клетям (рис 3.1)
Рис.3.1. Зависимости изменения скорости прокатки по клетям на непрерывном стане
Пример 8. Определить и построить графики влияния переднего натяжения на опережение и скорость выхода переднего конца полосы из листового стана, имеющего диаметр рабочих валков 520 мм. Толщина полосы до прокатки 2,07 мм, после прокатки 1,8 мм, коэффициент контактного трения f = 0,05, предел текучести полосы после прокатки ss1 = 375 МПа, валки вращаются со скоростью vв = 24 м/с. Переднее натяжение изменяется и может принимать следующие значения: s1 = 0,05; 0,1; 0,15; 0,20 ss1. Решение. 1. Вычисляем абсолютное обжатие полосы Dh = h0 – h1 = 2,07 – 1,8 = 0,27 мм. 2. Находим длину дуги захвата металла валками
3. Определяем переднее удельное натяжение полосы: s1 = 0,05 sS1 = 0,05 × 375 = 18,75 МПа; s2 = 0,1 sS1 = 0,1 × 375 = 37,5 МПа; s3 = 0,15 sS1 = 0,15 × 375 = 56,25 МПа; s4 = 0,2 sS1 = 0,2 × 375 = 75 МПа. 4. Находим коэффициенты натяжения заднего и переднего концов полосы: 2К1 = 1,155 sS1 = 1,155 × 375 = 433 МПа; d = x0 = x11 = x13 = 5. Рассчитываем опережение с учетом натяжения: S11 = S12 = S13 = S14 = 6. Определяем скорость выхода металла из валков для каждого случая: vп1 = vв (1+ S11) = 24 (1+0,056) = 25,34 м/с; vп2 = vв (1+ S12) = 24 (1+0,064) = 25,53 м/с; vп3 = vв (1+ S13) = 24 (1+0,072) = 25,73 м/с; vп4 = vв (1+ S14) = 24 (1+0,081) = 25,95 м/с; 7. Строим графики влияния переднего натяжения на опережение и скорость выхода переднего конца полосы из валков клети (рис.3.2), предварительно занеся необходимые данные в таблицу 3.1.
Таблица 3.1. И УШИРЕНИЕ ПОЛОСЫ Примеры расчета Пример 1. В черновой клети ТЛС 5000 прокатывают листовой слиток из стали 12ХН3МДА толщиной 780 мм, нагретый до 1200ºС. Валки стальные, скорость прокатки 2,16 м/с. Определить минимально возможную ширину слитка, при которой уширение будет практически отсутствовать. Решение. 1. Вычисляем коэффициент контактного трения при прокатке слитка f = 1,05 – 0,0005 T – 0,056 v = 1,05 – 0,0005×1200 – 0,056×2,16 = 0,329. 2. Уширение практически отсутствует при условии плоскодеформированной схеме прокатки, когда выполняется следующее неравенство b0 ³
Пример 2. Определить необходимость расчета уширения полосы из стали 45 после прокатки её при следующих условиях: температура прокатки 1180ºС, размеры полосы до прокатки h0 = 100 мм и b0 =120 мм, толщина полосы после прокатки h1 = 60 мм. Рабочие валки из отбеленного чугуна диаметром 300 мм. Скорость прокатки 2,4 м/с. Решение. 1. Находим коэффициент контактного трения при прокатке f = 0,94 – 0,0005 T – 0,056 v = 0,94 – 0,0005×1180 – 0,056×2,4 = 0,215. 2 Уширение необходимо рассчитывать при объемной схеме напряженно-деформированного состояния металла, которое можно определить исходя из неравенства
Неравенство выполняется. Значит необходимо рассчитывать уширение полосы. 3. Определяем абсолютное и относительное обжатие в проходе Dh = h0 – h1 = 100 – 60 = 40 мм; e = 4. Вычисляем длину дуги захвата металла валками
5. Находим величину уширения полосы Db = 0,4 e ld = 0,4 × 0,4 × 109,54 = 17,53 мм» 18 мм. Пример 3. Определить влияние обжатия и диаметра валков на уширение при прокатке полосы толщиной 100 мм в валках диаметром 300, 700 и 1100 мм, если обжатия принимают следующие значения 5, 10, 15, 20 и 25 мм. Построить графики зависимости уширения от обжатия и диаметра валков и проанализировать полученные результаты. Решение. Рассмотрим случай, когда ∆h = 5 мм, а диаметр валков 300 мм. 1. Находим относительное обжатие полосы
2. Вычисляем длину захвата металла валками ld = 3. Определяем величину уширения ∆b = 0,4 ε ld =0,4∙0,05∙27,39 = 0,55 мм. Для остальных случаев прокатки расчеты проводится аналогично. Данные расчета сведены в табл. 4.1 и отображены на рис. 4.1.
Таблица 4.1. ВНЕШНЕЕ ТРЕНИЕ ПРИ ПРОКАТКЕ
Примеры расчета
Пример 1. Определить влияние изменения температуры полосы из стали 09Г2С на условия трения при прокатке ее чугунными и стальными валками. Прокатка ведется с постоянной скоростью 6 м/с; температура прокатки может принимать следующие значения (0С): 800, 900, 1000, 1100 и 1200. Построить график зависимости коэффициента контактного трения от температуры полосы и материала валков. Решение. Для расчета коэффициента трения при установившемся процессе прокатки используем уравнение Экелунда-Бахтинова fуст = к1 к2 к3 (1,05 – 0,0005 Т). 1. Находим значения коэффициентов к1, к2, к3: - для стальных валков к1 = 1; - для чугунных валков к1 = 0,8; к2 = к3 = 1,30. 2. Рассчитываем коэффициент трения для каждой температуры: fч = к1 к2 к3 (1,05 – 0,0005 Т) = 0,8·0,64∙1,3(1,05 – 0,0005∙800) = 0,43; fc. = к1 к2 к3 (1,05 – 0,0005 Т) = 1 0,64∙1,3(1,05 – 0,0005∙800) = 0,54. Расчет коэффициента трения для других температур производится аналогично. Данные расчета сведены в табл. 5.2.
Таблица 5.2. При горячей прокатке
Кроме того, для определения сопротивления деформации целого ряда сталей и сплавов можно использовать регрессионные уравнения. В качестве примера в табл. 6.3 приведены уравнения, отвечающие условиям прокатки на толстолистовых станах: e = 0,02…0,20; U = 1…25 c-1; Т = 850…1200 0С. Данные, полученные с помощью этих уравнений, позволяют рассчитать истинный предел текучести, зависящий не только от каждого в отдельности трех основных параметров прокатки, но и от их совместного влияния. При расчете среднего контактного давления необходимо учитывать тот факт, что в случае плоской деформации (прокатка на листовых станах, когда уширение практически отсутствует) nx» 1,15. В том случае, когда деформация происходит в направлении всех трех главных осей (прокатка на блюмингах и слябингах), nx» 1. Таблица 6.3. Уравнения связи сопротивления деформации sS с термомеханическими параметрами при горячей прокатке
При прокатке блюмов, слябов, заготовок и толстых листов, а также тонких полос при малых степенях деформации (горячая прокатка), когда фактор формы при при 0,6 < при Если горячая прокатка полосы проводится с натяжением, когда фактор формы рср(нат) = рср где s0 и s1 - заднее и переднее натяжение полосы; pcp - среднее контактное давление без учета натяжения. Если величины переднего и заднего натяжения совпадают, то рср(нат) = рср При холодной прокатке тонкой полосы для определения величины среднего удельного давления можно использовать формулу А.И. Целиковым:
Значения hg, d, x0, x1, 2К0 , 2К1 вычисляются следующим образом:
где s0 и s1 - заднее и переднее натяжения;
При расчете контактной поверхности следует иметь в виду, что под действием усилия прокатки валок несколько сплющивается и поэтому фактический радиус валка Rcпл будет больше начального радиуса R0, т.е. Rcпл > R0. Тогда длину «сплющенной» дуги захвата определяют по формуле
где Величина т зависит только от механических свойств материала валков: - для стальных валков Е = 2,06×105 МПа; n = 0,; - для чугунных отбеленных валков Е = 1,26×105 МПа; n = 0,25. При холодной тонколистовой прокатке, когда абсолютные обжатия меньше 1 мм, а отношение усилия прокатки на единицу ширины полосы Момент прокатки Мпр определяется для правильного выбора двигателя и параметров оборудования клети. Существует несколько методов определения момента прокатки. Однако наибольшее распространение получили формулы, в которых крутящий момент определяют по усилию прокатки. Мпр = F аF, где аF - плечо равнодействующей сил на контактной поверхности, т.е. силы F, относительно линии центров валков. Плечо аF принято определять в долях длины очага деформации, т.е. аF = y lд . Величину y называют коэффициентом плеча момента прокатки. Таким образом, для двух рабочих валков имеем
Если считать, что усилие прокатки F = рср lд b (или контактное давление рср) задано, то основная проблема расчета крутящего момента сводится к правильному определению точки приложения силы F, т.е. к нахождению коэффициента плеча момента прокатки y. При практических расчетах для определения y используют эмпирические зависимости. Наиболее известными зависимостями такого вида являются уравнения, которые получили В. М. Луговской для условий прокатки толстой полосы y = 0,68 + 0,0018 e - 0,31 и М. И. Бояршинов для условий прокатки тонких полос y = 0,4566 – 0,021 где e - относительное обжатие, %. При наличии заднего F0 или переднего F1 усилия натяжения (или подпора) равнодействующая всех сил в очаге деформации отклоняется от вертикального направления; соответственно изменяется её плечо относительно центра валка. Положение равнодействующей в каждом конкретном случае можно определить из условия равновесия всех продольных сил, приложенных к полосе. Тогда величина крутящего момента может быть найдена по следующим зависимостям: - при прокатке с задним натяжением – Мпр = 2F y ld + F0 R.; - при прокатке с передним натяжением – Мпр =2 F y ld - F1 R. Если силы натяжения приложены к обоим концам полосы – переднему и заднему, то формула крутящего момента принимает вид
В частном случае, когда F0 = F1, т.е. равнодействующая F направлена вертикально и формула (6.5) совпадает с формулой крутящего момента (6.4) для свободной прокатки. Однако под воздействием сил F0 и F1 снижается величина равнодействующей F, а, следовательно, уменьшается крутящий момент. На рис. 6.1. и 6.2. представлены блок-схемы алгоритма расчета усилия и крутящего момента применительно к условиям прокатки на станах горячей и холодной прокатки.
нет
да
да нет
Рис. 6.1. Блок-схема расчета усилия и момента при горячей прокатке с учетом «сплющивания» валков и натяжения полосы
Рис. 6.2. Блок-схема расчета усилия при холодной прокатке с учетом «сплющивания» валков и натяжения полосы Примеры расчета
Пример 1. Построить кривые деформационного упроч
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.229 (0.014 с.) |

 .
.

 .
.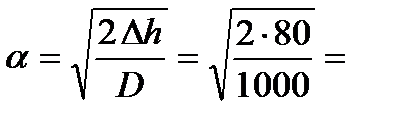 0,400 рад. = 22,9 град.
0,400 рад. = 22,9 град. , находим абсолютное обжатие для чугунных и стальных валков
, находим абсолютное обжатие для чугунных и стальных валков 720 мм.
720 мм. 245 мм.
245 мм. 0,327 рад.
0,327 рад. » 2160 мм.
» 2160 мм. 815 × 232,38 = 189400 мм2 = 0,1894 м2.
815 × 232,38 = 189400 мм2 = 0,1894 м2.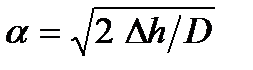 , определяем диаметр стальных и чугунных рабочих валков
, определяем диаметр стальных и чугунных рабочих валков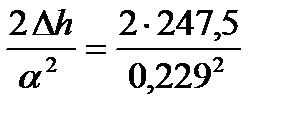 = 9439 мм» 9,44 м;
= 9439 мм» 9,44 м; = 34955 мм» 35 м.
= 34955 мм» 35 м. = 13 мм.
= 13 мм. 26 мм.
26 мм. 53,7 мм.
53,7 мм. 0,112.
0,112. 1,547 м = 1547 мм.
1,547 м = 1547 мм. 155 мм.
155 мм.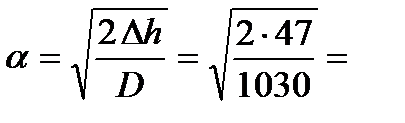 0,302 рад.
0,302 рад. = 980×155,58 = 152800 мм2 = 0,1528 м2.
= 980×155,58 = 152800 мм2 = 0,1528 м2. 1660 мм.
1660 мм. 1,5.
1,5. 9,24 м/с.
9,24 м/с.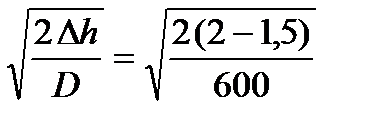 = 0,0577 рад = 3,31 град
= 0,0577 рад = 3,31 град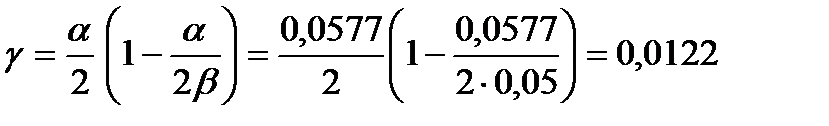 рад = 0,699 град.
рад = 0,699 град. = 1,5%.
= 1,5%. = 23,7%.
= 23,7%.
 0,2828 рад.
0,2828 рад. 0,0724 рад.
0,0724 рад. = 0,0049.
= 0,0049. мм.
мм. м/с.
м/с. м/с.
м/с. 1,38 м/с.
1,38 м/с. м/с.
м/с. = 98400000 /0,91 = 108100000 мм3/с.
= 98400000 /0,91 = 108100000 мм3/с.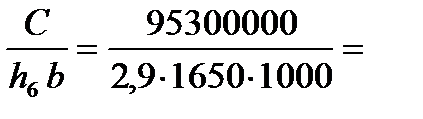 19,91 м/с; v5 =
19,91 м/с; v5 =  16,04 м/с;
16,04 м/с; 12,03 м/с; v3 =
12,03 м/с; v3 =  8,25 м/с;
8,25 м/с; 5,55 м/с; v1 =
5,55 м/с; v1 =  3,65 м/с.
3,65 м/с.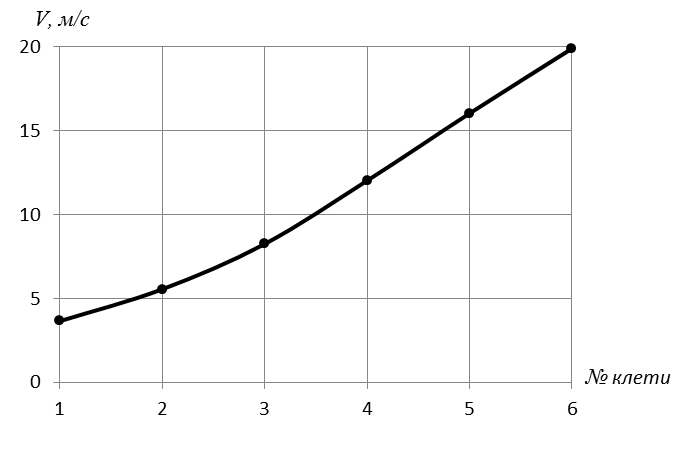
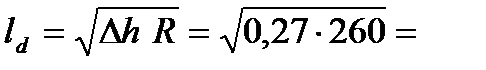 8,38 мм.
8,38 мм. =
=  3,10;
3,10; = 1, так как s0 = 0;
= 1, так как s0 = 0; 0,957; x12 =
0,957; x12 =  0,913;
0,913; 0,870; x14 =
0,870; x14 =  0,826.
0,826. 0,056;
0,056; 0,064;
0,064; 0,072;
0,072; 0,081.
0,081. . Тогда
. Тогда = 1102 мм» 1,1 м.
= 1102 мм» 1,1 м.
 . Проверяем данное неравенство на его соответствие объемной схеме деформирования
. Проверяем данное неравенство на его соответствие объемной схеме деформирования или 1,2 £ 2,17.
или 1,2 £ 2,17. =
=  = 0,4.
= 0,4. = 109,54 мм.
= 109,54 мм. = 0,05.
= 0,05.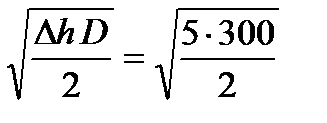 = 27,39 мм.
= 27,39 мм.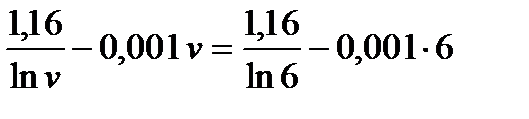 = 0,64;
= 0,64; < 1, т. е. при коротком очаге деформации, существенное влияние на величину среднего контактного давления оказывают внеконтактные, в том числе глубинные зоны очага деформации, не охваченные пластической деформацией. Поэтому коэффициент напряженного состояния ns определяется по следующим соотношениям:
< 1, т. е. при коротком очаге деформации, существенное влияние на величину среднего контактного давления оказывают внеконтактные, в том числе глубинные зоны очага деформации, не охваченные пластической деформацией. Поэтому коэффициент напряженного состояния ns определяется по следующим соотношениям: ;
; ,
, .
.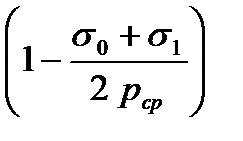

 .
. ;
;  ;
;  ,
, ;
;  - пределы текучести на входе в зону и выходе из зоны деформации при плоско- деформированном состоянии полосы; толщина полосы в нейтральном сечении
- пределы текучести на входе в зону и выходе из зоны деформации при плоско- деформированном состоянии полосы; толщина полосы в нейтральном сечении .
.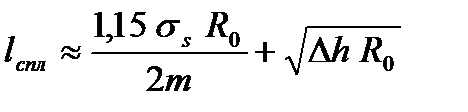 ,
, - модуль контактной жесткости валка; Е - модуль упругости материала валка; n - коэффициент Пуассона материала валка.
- модуль контактной жесткости валка; Е - модуль упругости материала валка; n - коэффициент Пуассона материала валка. > 8000 Н/мм, учет сплющивания валков обязателен.
> 8000 Н/мм, учет сплющивания валков обязателен. . (6.4)
. (6.4) при
при  ≤ 1,
≤ 1, . (6.5)
. (6.5)


