
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потери тепла в котельном агрегате
4 Контрольные вопросы 1. Общая классификация плановых показателей. 2. Классификация плановых показателей по экономической природе. 3. Что характеризует коэффициент корреляции? 4. Какая зависимость называется корреляционной? 5. Что называется эмпирической функцией регрессии? 6. Как определяются выборочные средние значения? Практическое занятие №4 Линейное программирование. Транспортная задача
Цель работы - ознакомиться с применением транспортных задач в сфере энергосбережения; составить оптимальный план перевозок. Работа выполняется в течение 2-х академических часов. Теоретическая часть Пусть имеется m пунктов отправления A1,A2,…,Am в которых сосредоточено или производится a1,a2,…,am единиц однородного товара. Необходимо доставить в каждый из n пунктов назначения B1,B2,…,Bn товар в количествах b1,b2,…,bn единиц. Известны также стоимости cij перевозок единицы товара из i - го пункта отправления в j -ый пункт назначения. Необходимо составить план перевозок, имеющий минимальную стоимость и позволяющий вывезти все грузы, полностью удовлетворив потребности. Запишем математическую модель транспортной задачи. Обозначим через Xij (i = 1,2,…,m) количество единиц груза, запланированных к перевозке от i-го поставщика к j-тому потребителю. Тогда условие задачи можно записать в виде таблицы 11. Стоимость всех перевозок выразится линейной формой
все грузы должны быть вывезены (эти уравнения получаются при суммировании элементов матрицы планирования по строкам),
потребности должны быть удовлетворены (уравнения получаются при суммировании по столбцам),
Таблица 11 Матрица планирования
Таким образом, требуется среди множества решений систем (15), (16) найти такое неотрицательное решение, которое минимизирует функцию (14). Известно, что задача всегда имеет решение, если выполняется условие баланса
Такая транспортная задача называется закрытой, в отличие от открытой, когда вместо некоторых уравнений в системе ограничений (15)-(16) присутствуют неравенства. Открытую модель необходимо преобразовать в закрытую, что всегда можно сделать. Так, если
Все тарифы на доставку груза в этот пункт полагаются равными нулю. Если же . Тарифы на доставку грузов от этого фиктивного поставщика полагают равными нулю. Тогда выполняется условие баланса и задача имеет решение.
Пример решения Имеются четыре леспромхоза А1, А2, А3,А4, в которых сосредоточено а1, а2, а3, а4 единиц пиломатериалов: а1 =300 ед., а2 = 400 ед., а3= = 300 ед., а4 = 400 ед. Необходимо доставить в каждый из четырех лесопильных заводов В1, В2, В3, В4 пиломатериалы в количестве b1, b2, b3, b4: b1= 200 ед., b2= 350 ед., b3= 400 ед., b4= 450 ед. Матрица стоимости перевозок имеет вид:
Составить оптимальный план перевозок, чтобы весь товар был вывезен, все потребности были удовлетворены и чтобы транспортные затраты были минимальными.
Решение 1. Выделим ячейки таблицы, которые будут играть роль оптимизирующих переменных (рис. 12). В нашем случае это ячейки «B3:E6» (размерность задачи 4 В ячейки «F3:F6» и «B7:E7» вводятся ограничения задачи − возможности поставщиков и потребности потребителей соответственно.
Рис. 12 – Исходные данные задачи
2. Проверим, что условие баланса выполнено, т.е. суммарные запасы равны суммарным потребностям. Для этого в ячейке «F7» найдем сумму по ячейкам «F3:F6» и «B7:E7» соответственно. Для ввода формулы суммирования, например в ячейку «F7», необходимо сделать эту ячейку текущей, затем выбрать в панели инструментов пиктограмму суммирования и выделить курсором в таблице блок ячеек, который необходимо просуммировать (в данном случае это блок ячеек «F3:F6»). Для завершения ввода формулы суммирования можно нажать клавишу Enter или еще раз выбрать в панели инструментов пиктограмму суммирования. Будем рассматривать решение задачи закрытого типа. Приведение задачи открытого типа к задаче закрытого типа известно из теории. 3. В ячейки «G3:G6» и «B8:E8» введем формулы суммирования по строкам и столбцам обведенной в рамку таблицы, обеспечивающие контроль выполнения заданных ограничений (в результате решения задачи значения соответствующих ячеек столбцов «F» и «G», а также строк 7 и 8 должны сравняться). Сначала формулу суммирования наберем в крайней ячейке (например «G3»), а затем размножим во все остальные ячейки «G4:G6». Убедившись, что активной является ячейка с введенной формулой, наведите курсор на правый нижний угол рамки ячейки (он примет форму +), нажмите левую кнопку мыши и растяните блок до ячейки «G6» включительно, после чего кнопку отпустите. 4. Ниже выделим (и также для наглядности обведем в рамку) еще две таблицы. В первую запишем стоимости перевозок, приведенные в условии задачи (блок ячеек «B12:E15»). Вторая таблица является вспомогательной для вычисления целевой функции (критерия) оптимизации (блок ячеек «B17:E20»). Для заполнения этой таблицы используется следующий прием. В ячейку «B17» записывается формула =B3*B12. Затем формула размножается на всю таблицу сначала по столбцу, а затем сразу по всем строкам. 5. Последним шагом выберем ячейку, в которую запишется целевая формула. В данном случае выберем ячейку «G12». В нее записывается формула суммирования ячеек «B17:E20». 6. После ввода всех данных и зависимостей вызовите Данные → Поиск решения. В появившейся панели Поиска решения (рис.13) необходимо: · указать целевую ячейку «G12»; · указать, что целевая ячейка минимизируется; · указать изменяемые ячейки «B3:E6»; · задать следующие о граничения: «B7:E7=B8:E8»; «F3:F6=G3:G6»; «B3:E6» целое; «B3:E6≥0»; · вызвать панель Параметры и установить курсором флажок Линейная модель, ОК. · выбрать пункт Выполнить. Решение задачи появится в ячейках «В3:Е8», которые были выделены в качестве оптимизируемых переменных. В ячейке «G12» появится значение суммарной стоимости перевозок, причем это значение будет минимальным из возможных (рис. 14).
Рис.13 – Окно поиска решения
Рис.14 – Решение задачи
3 Индивидуальные задания
Четыре леспромхоза заготавливают дрова в объемах: а1 =300N м3., а2 = 400 N м3, а3 = 300 N м3, а4 = 400 N м3. Эти дрова используют четыре котельных в объемах: b1 = 200N м3, b2 = 350N м3, b3 = 400N м3, b4 = 450N м3 (N – номер варианта). Матрица стоимости перевозок имеет вид:
Составить оптимальный план перевозок, чтобы все пиломатериалы были вывезены, все потребности были удовлетворены и чтобы транспортные затраты были минимальными.
4 Контрольные вопросы 1. Сформулируйте транспортную задачу.
2. Какие модели транспортной задачи Вы знаете? 3. Как сводится открытая модель к закрытой? 4. Какие основные этапы решения транспортной задачи? 5. В каком случае в математическую модель транспортной задачи вводится фиктивный пункт назначения. 6. В каком случае в математическую модель транспортной задачи вводится фиктивный пункт отправления. Практическое занятие №5 Линейное программирование. Задачи оптимизации в энергетическом планировании
Цель работы - ознакомиться с решением задач оптимизации; минимизировать энергозатраты на технологическую операцию. Работа выполняется в течение 2-х академических часов. Теоретическая часть
Для решения задачи планирования производственной программы необходимо основываться на оптимальных режимах работы оборудования. Под оптимальным понимается такое распределение нагрузки между параллельно работающими генерирующими источниками, при котором обеспечивается минимальный расход энергоресурсов на выработку требуемого количества энергии. В зависимости от постановки задачи оптимизации энергоресурсами могут быть расходы электроэнергии, топлива, тепла, водных ресурсов. Оптимизация может проводиться также и в целях минимизации затрат на энергоресурсы за счет оптимальной организации технологического процесса. Для решения данных задач используются методы математического моделирования. Экономико-математическая модель задачи оптимизации технологического процесса включает в себя следующие элементы: целевую функцию
уравнения ограничений
где В матричной форме задача имеет вид
где
x называется вектором-переменной, b − вектор ограничений, c − вектор стоимости, Aj – векторы условий, A – матрица условий, символ Изменив знак целевой функции (20) на max можно перейти к задаче на min и наоборот. Пример решения На предприятии имеются бревна длиной 6 м, которые необходимо разрезать на заготовки длиной 2,8 м в количестве 800 шт., 2,1 м − 900 шт., 1,8 м − 6000 шт. Необходимо составить оптимальный план раскроя материала, который обеспечивает минимальные отходы и тем самым энергозатраты, при условии выполнения плана по выходу заготовок. Решение Задачу можно решить с использованием симплекс-метода, реализуемого в Excel с помощью надстройки Поиск решения (вызывается из меню Данные).
На основании известных данных задачи: видов заготовок, которые должны быть получены, и их требуемого числа, составим варианты раскроя, обеспечивающие получение этих заготовок. Введем исходные данные в первые два столбца таблицы. Заготовим строки для решения и номеров вариантов раскроя. В нижней строке запишем формулы для подсчета отходов. Для этого введем в ячейку «С8» формулу =$E$1-(C5*$A5+C6*$A6+C7*$A7) и скопируем ее далее в этой строке по предполагаемому числу вариантов. При правильном вводе формулы во всей строке будут числа 6. Раскрой начнем с самой длинной заготовки: в ячейку «С5» вводим 2 (из бревна длиной 6 м можно получить две заготовки длиной 2,8 м). Из отходов, которые автоматически считаются в ячейке «С8», нельзя больше получить средние и маленькие заготовки, поэтому в ячейки «С6» и «С7» вводим 0. Переход к следующему варианту раскроя осуществляется по правилу: последовательно уменьшаем число средних заготовок до 0 и из оставшихся выкраиваем маленькие заготовки, после чего уменьшаем число больших заготовок на 1, вновь повторяем процедуру уменьшения числа средних заготовок и так поступаем до тех пор, пока не останутся только маленькие заготовки. Пример раскроя представлен на рис.15. Обозначим через
При этом должны выполняться условия выполнения плана по количеству заготовок, т. е.
По смыслу задачи
Таким образом, для решения поставленной задачи необходимо найти
Рис.15 – Варианты раскроя
Подготовим область для подсчета числа выкраиваемых заготовок и суммарного объема отходов. Введем в ячейку «C10» формулу =C5*C$2 и скопируем ее в диапазон ячеек «C10:H13». Слева, в колонку В, введем суммы для подсчета числа полученных заготовок и общего объема отходов. В ячейку «B10» запишем формулу =СУММ(С10:H10) и скопируем ее в область «B11:B13». При правильном вводе формулы в ячейках «B10:H13» появятся 0. Таким образом, необходимо определить оптимальный план раскроя (ячейки «C2:H2») при ограничениях: решение неотрицательное и целое, число получаемых заготовок (ячейки «B10:B12») равно заданному числу заготовок (ячейки «В5:В7»), и при этом минимизировать суммарный объём отходов (ячейка «В13»). Выполним программу Поиск решения. В меню Данные активизируем команду Поиск решения. В окне Установить целевую ячейку укажем ячейку «В13», содержащую модель.
Поскольку необходимо минимизировать суммарный объем отходов, то активизируем кнопку Минимальному значению. Изменяя ячейки – «C2:H2». Используя кнопку Добавить, опишем ограничения задачи. Окончательный вид окна Поиск решения представлен на рис.16.
Рис.16 – Окно поиска решения Командой Параметры вызываем диалоговое окно и устанавливаем флажки: Линейная модель, Неотрицательные значения, Автоматическое масштабирование. Щелкнем на кнопке ОК, а затем – Выполнить. Решение приведено на рис.17. Вывод. По первому варианту нужно распилить 400 брёвен, по четвёртому − 450 брёвен, по шестому − 1850 брёвен. При этом отходы будут минимальными и равными:
Рис. 17 – Решение 3 Индивидуальные задания
На деревообрабатывающем предприятии имеются брёвна длиной L м, которые необходимо разрезать на доски длиной l1,l2,l3 м в количестве p1,p2,p3 соответственно. Необходимо минимизировать энергозатраты на раскряжевку бревен путем разработки оптимального плана раскройки бревен, который обеспечивает минимальные отходы, при условии выполнения плана по выходу заготовок. Исходные данные приведены в таблице 12. Таблица 12 Исходные данные
4 Контрольные вопросы 1. Сформулируйте задачу линейного программирования. 2. Что представляет собой целевая функция. 3. Что представляют собой уравнения ограничения. 4. Приведите матричную форму задачи оптимизации. 5. Как осуществить переход от задачи на max к задаче на min.
Лабораторная работа №1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.24 (0.082 с.) |




 , (14)
, (14) , (15)
, (15) ,
, 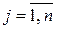 . (16)
. (16)

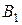




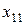


















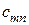

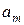


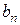

 . (17)
. (17) , то в математическую модель транспортной задачи вводится фиктивный (n+1) -й пункт назначения Bn+1 с потребностями в грузе в количестве
, то в математическую модель транспортной задачи вводится фиктивный (n+1) -й пункт назначения Bn+1 с потребностями в грузе в количестве (18)
(18) , то в математическую модель транспортной задачи вводится фиктивный (m+1)- й пункт отправления Am+1, которому приписывается запас груза, равный
, то в математическую модель транспортной задачи вводится фиктивный (m+1)- й пункт отправления Am+1, которому приписывается запас груза, равный (19)
(19)
 4). Их удобно для наглядности обвести в рамку или выделить цветом. Для этого установите курсор в ячейку «В3», нажмите левую кнопку мыши и, удерживая ее, растяните блок до ячейки «Е6», после чего кнопку отпустите. Теперь в панели инструментов выберите мышкой стрелку вниз рядом с пиктограммой рисования рамок и в появившемся списке выберите рамку по контуру блока ячеек. Аналогично можно выделить цветом. Кроме того, в ячейки «A1:F2» и «A1:A7» полезно ввести названия строк и столбцов таблицы.
4). Их удобно для наглядности обвести в рамку или выделить цветом. Для этого установите курсор в ячейку «В3», нажмите левую кнопку мыши и, удерживая ее, растяните блок до ячейки «Е6», после чего кнопку отпустите. Теперь в панели инструментов выберите мышкой стрелку вниз рядом с пиктограммой рисования рамок и в появившемся списке выберите рамку по контуру блока ячеек. Аналогично можно выделить цветом. Кроме того, в ячейки «A1:F2» и «A1:A7» полезно ввести названия строк и столбцов таблицы.



 (20)
(20) (21)
(21) , (22)
, (22) постоянные числа. Запись
постоянные числа. Запись  означает, что
означает, что  .
. , (23)
, (23) , (24)
, (24) , (25)
, (25) ,
,  ,
,  ,
,  ,
,  ,
, .
. означает транспонирование.
означает транспонирование.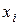 количество бревен, разрезанных по i -му варианту (i = 1,2,…,6). Тогда суммарный остаток отходов запишется в виде линейной функции
количество бревен, разрезанных по i -му варианту (i = 1,2,…,6). Тогда суммарный остаток отходов запишется в виде линейной функции (26)
(26) (27)
(27) − целочисленные и
− целочисленные и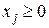 (
( ). (28)
). (28) при ограничениях (27) – (28).
при ограничениях (27) – (28).
 м.
м.



