
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальности 1-43 01 06 «Энергоэффективные технологии и энергетический менеджмент»Содержание книги
Поиск на нашем сайте
Специальности 1-43 01 06 «Энергоэффективные технологии и энергетический менеджмент»
Минск 2013 УДК 658.26(076.5)+658.14/.17:620.9(076.5) ББК 31.19я73 М54
Рассмотрены и рекомендованы к изданию редакционно-издательским советом университета.
Рецензент: заведующий кафедрой МиЭП БГТУ, доктор экономических наук, профессор А. В. Неверов
Энергетическое планирование и финансы в сфере энергосбережения: методические указания к практическим занятиям и лабораторным работам для студентов специальности 1-43 01 06 «Энергоэффективные технологии и энергетический менеджмент» / сост. А.С. Дмитриченко, С.А. Манжинский – Минск: БГТУ, 2013. – 75 с.
Представленные материалы являются частью учебно-методического комплекса «Энергетическое планирование и финансы в сфере энергосбережения», разработанного в соответствии с типовой учебной программой для студентов специальности 1-43 01 06 «Энергоэффективные технологии и энергетический менеджмент». Практические занятия и лабораторные работы направлены на формирование у студентов практических навыков решения прикладных задач по прогнозированию и планированию в сферах энергосбережения и инвестиционному проектированию, а также в области организации и управления производственно-хозяйственной деятельностью предприятий.
УДК 658.26(076.5)+658.14/.17:620.9(076.5) ББК 31.19я73 © УО «Белорусский государственный Введение Для решения задач организации и управления производственно- хозяйственной деятельностью предприятий, создания и внедрения новых технологий будущему инженеру-энергоменеджеру необходимо иметь не только технические, но и экономические знания. Экономические знания, которые получают студенты, должны: – основываться на научных концепциях, принятых в настоящее время в экономической науке; – соответствовать реально действующим в энергетической отрасли хозяйственным отношениям; – носить базовый характер и развивать у студентов навыки и умения для дальнейшего их развития в процессе практической деятельности. Содержание методических указаний сформировано в контексте этих требований и является логическим продолжением курса «энергетическое планирование и финансы в сфере энергосбережения». Практические занятия и лабораторные работы, как в теоретическом, так и в методическом плане рассмотрены с учетом специфики электроэнергетической отрасли и промышленной энергетики.
Важную роль в обеспечении эффективного развития предприятия играет принятие экономически обоснованных решений по реализации инвестиционных проектов. Составной частью всех выполняемых и готовящихся к выполнению инвестиционных проектов являются вопросы энергоэффективности. В методических указаний приводятся лабораторные работы, выполняемые в MS Excel, по расчету показателей финансово-экономической эффективности инвестиционных проектов. Целью настоящего издания является закрепление у студентов теоретических знаний по дисциплине и формирование практических навыков решения прикладных задач в области планирования производственно-хозяйственной деятельностью предприятий, а также принятия управленческих решений в сфере реализации инвестиционных проектов. Издание содержит тематику лекций, практические и лабораторные занятия, методические указания, контрольные вопросы и задания, соответствующие основным темам дисциплины «Энергетическое планирование и финансы в сфере энергосбережения» специальности 1-43 01 06 «Энергоэффективные технологии и энергетический менеджмент». Практическое занятие №1 Планирование производственно-хозяйственной Деятельности предприятия Цель работы - ознакомиться с различными методами планирования; разработать перспективный план выработки электроэнергии страны. Работа выполняется в течение 2-х академических часов.
Теоретическая часть
В практике управления производственно-хозяйственной деятельностью предприятий используются различные методы планирования: • балансовый; • расчетно-аналитический; • экономико-математического моделирования; • программно-целевой; • графоаналитический. Балансовый метод планирования обеспечивает установление связей между потребностями в ресурсах и источниках их покрытия, а также между разделами плана. Например, балансовый метод увязывает производственную программу с производственной мощностью предприятия, трудоемкость производственной программы с численностью работающих. На предприятии составляются балансы производственной мощности, рабочего времени, материальный, энергетический, финансовый и др.
Расчетно-аналитический метод используется для расчета показателей плана, анализа их динамики и факторов, обеспечивающих необходимый количественный уровень показателей. В рамках этого метода определяется базисный уровень основных показателей плана и их изменения в плановом периоде за счет влияния основных факторов, рассчитываются индексы изменения плановых показателей по сравнению с базисным уровнем. Метод экономико-математического моделирования применяют для разработки экономических моделей, отражающих зависимость количественных параметров (показателей) от влияния основных факторов, альтернативных вариантов плана и выбора оптимального. Программно-целевые методы позволяют составлять план в виде программы, т.е. комплекса задач и мероприятий, объединенных одной целью и приуроченных к определенным срокам. На основе ранжирования целей (генеральная цель – стратегические и тактические цели) составляется граф типа «дерево целей» – исходная база для формирования системы показателей программы и оргструктуры управления ею. Графоаналитический метод дает возможность визуализации результатов экономического анализа графическими средствами. С помощью графиков выявляется количественная зависимость между сопряженными показателями. В данной работе рассмотрен графоаналитический метод планирования. При этом методе планирования сталкиваются со следующей задачей: в результате опыта получен ряд значений переменных
где а1, а2, …,аm –параметры, чтобы значения f(x, а1, а2, …,аm) в точках Одним из основных методов нахождения параметров эмпирической зависимости является метод наименьших квадратов. Этот метод не решает вопроса о выборе общего вида аналитической функции, а дает возможность при заданном типе аналитической функции подобрать наиболее вероятные значения для ее параметров. Если y зависит от x линейно y=ax+b, то эмпирическая зависимость определяется при помощи системы уравнений
Полученная система решается любым известным методом (Гаусса, Крамера, матричным) или с помощью стандартных программ на компьютере.
Пример решения Найти эмпирическую зависимость по данным, приведенным в таблице 1. Таблица 1 Эмпирические данные
Решение Нахождение эмпирических формул методом наименьших квадратов можно осуществлять в среде Excel, используя: · функции СТЕПЕНЬ, ПРОИЗВЕД, СУММ, СУММКВ, СУММПРОИЗВ, · формулы массива МОБР, МУМНОЖ, · графический анализ с помощью линий тренда. Рассмотрим на конкретных примерах, как работают эти функции (рис.1). 1. Внесем данные задачи в ячейки «B4:B13» и «C4:C13». 2. Вычислим xi2, введя в ячейку «D4» формулу «=B4*B4» и затем скопировав ее в ячейки «D5:D13» (направив указатель мыши на черный квадрат в правом нижнем углу ячейки, чтобы он принял вид черного крестика, и протащив в ячейку D6 и т.д.). Аналогично найдем произведения xi yi и результат запишем в ячейках «E4:E13». Эти же результаты можно получить, используя функции СТЕПЕНЬ и ПРОИЗВЕД в категории Математические Мастера функций.
3. Найдем сумму значений в ячейках «B4:B13» и результат запишем в ячейку «B14». Для этого выделим соответствующие ячейки и нажмем пиктограмму суммирование на Панели инструментов. Для суммирования элементов массива можно воспользоваться функциями СУММ, СУММКВ, СУММПРОИЗВ в категории Математические Мастера функций. 4. Система (2) для нашего примера примет вид:
Обозначим Систему решим матричным методом по формуле:
Рис.1 – Пример решения
· В ячейках «L3:M4» запишем матрицу А. · Найдем обратную матрицу
Зададим адреса матрицы А «L3:M4» и нажмем Ctrl+Shift+Enter для выполнения действия. · В ячейках «M9:M10» запишем столбец свободных членов B. · Умножим матрицу · Вызовем формулу массива
Ctrl+Shift+Enter для выполнения действия. Таким образом, искомая эмпирическая функция имеет вид 4. Построим точечную диаграмму, используя Мастер диаграмм, который вызывается с помощью команды Вставка → Диаграмма или при нажатии соответствующей кнопки на панели инструментов. · Выделим данные, которые будут включены в диаграмму, т.е. ячейки «B4:C13». · Выберем команду Вставка → Диаграмма (можно щелкнуть кнопку Мастер диаграмм на панели инструментов). · На первом шаге работы Мастера диаграмм выберем Тип диаграммы вариант Точечная и щелкнем Далее. · Можно пропустить остальные шаги и сразу нажать кнопку Готово. На экране появится встроенный график. При необходимости его можно перетащить в более удобное место, зацепив мышью за край области диаграммы. · Добавим к исходной точечной диаграмме линию тренда. Для этого используем команду меню Диаграмма → Добавить линию тренда, которая появляется, если диаграмма выделена. · В окне Линия тренда во вкладке Тип и выберем шаблон кривой. В нашем случае Линейная
3 Индивидуальные задания
Выработка электроэнергии в стране для различных вариантов заданий N в течение 10 лет приведена в таблице 2. Графоаналитическим методом планирования определить план выработки на следующий год.
Таблица 2 Выработка электроэнергии
4 Контрольные вопросы 1. Определение энергетического планирования. 2. Балансовый метод энергетического планирования. 3. Расчетно-аналитический метод энергетического планирования. 4. Метод экономико-математического моделирования. 5. Программно-целевой метод энергетического планирования. 6. Графоаналитический метод энергетического планирования. Практическое занятие №2 Теоретическая часть
Основным показателем энергетической экономичности агрегата (процесса) является его коэффициент полезного действия, равный отношению полезной нагрузки к подведенной мощности:
Отношение потерь мощности в агрегате к подведенной мощности называется величиной удельных потерь мощности в агрегате.
Из выражений (3) и (4) следует, что сумма этих двух показателей энергетической эффективности агрегата равна 100%:
где Э – общее количество энергии; П — количество выпущенной агрегатом продукции в течении рассматриваемого промежутка времени. При постоянной нагрузке (производительности агрегата)
Основой энергетического нормирования являются энергетические характеристики агрегатов — зависимости энергетической мощности, затрачиваемой на технологический процесс или теряемой в агрегате, от величины выпуска основной продукции агрегатом в единицу времени. Соответственно различают основные энергетические характеристики: подведенной мощности Р=f1(Пчас); полезной мощности Рпол=f2(Пчас); потерь в агрегате Рпот=f3(Пчас) (рис.2). Наибольшее значение в энергоэкономических расчетах имеет энергетическая характеристика подведенной мощности, которая обычно называется расходной характеристикой агрегата. Отрезок оси ординат, отсекаемый расходной характеристикой в точке а, характеризует величину потерь холостого хода.
1 – подведенная мощность; 2 – полезная мощность; 3 – потери в агрегате Рис.2 – Энергетические характеристики агрегатов
По основным характеристикам могут быть построены производные (вторичные) характеристики показателей энергетической экономичности агрегата (рис.3): к. п. д. aгрегата η = f 4 (Пчас), удельного расхода энергии на единицу продукции Эп = f5 (Пчас), удельных потерь в агрегате pуд = f6 (Пчас).
1 –к.п.д. агрегата; 2 – удельный расход энергии; 3 – удельные потери Рис.3 – Производные характеристики показателей энергетической экономичности агрегата
Энергетические характеристики агрегатов, как правило, представляют нелинейные зависимости. В этом случае для получения эмпирических зависимостей применяют метод выравнивания, суть которого состоит в следующем.
Пусть в результате опыта получен ряд значений переменных x и y. Причем для переменных x и y их соответствующие значения xi, yi, i=1…n, таковы, что точки Mi (xi, yi), не располагаются на прямой линии. И пусть геометрическим или каким-либо другим образом определен вид нелинейной зависимости y от x. Найдем, если можно, взаимно-однозначное преобразование X=φ(x, y), Y=ψ(x,y), при котором эта нелинейная зависимость переходит в линейную Y=aX+b. По формулам X=φ(x, y), Y=ψ(x,y) и исходным данным найдем соответствующие значения новых переменных X и Y. При этом точки Mi (Xi, Yi), i=1…n, будут располагаться вблизи некоторой прямой. По новым данным методом наименьших квадратов найдем эмпирическую зависимость Y=aX+b. Затем, переходя в этой формуле к исходным переменным x и y, найдем искомую зависимость y от x. В таблице 3 указаны преобразования, с помощью которых можно свести к линейной зависимости некоторые классы функций, наиболее часто встречающиеся на практике.
Таблица 3 Классы функций
На рис.4 − 7 приведены графики некоторых функциональных зависимостей.
Параметры  и и  линейной зависимости обычно ищут методом наименьших квадратов (см. практическое занятие №1). После чего находят параметры линейной зависимости обычно ищут методом наименьших квадратов (см. практическое занятие №1). После чего находят параметры 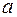 и и  и записывают первоначальную зависимость. и записывают первоначальную зависимость.
Рис.4 – Зависимость
Рис.5 – Зависимость 
Рис.6 – Зависимость 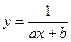
Рис. 7 – Зависимость 
Пример решения Найти эмпирическую зависимость по результатам испытаний, приведенных в таблице 4.
Таблица 4 Результаты испытаний
Решение Предположим, что зависимость задается формулой y=beax. Решим рассматриваемую задачу с помощью Мастера диаграмм. На основе диапазона данных построим точечную диаграмму и, используя средства форматирования, приведем ее к удобному для восприятия виду. На диаграмме выделим ряд значений и выбрав контекстное меню (нажатием правой клавиши мыши), выберем команду Добавить линию тренда. Будет открыто диалоговое окно Линия тренда, содержащее вкладку Тип, где задается вид тренда (уравнения): линейный, логарифмический, полиномиальный (от 2-й до 6-й степени включительно), степенной, экспоненциальный. Для того чтобы получить аналитическое выражение выбранного уравнения, необходимо на вкладке Параметры активизировать флажок Показывать уравнение на диаграмме. Если поставить флажок Поместить на диаграмму величину достоверности аппроксимации R^2, то в области построения будет выделено значение показателя Выбирая предлагаемые виды зависимости, убеждаемся, что экспоненциальная зависимость y=beax наиболее хорошо аппроксимирует эмпирические данные. Решим данную задачу методом выравнивания. Используя преобразование Y=lny X=x, найдем параметры линейной зависимости Y=lnb+aX. Сравним полученные решения (рис.8).
Рис. 8 – Пример решения 3 Индивидуальные задания Экспериментальные значения энергетических характеристик агрегата при различных величинах выпуска продукции в единицу времени в зависимости от номера варианта N приведены в таблице 5. Найти эмпирические зависимости Таблица 5 Практическое занятие №3 Система плановых показателей в энергетическом планировании
Цель работы - ознакомиться с основными плановыми показателями в энергетическом планировании; оценить степень тесноты связи между двумя энергетическими параметрами. Работа выполняется в течение 4-х академических часов. Теоретическая часть Система плановых показателей, единиц измерения и порядок их определения имеют важнейшее значение для планирования. Каждый показатель является моделью какого-либо экономического явления. Он должен наиболее полно отражать природу планируемых энергетических процессов, и при этом показатели не должны противоречить друг другу, должны быть взаимосвязаны с количественной и качественной стороны, и составлять как бы единое целое. Перечень показателей планов, единицы их измерения и точность расчета изменяются в зависимости от того ведется ли расчет плана для энергетической системы в целом, для отдельных электрических станций, предприятия сети или же других подразделений, а также на какой срок составляется такой план (год, месяц, сутки и т.д.). Показатели, применяемые в планировании делятся на несколько групп. По экономической природе различают: 1. Стоимостные показатели связаны с учетом в денежной форме затрат общественного труда на производство различных видов энергии. 2. Натуральные показатели выражают свойство потребительской стоимости, это количество, выработанной Гкал, кВт*ч или же потребленного условного топлива. Общая классификация плановых показателей: – качественные – являются обобщенными и характеризуют результаты какой-либо хозяйственной деятельности (прибыль, рентабельность, себестоимость ед. продукции, энергоемкость, энергоэффективность) или степень эффективности использования средств производства и рабочего времени (используемые мощности, нормы затрат топлива, электрической энергии, тепла и т.д.); – количественные - к оличественные показатели выражают численную меру экономического явления, например, количество, произведенное кВтч, ГДж, численность работников, число отремонтированных агрегатов и т.д. Все виды плановых показателей находятся в неразрывном единстве, поскольку характеризуют разные стороны взаимосвязанных экономических явлений. Для того, чтобы оценить степень тесноты связи между двумя экономическими явлениями выполняется корреляционный анализ. Корреляционный анализ исследует взаимосвязь случайных величин на основе экспериментальных данных. Предположим, что результаты эксперимента описываются двумя случайными величинами Для определения статистической зависимости данные наблюдений записывают в виде корреляционной таблицы 6, где
Здесь mij означает, что пара значений (xi,yi) наблюдалось mij раз, ni и mj соответствующие частоты наблюдаемых значений xi и yj, i=1,2,…,k; j=1,2,…,k.
Таблица 6 Корреляционная таблица
В случае, когда случайные величины являются непрерывными (т.е. могут принимать любое значение из соответствующих интервалов), составляется интервальная корреляционная таблица. Условным средним называют среднее арифметическое значений Y, соответствующих значению X=x. Например,
Корреляционной зависимостью Y от X называют зависимость:
Уравнение (8) называют эмпирическим уравнением регрессии Y на X; функцию f(x) Аналогично определяются условная средняя
Распределение системы (X,Y) характеризуется числовыми параметрами: математическими ожиданиями компонент mx, my; дисперсиями Здесь и дальше, будем считать, что двумерная случайная величина (X,Y) распределена нормально, тогда уравнения линейной регрессии Y на X и X на Y имеют вид:
По корреляционной таблице 6, найдем оценки параметров линейной регрессии:
Выборочный коэффициент корреляции Эмпирическая функция линейной регрессии Y на X и X на Y соответственно задаётся уравнениями
Замечание 1. Если построить на одном корреляционном поле две линии регрессии Y на X и X на Y, то они пересекутся в точке O Замечание 2. В случае, когда данные наблюдений X и Y записаны в виде интервальной корреляционной таблицы в формулах (10) – (13) вместо xi и yi обычно берут середины, соответствующих интервалов. Для проверки соответствия линейной регрессии результатам наблюдений вычисляется наблюдаемое значение критерия
и по таблице критических точек распределения Стьюдента (таблица 7) по заданному уровню значимости α и числу степеней свободы k = n–2, находится
Таблица 7 T-Распределение Стьюдента.
Если Пример решения Данные наблюдений случайных величин X и Y приведены в корреляционной таблице 8. Выполнить корреляционный анализ результатов эксперимента, описываемого случайными величинами. Решение Построим корреляционное поле (рис.9).
Таблица 8 Исходные данные
Рис.9 – Корреляционное поле Находим середины интервалов группировки статистических данных и записываем их в таблицу 9.
Таблица 9 Вспомогательная таблица
Определим корреляционный момент
Коэффициент корреляции будет Запишем эмпирические линейные функции регрессии Y на X и X на Y.
Отобразим эти прямые на рис. 10. Точка пересечения графиков имеет координаты Проверим соответствие линейной регрессии с результатами наблюдения
Рис.10– Графики линейных функций регрессий Для уровня значимости α = 0,05 при степени свободы ν = n–2=98 по таблице 7 находим Решение при помощи MS Excel представлено на рис. 11.
Рис.11 – Решение при помощи Excel
Так как tнабл > tтабл, то линейная модель зависи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.213.208 (0.014 с.) |

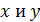 . Требуется получить такую эмпирическую зависимость
. Требуется получить такую эмпирическую зависимость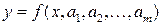 , (1)
, (1) , мало отличались от опытных данных yi,i=1…..n.
, мало отличались от опытных данных yi,i=1…..n. (2)
(2)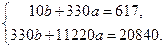
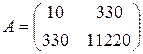 − матрица системы,
− матрица системы, 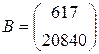 − столбец свободных членов,
− столбец свободных членов, 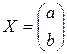 − столбец неизвестных.
− столбец неизвестных.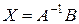 , выполнив действия, записанные ниже.
, выполнив действия, записанные ниже.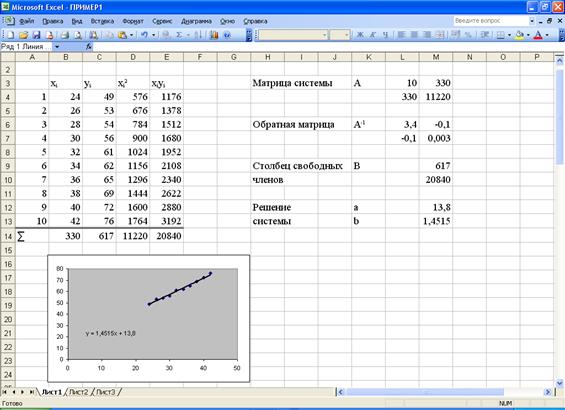
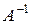 . Для этого выделим область соответствующего размера диапазон «L6:M7» для записи обратной матрицы. Вызовем формулу массива
. Для этого выделим область соответствующего размера диапазон «L6:M7» для записи обратной матрицы. Вызовем формулу массива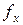 → Математические → МОБР → ОК.
→ Математические → МОБР → ОК.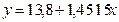 .
.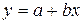 . Во вкладке Параметры поставим флажки: Показывать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации R2 и нажмем ОК. На диаграмме появится линия тренда и ее уравнение.
. Во вкладке Параметры поставим флажки: Показывать уравнение на диаграмме, поместить на диаграмму величину достоверности аппроксимации R2 и нажмем ОК. На диаграмме появится линия тренда и ее уравнение. (3)
(3)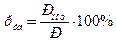 (4)
(4) (5) Третьим показателем энергетической экономичности процесса является удельный расход энергии на единицу основной продукции, выпускаемой агрегатом.
(5) Третьим показателем энергетической экономичности процесса является удельный расход энергии на единицу основной продукции, выпускаемой агрегатом. ед. энергии/ед. продукции, (6)
ед. энергии/ед. продукции, (6) (7)
(7)


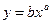
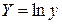 ;
; 
 ;
;
 ;
; 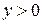

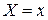
 ;
;  ;
; 

 ;
; 
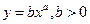



 , по которому можно судить, насколько хорошо выбранное уравнение аппроксимирует эмпирические данные. Чем ближе
, по которому можно судить, насколько хорошо выбранное уравнение аппроксимирует эмпирические данные. Чем ближе 
 Р=f1(Пчас); Рпол=f2(Пчас); Рпот=f3(Пчас), η = f 4 (Пчас), Эп = f5 (Пчас), p = f6 (Пчас). Определить величину потерь холостого хода.
Р=f1(Пчас); Рпол=f2(Пчас); Рпот=f3(Пчас), η = f 4 (Пчас), Эп = f5 (Пчас), p = f6 (Пчас). Определить величину потерь холостого хода. и
и 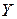 .
. ;
;  ;
;  .
.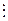
 .
.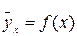 (8)
(8) называют эмпирической регрессией Y на X, а ее график - линией регрессии Y на X.
называют эмпирической регрессией Y на X, а ее график - линией регрессии Y на X. и корреляционная зависимость X от Y:
и корреляционная зависимость X от Y: (9)
(9) ,
,  ; корреляционным моментом (ковариацией)
; корреляционным моментом (ковариацией)  ; коэффициентом корреляции
; коэффициентом корреляции  ,
, 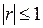 .
. и
и 
 ;
;  ; (10)
; (10) ; (11)
; (11) ; (12)
; (12) ; (13)
; (13) - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции. характеризует тесноту линейной связи между
характеризует тесноту линейной связи между  , то элементы выборки
, то элементы выборки 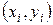 ,
, 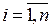 лежат на прямой линии, а
лежат на прямой линии, а  к 1, тем связь сильнее; чем ближе
к 1, тем связь сильнее; чем ближе 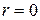 .
. ;
;  .
. , и угол между этими прямыми тем меньше, чем ближе коэффициент корреляции к
, и угол между этими прямыми тем меньше, чем ближе коэффициент корреляции к 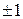 .
.
 . Затем сравнивается наблюдаемое значение критерия с табличным.
. Затем сравнивается наблюдаемое значение критерия с табличным. , то гипотеза о некоррелированности составляющих X и Y отвергается. Если же
, то гипотеза о некоррелированности составляющих X и Y отвергается. Если же  , то нет основания отвергать гипотезу о некоррелированности случайных величин X и Y.
, то нет основания отвергать гипотезу о некоррелированности случайных величин X и Y.




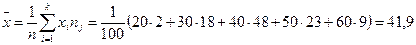 ;
;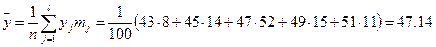

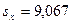 ;
;
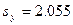 .
.
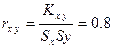 .
.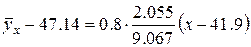 ;
;  ;
; ;
;  .
. , следовательно, вычисления выполнены правильно.
, следовательно, вычисления выполнены правильно.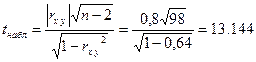

 .
.



