Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромеханические воздействия магнитного поля на проводники с током используются также в магнитоэлектрических измерительных приборах, применяемых в цепях постоянного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Б) Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда. Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
В) Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью
Сила Лоренца направлена перпендикулярно векторам Г) При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость
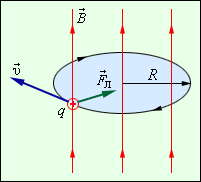
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 4.18.2).
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R. Угловая скорость движения заряженной частицы по круговой траектории
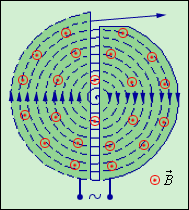
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 4.18.3.
9.а) Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества: где χ m называют магнитной восприимчивостью. В ферромагнитных материалах нет однозначной связи между M и H из-за магнитного гистерезиса. Магнитная индукция определяется через намагниченность как: б) Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле В’ в) Магнетики — материалы, вступающие во взаимодействие с магнитным полем, выражающееся в его изменении, а также в других физических явлениях — изменение физических размеров, температуры, проводимости, возникновению электрического потенциала и т. д. В этом смысле к магнетикам относятся практически все вещества (поскольку ни у какого из них магнитная восприимчивость не равна нулю точно), большинство из них относится к классам диамагнетиков (имеющие небольшую отрицательную магнитную восприимчивость — и несколько ослабляющие магнитное поле) или парамагнетиков (имеющие небольшую положительную магнитную восприимчивость — и несколько усиливающие магнитное поле); более редко встречаются ферромагнетики (имеющие большую положительную магнитную восприимчивость — и намного усиливающие магнитное поле), о еще более редких классах веществ по отношению к действию на них магнитного поля. Известно два различных механизма магнетизма:1)зонный магнетизм;2)молекулярный магнетизм.Выделяют несколько основных типов магнетиков, различимых по конфигурации их магнитных структур: 1)ферромагнетики,2)неколлинеарные ферромагнетики,3)антиферромагнетики,4)ферримагнетики,5)гелимагнетики, 6)спиновые стёкла. Г) Напряжённость магни́тного по́ля — (стандартное обозначение Н) это векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. В СИ:
10.а) Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током. Б) Согласно закону электромагнитной индукции Фарадея (в СИ):
В) Правило Ленца определяет направление индукционного тока и гласит:Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.Правило сформулировано в 1833 году Э. Х. Ленцем. Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока. Так, если изменение магнитного потока вызвано изменением площади контура (например, за счёт движения одной из сторон прямоугольного контура), то индукционный ток возбуждается силой Лоренца, действующей на электроны перемещаемого проводника в постоянном магнитном поле. Если же изменение магнитного потока связано с изменение величины внешнего магнитного поля, то индукционный ток возбуждается вихревым электрическим полем, появляющимся при изменении магнитного поля. Однако в обоих случаях индукционный ток направлен так, чтобы скомпенсировать изменение потока магнитного поля через контур. Если внешнее магнитное поле, пронизывающее неподвижный электрический контур, создаётся током, текущим в другом контуре, то индукционный ток может оказаться направлен как в том же направлении, что и внешний, так и в противоположном: это зависит от того, уменьшается или увеличивается внешний ток. Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному. В обратном случае, когда внешний ток уменьшается со временем, уменьшение магнитного потока приводит к возбуждению индукционного тока, стремящегося увеличить поток, и этот ток направлен в ту же сторону, что и внешний ток.. Г)Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре[1] при изменении тока, протекающего по контуру.При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока
Коэффициент пропорциональности Д) Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, имагнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4]. В формуле Е) Вокруг контура, по которому проходит электрический ток, всегда существует магнитное поле, причем магнитное поле возникает и исчезает вместе с возникновением и исчезновением тока. Следовательно, часть энергии тока идет на создание магнитного поля, которое, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. Она равна работе против ЭДС самоиндукции, возникающей при замыкании цепи. Определим эту работу. Подключим к источнику тока проводящий контур с индуктивностью L. При замыкании цепи за время Δt сила тока увеличится от нуля до некоторого значения I. При этом магнитный поток, создаваемый этим током, возрастет от нуля до значения При переносе заряда q источник тока совершает работу
Работа, совершаемая источником тока против ЭДС самоиндукции, и будет равна энергии W магнитного поля:
Если магнитное поле создано током, проходящим в соленоиде, то
Так как Согласно теории близкодействия, энергия магнитного поля (как и энергия электрического поля) распределена по всему объему V пространства, в котором существует магнитное поле. Величина
где В — модуль индукции магнитного поля, μ — магнитная проницаемость среды, μ0 — магнитная постоянная. 11.а) Электромагнитные колебания — это периодические изменения со временем электрических и магнитных величин (заряда, силы тока, напряжения, напряженности, магнитной индукции и др.) в электрической цепи. Для возбуждения и поддержания электромагнитных колебаний требуются определенные системы, простейшей из которых является колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (это может быть сопротивление провода катушки и проводов, соединяющих катушку с конденсатором) (рис. 1). Идеальный контур Томсона — колебательный контур без активного сопротивления (R = 0).
Отсчет времени t мы начинаем с момента подключения к контуру заряженного конденсатора. В этот момент (рис. 2, а) напряженность электрического поля
Рис. 2При этом вся энергия W колебательного контура заключена в электрическом поле конденсатора, т.е.
В результате конденсатор перезаряжается: нижняя обкладка конденсатора получает избыточный положительный заряд, а верхняя — отрицательный. Следовательно, в конденсаторе появляется электрическое поле, напряженность которого направлена снизу вверх. В указанном интервале времени сила тока I в контуре и индукция К моменту времени
К моменту времени
К моменту времени Значит, вся энергия колебательного контура заключена теперь в его электрическом поле, т.е.
Таким образом, завершилось полное колебание. В дальнейшем процесс повторяется в уже описанном порядке. Электромагнитные затухающие колебания возникают в э лектромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).
- на активном сопротивлении: ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: Подставим значения UR, UC, Сила тока определяется как производная от заряда
Обозначим
Амплитуда затухающих колебаний заряда имеет вид: Частота затухающих колебаний в LCR – контуре:
Возьмем уравнение для заряда в виде где Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу. Энергия колебаний в контуре складывается из энергии электрического поля
и энергии магнитного поля
Полная энергия в любой момент времени:
где W0 – полная энергия контура в момент времени t=0.
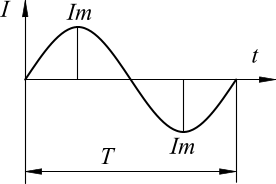
12.а) Электрический ток называется переменным, если он в течение времени меняет свое направление и непрерывно изменяется по величине. Переменный ток, который используется для подключения бытовых или производственных электрических приборов, изменяется по синусоидальному закону: i = I m sin(2πft)
· i – мгновенное значение тока · Im – амплитудное или наибольшее значение тока · f – значение частоты переменного тока · t – время Широко используется переменный ток благодаря тому, что электроэнергия переменного тока технически просто и экономно может быть преобразована из энергии более низкого напряжения в энергию более высокого напряжения и наоборот. Это свойство переменного тока позволяет передавать электроэнергию по проводам на большие расстояния. Промышленный переменный электрический ток получают при помощи электрических генераторов, принцип работы которых основан на законе электромагнитной индукции. Вращение генератора осуществляется механическим двигателем, использующим тепловую, гидравлическую или атомную энергию. Переменный однофазный электрический ток имеет следующие основные характеристики: f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц (Гц): 1гц = 10 3 кгц = 10 6 мгц
1c = 10 3 мс = 10 6 мкс = 10 12 нс В Российской Федерации период Τ переменного тока принят равным 0,02 секунды,следовательно по формуле, f = 1/Τ можно определить частоту переменного тока: f = 1/0,02 = 50 Гц, ω – угловая скорость Помимо частоты f при изучении цепей переменного тока вводится понятие угловой скорости ω. Угловая скорость ω связана с частотой f следующим соотношением: ω=2πf При частоте 50 Гц угловая скорость равна 314 рад/с (2 × 3,14 × 50 = 314). Мгновенное значение (i,u,e,p) – значение величины в данный момент, мгновенное. Максимальное или амплитудное значение (Im,Um,Em,Pm). Эффективное значение тока – это величина переменного тока, равная такому току, который на сопротивлении R, создаёт тепловыделение равное данному переменному току, за тоже время t (I,U,E,P).
Б) 1. Участок цепи, содержащий активное сопротивление Зададимся изменением тока в резисторе по синусоидальному закону i(t) = ImR sin(ωt + ψi). Воспользуемся законом Ома для мгновенных значений тока и напряжения u(t) = R i(t) и получим (2.13) u(t) = R ImR sin(ωt + ψi). Формальная запись синусоидального напряжения имеет вид (2.14) u(t) = UmR sin(ωt + ψu) Соотношения (2.13) и (2.14) будут равны если будут выполнены условия равенства амплитуд и фаз (2.15) UmR = R ImR, (2.16) ψu = ψi. Соотношение (2.15) может быть записано для действующих значений (2.17) UR = R IR. Соотношение (2.16) показывает, что фазы напряжения и тока в резисторе совпадают. Графически это представлено на временной диаграмме (рис. 2.7) и на комплексной плоскости (рис. 2.8).
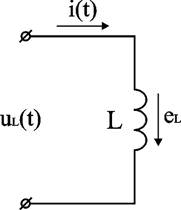
2. Участок цепи, содержащий идеальную индуктивность (рис 2.9)
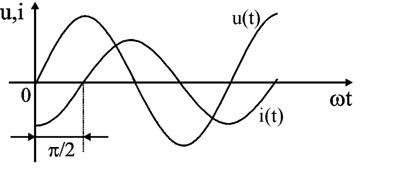
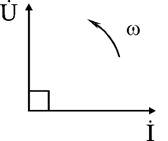
Зададим изменение тока в индуктивности по синусоидальному закону i(t) = ImL sin(ωt + ψi). Используем уравнение связи между током и напряжением в индуктивности uL = L · di / dt и получим uL(t) = ωL · ImL cos(ωt + ψi). Заменим cos на sin и получим (2.18) uL(t) = ωL · ImL sin(ωt + ψi + 90°). Формальная запись синусоидального напряжения имеет вид (2.19) uL(t) = UmL sin(ωt + ψu). Соотношения (2.18) и (2.19) будут равны если выполняется условие равенства амплитуд и фаз (2.20) UmL = ωL · ImL, (2.21) ψu = ψi + 90°. Уравнение (2.20) можно переписать для действующих значений (2.22) UL = ωL · IL. Уравнение (2.21) показывает, что фаза тока в индуктивности отстает от фазы напряжения на 90°. Величину XL = ωL в уравнении (2.20) называют индуктивным сопротивлением. Единицей его измерения является Ом. Графически электрические процессы в индуктивности представлены на рис. 2.10, 2.11.
Рис. 2.10 и 2.11
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.49 (0.011 с.) |

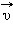 и вектором магнитной индукции
и вектором магнитной индукции 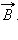 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов 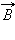 и
и 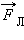 для положительно заряженной частицы показано на рис. 4.18.1.
для положительно заряженной частицы показано на рис. 4.18.1.
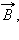 помноженной на заряд q.
помноженной на заряд q.
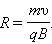
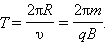
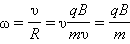
 3
3
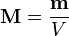 Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как
Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как  и является функцией координат.Связь между M и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля):
и является функцией координат.Связь между M и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля): 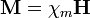
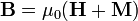
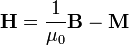 , где
, где 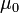 - магнитная постоянная. В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см. Магнитная проницаемость, также см.Магнитная восприимчивость). В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряженность магнитного поля совпадает с вектором магнитной индукции. В магнетиках (магнитных средах) напряженность магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».
- магнитная постоянная. В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см. Магнитная проницаемость, также см.Магнитная восприимчивость). В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряженность магнитного поля совпадает с вектором магнитной индукции. В магнетиках (магнитных средах) напряженность магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».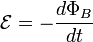 где
где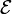 — электродвижущая сила, действующая вдоль произвольно выбранного контура,
— электродвижущая сила, действующая вдоль произвольно выбранного контура, 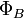
 — магнитный поток через поверхность, натянутую на этот контур.Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца: Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток. Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
— магнитный поток через поверхность, натянутую на этот контур.Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца: Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток. Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом: 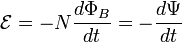 где
где 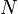 — число витков,
— число витков, 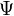 — потокосцепление катушки.
— потокосцепление катушки. , пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величинаэлектродвижущей силы, ответственной за этот ток, определяется уравнением[1]:
, пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величинаэлектродвижущей силы, ответственной за этот ток, определяется уравнением[1]:  где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.
где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.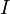 :
: .
.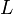 называется коэффициентом самоиндукции или индуктивностью контура (катушки).
называется коэффициентом самоиндукции или индуктивностью контура (катушки).
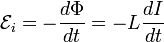 .Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
.Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]: 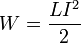 .Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определенную эффективную индуктивность, используемую в расчетах полностью (хотя вообще говоря с определенными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.1)Индуктивность[10] всегда положительна.2)Индуктивность зависит только от геометрических размеров контура и магнитных свойств среды (сердечника).
.Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см. Гиратор); такому элементу можно приписать определенную эффективную индуктивность, используемую в расчетах полностью (хотя вообще говоря с определенными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.1)Индуктивность[10] всегда положительна.2)Индуктивность зависит только от геометрических размеров контура и магнитных свойств среды (сердечника). Среднее значение ЭДС самоиндукции, препятствующей увеличению тока в контуре,
Среднее значение ЭДС самоиндукции, препятствующей увеличению тока в контуре, 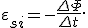 За время Δt через контур переносится заряд
За время Δt через контур переносится заряд 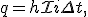 где
где 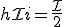 - среднее значение силы тока за время Δt при равномерном его возрастании. Если изменение тока происходит не равномерно, то необходимо рассматривать малые промежутки времени, в течение которых можно считать ЭДС скорость изменения
- среднее значение силы тока за время Δt при равномерном его возрастании. Если изменение тока происходит не равномерно, то необходимо рассматривать малые промежутки времени, в течение которых можно считать ЭДС скорость изменения  постоянной).
постоянной).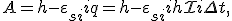

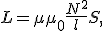 магнитная индукция поля внутри соленоида
магнитная индукция поля внутри соленоида 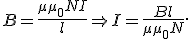 Подставив эти значения L и I в формулу для энергии, получим
Подставив эти значения L и I в формулу для энергии, получим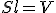 — объем соленоида, то
— объем соленоида, то 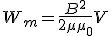 — энергия магнитного поля соленоида с током.
— энергия магнитного поля соленоида с током.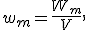 равная энергии магнитного поля, заключенной в единичном объеме этого поля, называется объемной плотностью энергии магнитного поля. Ее можно рассчитать по формуле
равная энергии магнитного поля, заключенной в единичном объеме этого поля, называется объемной плотностью энергии магнитного поля. Ее можно рассчитать по формуле
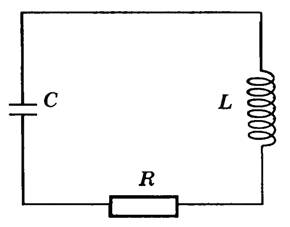 Рис. 1 Рассмотрим свободные электромагнитные колебания — колебания, происходящие в идеальном колебательном контуре за счет расходования сообщенной этому контуру энергии, которая в дальнейшем не пополняется. Рисунок 2 иллюстрирует характерные стадии колебаний в контуре за один период.
Рис. 1 Рассмотрим свободные электромагнитные колебания — колебания, происходящие в идеальном колебательном контуре за счет расходования сообщенной этому контуру энергии, которая в дальнейшем не пополняется. Рисунок 2 иллюстрирует характерные стадии колебаний в контуре за один период.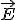 в конденсаторе (направленная сверху вниз), а также напряжение U на обкладках конденсатора максимальны, а тока в контуре еще нет, следовательно, отсутствует и магнитное поле.
в конденсаторе (направленная сверху вниз), а также напряжение U на обкладках конденсатора максимальны, а тока в контуре еще нет, следовательно, отсутствует и магнитное поле.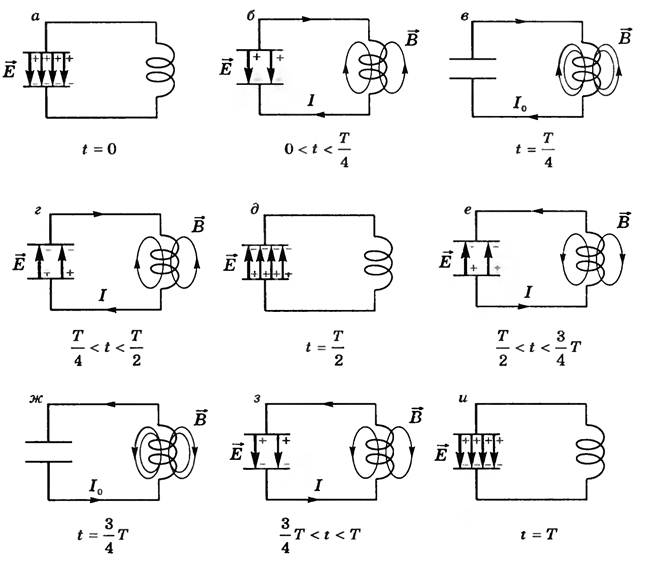
 В промежутке времени от 0 до
В промежутке времени от 0 до 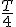 (рис. 2, б) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая нарастанию этого тока. При разряде конденсатора уменьшаются напряженность электрического поля
(рис. 2, б) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая нарастанию этого тока. При разряде конденсатора уменьшаются напряженность электрического поля  магнитного поля, создаваемого этим током, увеличиваются, т.е. возрастает энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки.К моменту времени
магнитного поля, создаваемого этим током, увеличиваются, т.е. возрастает энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки.К моменту времени 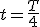 (рис. 2, в) конденсатор полностью разряжается, напряжение U между его обкладками становится равным нулю, и электрическое поле в нем отсутствует
(рис. 2, в) конденсатор полностью разряжается, напряжение U между его обкладками становится равным нулю, и электрическое поле в нем отсутствует 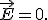 К этому времени ток 1 в контуре и индукция
К этому времени ток 1 в контуре и индукция 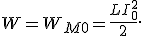 В промежутке времени от
В промежутке времени от  до
до  при уменьшении тока в катушке возникает ЭДС самоиндукции и индукционный ток, направление которого, согласно правилу Ленца, совпадает с направлением убывающего разрядного тока.
при уменьшении тока в катушке возникает ЭДС самоиндукции и индукционный ток, направление которого, согласно правилу Ленца, совпадает с направлением убывающего разрядного тока.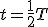 (рис. 2, д) ток в контуре прекращается, следовательно, исчезает магнитное поле
(рис. 2, д) ток в контуре прекращается, следовательно, исчезает магнитное поле 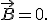 Напряженность электрического поля
Напряженность электрического поля 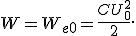 в промежутке времени от
в промежутке времени от 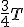 (рис. 2, е) конденсатор вновь разряжается и создает в контуре ток. Однако теперь положительно заряжена нижняя обкладка конденсатора, поэтому направление тока I в контуре меняется на противоположное. Меняется и направление индукции
(рис. 2, е) конденсатор вновь разряжается и создает в контуре ток. Однако теперь положительно заряжена нижняя обкладка конденсатора, поэтому направление тока I в контуре меняется на противоположное. Меняется и направление индукции 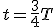 (рис. 2, ж) конденсатор полностью разряжается, напряжение U между его обкладками падает до нуля, электрическое поле исчезает
(рис. 2, ж) конденсатор полностью разряжается, напряжение U между его обкладками падает до нуля, электрическое поле исчезает  а ток I в контуре и индукция
а ток I в контуре и индукция 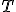 (рис. 14.2, з) сила тока уменьшается, а возникшая в катушке ЭДС самоиндукции препятствует этому. На верхней пластине появляются избыточные положительные заряды, а на нижней — отрицательные. В конденсаторе появляется электрическое поле, напряженность
(рис. 14.2, з) сила тока уменьшается, а возникшая в катушке ЭДС самоиндукции препятствует этому. На верхней пластине появляются избыточные положительные заряды, а на нижней — отрицательные. В конденсаторе появляется электрическое поле, напряженность 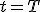 (рис. 2, и) ток в контуре прекращается, исчезает магнитное поле, а напряженность
(рис. 2, и) ток в контуре прекращается, исчезает магнитное поле, а напряженность 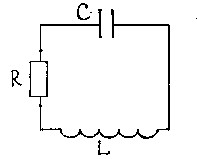 Рисунок 3.3. Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура.Падение напряжения:
Рисунок 3.3. Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура.Падение напряжения: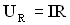 , где I – сила тока в контуре;- на конденсаторе (С):
, где I – сила тока в контуре;- на конденсаторе (С):  , где q – величина заряда на одной из обкладок конденсатора.
, где q – величина заряда на одной из обкладок конденсатора.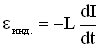 (закон Фарадея).
(закон Фарадея). в уравнение, отражающее закон Кирхгофа, получим:
в уравнение, отражающее закон Кирхгофа, получим:  .
. , тогда
, тогда 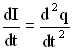 , и дифференциальное уравнение примет вид:
, и дифференциальное уравнение примет вид: .
.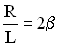 ,
, 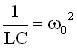 , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
, получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде: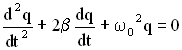 Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид: или
или 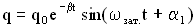 .
.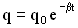 , где
, где  .
. . Период затухающих электромагнитных колебаний:
. Период затухающих электромагнитных колебаний: 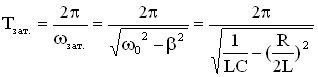 .
. .Величина
.Величина 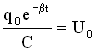 называется амплитудой напряжения на конденсаторе. Токв контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение
называется амплитудой напряжения на конденсаторе. Токв контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение 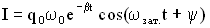 ,
, - начальная фаза.
- начальная фаза.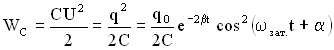
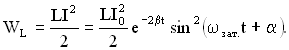
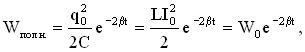
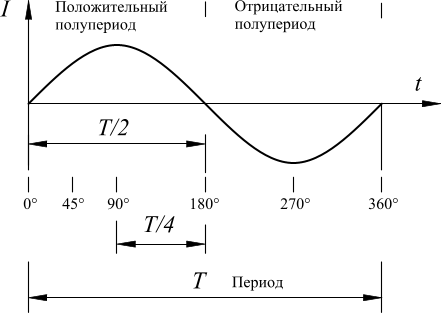 Τ – период – время одного полного изменения переменной величины.Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц (Герц).
Τ – период – время одного полного изменения переменной величины.Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц (Герц).