
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Участок цепи, содержащий ёмкость зададим изменение тока в емкости по синусоидальному законуСодержание книги
Поиск на нашем сайте
i(t) = ImC sin(ωt + ψi). Используем уравнением связи между током и напряжением в емкости uC = 1 / C · ∫ i dt, и получим uC = 1 / (ωC) · ImC (-cos(ωt + ψi)). Заменим –cos на sin (2.23) uC = 1 / (ωC) · ImC sin(ωt + ψi - 90°). Формальная запись синусоидального напряжения имеет вид (2.24) uC = UmC sin(ωt + ψu). Соотношения (2.23) и (2.24) будут равны если выполняется условие равенства амплитуд и фаз (2.25) UmC = 1 / (ωC) · ImC, (2.26) ψu = ψi - 90°. Уравнение (2.25) можно переписать для действующих значений(2.27) UC = 1 / (ωC) · IC. Уравнение (2.26) показывает, что фаза напряжения в емкости отстает от фазы тока на 90°. Величину XC = 1 / (ωC) в уравнении (2.25) называют емкостным сопротивлением цепи и измеряют его в Омах. Графически электрические процессы в емкости представлены на рис. 2.13, 2.14.
В) Протекающий по обмотке переменный ток создает магнитный поток. Этот магнитный поток точно так же, как и ток, изменяет свою силу и направление. При изменении магнитного потока по закону индукции в обмотке создается ЭДС (электродвижущая сила). Направление ЭДС противоположно полярности подаваемого напряжения. Это явление называется самоиндукцией. Самоиндукция в цепи переменного тока частично проявляется в сдвиге по фазе между током и напряжением и частично — в падении индуктивного напряжения. Сопротивление цепи переменного тока становится значительно выше рассчитанного или измеренного сопротивления этой же цепи постоянному току. Сдвиг по фазе между током и напряжением обозначается углом φ. Индуктивное сопротивление (реактивное) обозначается X, активное сопроти ние — R, кажущееся сопротивление цепи или проводника — Z. Полное сопротивление (импеданс) вычисляется по формуле:
Закон Ома для цепи переменного тока: U=I*Z Где: поэтому мощность P полная (произведение тока и напряжения) = 220*значение тока полное.
13.а) ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ - это электромагнитное поле, распространяющееся в пространстве с конечной скоростью,
Свойства электромагнитных волн:
Источником электромагнитных волн являются ускоренно движущиеся электрические заряды. г) ШКАЛА ЭЛЕКТРОМАГНИТНЫХ ВОЛН Все окружающее нас пространство пронизано электромагнитным излучением. Солнце, окружающие нас тела, антенны передатчиков испускают электромагнитные волны, которые в зависимости от их частоты колебаний носят разные названия. Метры
Радиоволны—это электромагнитные волны (c длиной волны от более чем 10000м до 0,005м), служащие для передачи сигналов (информации) на расстояние без проводов. Электромагнитные излучения с длиной волны, меньшей чем 0,005м, но большей чем 770 нм, т. е. лежащие между диапазоном радиоволн и диапазоном видимого света, называются инфракрасным излучением (ИК). К видимому свету относят излучения с длинной волны примерно от 770нм до 380нм, от красного до фиолетового света. Значения этого участка спектра электромагнитных излучений в жизни человека исключительно велико, так как почти все сведения об окружающем мире человек получает с помощью зрения. Свет является обязательным условием для развития зеленых растений и, следовательно, необходимым условием для существования жизни на Земле. Невидимое глазом электромагнитное излучение с длиннной волны меньше, чем у фиолетового света, называют ультрафиолетовым излучением (УФ).. Ультрафиолетовые излучение способно убивать белезнетворных бактерий, поэтому его широко применяют а медицине. Ультрафиолетовое излучение в составе солнечного света вызывает биологические процессы, приводящие к потемнению кожи человека – загару. В качестве источников ультрафиолетового излучения в медицине используются газоразрядные лампы. Трубки таких ламп изготовляют из кварца, прозрачного для ультрафиолетовых лучей; поэтому эти лампы называют кварцевыми лампами.
Рентгеновские лучи (Ри) невидимы глазом. Они проходят без существенного поглощения через значительные слои вещества, непрозрачного для видимого света. Обнаруживают рентгеновские лучи по их способности вызывать определенное свечение некоторых кристаллов и действовать на фотопленку. Способность рентгеновских лучей проникать через толстые слои вещества используется для диагностики заболеваний внутренних органов человека. В технике рентгеновские лучи применяются для контроля внутренней структуры различных изделий, сварных швов. Рентгеновское излучение обладает сильным биологическим действием и применяется для лечения некоторых заболеваний. Гамма-излучением называют электромагнитное излучение, испускаемое возбужденными ядрами и возникающее при взаимодействии элементарных частиц.
В) 1. Из теории Максвелла вытекает, что если в какой-либо малой области пространства периодически изменять электрическое и магнитное поля, то эти изменения должны периодически повторяться и во всех других точках пространства, причем в каждой последующей несколько позже, чем в предыдущей, т.е. от источника электромагнитных колебаний должны во все стороны распространяться электромагнитные волны с определенной скоростью. Вывод о конечности скорости распространения электромагнитных волн — очень важное следствие из теории Максвелла. Дж. Максвелл чисто математически показал, что скорость распространения электромагнитного поля в вакууме равна скорости света
2. При распространении электромагнитных волн в каждой точке пространства происходят периодически повторяющиеся изменения электрического и магнитного полей. Эти изменения удобно изображать в виде колебаний векторов напряженности электрического поля
Рис. 2. 5. Период электромагнитной волны (частота) равен периоду (частоте) колебаний источника электромагнитных волн. Для электромагнитных волн справедливо соотношение
В вакууме 6. Электромагнитная волна, как и упругая, является носителем энергии, причем перенос энергии совершается в направлении распространения волны. Энергию где V — объем среды, в котором сосредоточена электромагнитная волна. Переносимая энергия пропорциональна четвертой степени частоты. Поэтому источником интенсивных электромагнитных волн, способных переносить электромагнитную энергию на значительные расстояния, должны быть электромагнитные колебания очень высокой частоты (порядка миллиона герц). Понятно, что никакие механические генераторы не могут создать переменный ток частотой -106Гц (для этого якорь должен был бы совершать 106 оборотов в 1 с). Источником электромагнитных волн такой частоты может быть только колебательный контур. 7. Электромагнитные волны распространяются прямолинейно в однородной среде, испытывают преломление при переходе из одной среды в другую, отражаются от преград. Для них характерны явления дифракции и интерференции. 14.а) Геометрическая оптика — раздел оптики, в котором изучаются законы распространения света на основе положений о световых лучах. Б) Световой луч принят как линия, вдоль которой распространяется поток световой (квантовой) энергии.Понятие луча согласуется с реальностью только в том случае, когда можно пренебрегать дифракцией света на оптических неоднородностях. Это допустимо в случае, когда длина световой волны намного меньше размеров неоднородностей. Законы геометрической оптики позволяют создать упрощённую и в большинстве случаев достаточно точную теорию оптических систем. На основе геометрической оптики можно объяснять образование оптических изображений, возможность вычислять аберрации оптических систем и разрабатывать методы их исправления; вывести энергетические соотношения в световых пучках, проходящих через оптические системы. Однако волновые явления, в том числе дифракционные, влияющие на качество изображений и определяющие разрешающую способность оптических приборов, в геометрической оптике не рассматриваются
В) Основные законы геометрической оптики были известны задолго до установления физической природы света. Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны. Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики при λ → 0. Границы применимости геометрической оптики будут рассмотрены в разделе о дифракции света. На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а часть пройдет через границу и продолжит распространяться во второй среде. Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α. Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:
Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом в 1621 г. Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:
Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ1 к скорости их распространения во второй среде υ2:
Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:
Рис 3.1.1 иллюстрирует законы отражения и преломления света.
Среду с меньшим абсолютным показателем преломления называют оптически менее плотной. При переходе света из оптически более плотной среды в оптически менее плотную n 2 < n 1 (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол αпр, который называется предельным углом полного внутреннего отражения (см. рис. 3.1.2). Для угла падения α = αпр sin β = 1; значение sin αпр = n 2 / n 1 < 1. Если второй средой является воздух (n 2 ≈ 1), то формулу удобно переписать в виде
где n = n 1 > 1 – абсолютный показатель преломления первой среды. Для границы раздела стекло–воздух (n = 1,5) критический угол равен αпр = 42°, для границы вода–воздух (n = 1,33) αпр = 48,7°.
Явление полного внутреннего отражения находит применение во многих оптических устройствах. Наиболее интересным и практически важным применением является создание волоконных световодов, которые представляют собой тонкие (от нескольких микрометров до миллиметров) произвольно изогнутые нити из оптически прозрачного материала (стекло, кварц). Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей (рис 3.1.3). Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой.
Г)
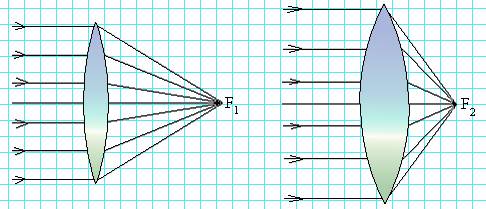
Изображением точки S в линзе будет точка пересечения всех преломленных лучей или их продолжений. В первом случае изображение действительное, во втором — мнимое. Как всегда, чтобы найти точку пересечения всех лучей, достаточно построить любые два. Мы можем это сделать, пользуясь вторым законом преломления. Для этого надо измерить угол падения произвольного луча, сосчитать угол преломления, построить преломленный луч, который под каким-то углом упадет на другую грань линзы. Измерив этот угол падения, надо вычислить новый угол преломления и построить выходящий луч. Как видите, работа достаточно трудоемкая, поэтому обычно ее избегают. По известным свойствам линз можно построить три луча без всяких вычислений. Луч, падающий параллельно какой-либо оптической оси, после двойного преломления пройдет через действительный фокус или его продолжения пройдет через мнимый фокус. По закону обратимости луч, падающий по направлению на соответствующий фокус, после двойного преломления выйдет параллельно определенной оптической оси. Наконец, через оптический центр линзы луч пройдет, не отклоняясь. На рис. 7 построено изображения точки S в собирающей линзе, на рис. 8 — в рассеивающей. При таких построениях изображают главную оптическую ось и на ней показывают фокусные расстояния F (расстояния от главных фокусов или от фокальных плоскостей до оптического центра линзы) и двойные фокусные расстояния (для собирающих линз). Затем ищут точку пересечения преломленных лучей (или их продолжений), используя любые два из вышеперечисленных. Обычно вызывает затруднение построение изображения точки, расположенной на главной оптической оси. Для такого построения нужно взять любой луч, который будет параллелен какой-то побочной оптической оси (пунктир на рис. 9). После двойного преломления он пройдет через побочный фокус, который лежит в точке пересечения этой побочной оси и фокальной плоскости. В качестве второго луча удобно использовать луч, идущий без преломления вдоль главной оптической оси.
На рис. 10 изображены две собирающие линзы. Вторая «лучше» собирает лучи, ближе их сводит, она «сильнее». Оптической силой линзы называется величина, обратная фокусному расстоянию:
Выражается оптическая сила линзы в диоптриях (дптр).
Одна диоптрия — оптическая сила такой линзы, фокусное расстояние которой 1 м. У собирающих линз положительная оптическая сила, у рассеивающих — отрицательная. Построение изображения предмета в собирающей линзе сводится к построению его крайних точек. В качестве предмета выберем стрелку АВ (рис. 11). Изображение точки A построено, как на рис. 7, точка B1 может быть найдена, как на рис 19. Введем обозначение (аналогичные введенным при рассмотрении зеркал): расстояние от предмета до линзы | BO | = d; расстояние от предмета до линзы изображения| BO 1| = f, фокусное расстояние | OF | = F. Из подобия треугольников A 1 B 1 O и АВО (по равным острым — вертикальным — углам прямоугольные треугольники подобны)
Разделив уравнение почленно на dFf и перенеся отрицательный член в другую сторону равенства, получим:
Мы вывели формулу линзы, аналогичную формуле зеркала. В случае рассеивающей линзы (рис. 22) «работает» ближний мнимый фокус. Обратите внимание на то, что точка А1 является точкой пересечения продолжения преломленных лучей, а не точкой пересечения преломленного луча FD и падающего луча AO.
Для доказательства рассмотрите луч, падающий из точки А по направлению на дальний фокус. После двойного преломления он выйдет из линзы параллельно главной оптической оси, так что его продолжение пройдет через точку А1. Изображение точки В может быть построено аналогично рис. 9. Из подобия соответствующих треугольников
Эту формулу рассеивающей линзы можно получить из (*). Для этого условимся считать положительными величины d (от предмета до линзы), f (от линзы до изображения) и F (от линзы до фокуса), если они направлены в сторону падающих лучей. Тогда в формуле (*) для собирающей линзы все члены положительны, для рассеивающей — расстояние от предмета до линзы положительно, d > 0, а расстояния от линзы до изображения и до фокуса отрицательны (f < 0, F < 0). Если перейти к абсолютным значениям расстояний, то получим
Линейным увеличением линзы называется число, показывающее, во сколько раз линейные размеры изображения больше линейных размеров предмета. Из подобия рассмотренных треугольников имеем
Можно провести исследования формулы линзы, аналогичное исследованию формулы зеркала. Как изменится изображение предмета, если его половина линзы разбилась? Изображение станет менее интенсивным, но ни его форма, ни расположение не изменятся. Аналогично изображение предмета в любом кусочке линзы или зеркала. Для построения изображения точки в идеальной системе достаточно построить любые два луча, идущие от этой точки. Точка пересечения выходящих лучей, соответствующих этим двум падающим, будет искомым изображением данной точки.
15.а) Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при определенных условиях при наложении двух или нескольких световых пучков. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света. Первый эксперимент по наблюдение интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 6.7.1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 6.7.2).
Ньютон не смог объяснить с точки зрения корпускулярной теории, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов (см. § 6.6). Исторически первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 6.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые можно рассматривать в соответствии с принципом Гюйгенса как источники вторичных волн, освещались светом одного источника S.При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1 и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2 распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.Монохроматическая волна, распространяющаяся в направлении радиус-вектора
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
Не существует приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2. Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
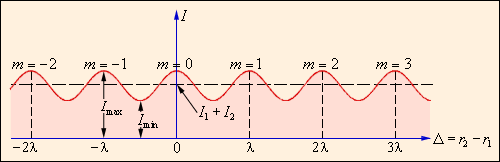
где Δ = r2 – r1 – так называемая разность хода. Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2,...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 < I1 + I2. На рис. 6.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.
В частности, если I1 = I2 = I0, то есть интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
В этом случае Imax = 4I0, Imin = 0. Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты. Различие проявляются только в том, как зависит разность хода Δ от положения точки наблюдения P. Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, то есть при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
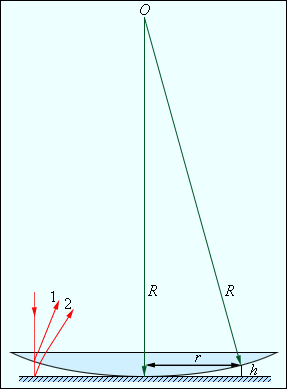
где ψ – угол схождения «лучей» в точке наблюдения P. Выполним количественную оценку. Допустим, что расстояние d между щелями S1 и S2 равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 105 нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика. Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек. В эксперименте Ньютона (рис. 6.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Для случая, когда радиус кривизны R линзы велик по сравнению с h, можно приближенно получить:
где r – смещение от оси симметрии. При написании выражения для разности хода следует также учесть, что волны 1 и 2 отражаются при разных условиях. Первая волна отражается от границы стекло–воздух, а вторая – от границы воздух–стекло. Во втором случае происходит изменение фазы колебаний отраженной волны на π, что эквивалентно увеличению разности хода на λ / 2. Поэтому
При r = 0, то есть в центре (точка соприкосновения) Δ = λ / 2; поэтому в центре колец Ньютона всегда наблюдается интерференционный минимум – темное пятно. Радиусы rm последующих темных колец определяются выражением
Эта формула позволяет экспериментально определить длину волны света λ, если известен радиус кривизны R линзы. Проблема когерентности волн. Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волн одной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), и в каких случаях нужно складывать интенсивности волн, то есть квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос. Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10–8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τ вся совокупность излучающих атомов обновляется.Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ. Отдельные «обрывки» излучения длительности τ называются цугами. Цуги имеют пространственную длину, равную cτ, где c – скорость света. Колебания в разных цугах не согласованы между собой. Таким образом, реальная световая волна представляет собой последовательность волновых цугов с беспорядочно меняющейся фазой. Принято говорить, что колебания в разных цугах некогерентны. Интервал времени τ, в течении которого фаза колебаний остается приблизительно постоянной, называют временем когерентности. Интерференция может возникнуть только при сложении когерентных колебаний, то есть колебаний, относящихся к одному и тому же цугу. Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз оказывается случайной функцией времени. Интерференционные полосы испытывают беспорядочные перемещения из стороны в сторону, и за время Δt их регистрации, которая в оптических экспериментах значительно больше времени когерентности (Δt >> τ), происходит полное усреднение. Регистрирующее устройс
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.203.186 (0.019 с.) |



 Где:
Где: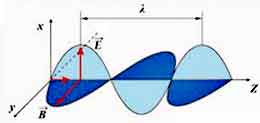
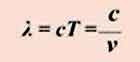


 Рисунок 3.5.6.4.
Структура электромагнитной волны.
Это можно обнаружить, повернув передающий или приемный рупор на 90°. Звук при этом исчезает.
Поляризацию наблюдают, помещая между генератором и приемником решетку из параллельных металлических стержней (рис. 3.5.6.5). Решетку располагают так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка отражает волны, подобно сплошной металлической пластине.
Рисунок 3.5.6.4.
Структура электромагнитной волны.
Это можно обнаружить, повернув передающий или приемный рупор на 90°. Звук при этом исчезает.
Поляризацию наблюдают, помещая между генератором и приемником решетку из параллельных металлических стержней (рис. 3.5.6.5). Решетку располагают так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка отражает волны, подобно сплошной металлической пластине.
 а в среде эта скорость ν меньше и зависит от свойств среды:
а в среде эта скорость ν меньше и зависит от свойств среды: где ε — диэлектрическая проницаемость среды, μ — магнитная проницаемость среды.
где ε — диэлектрическая проницаемость среды, μ — магнитная проницаемость среды.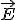 и индукции магнитного поля
и индукции магнитного поля  в каждой точке пространства. Электромагнитная волна — поперечная волна, так как
в каждой точке пространства. Электромагнитная волна — поперечная волна, так как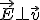 и
и  3. Колебания векторов
3. Колебания векторов  в каждой точке пространства. 4. Векторы
в каждой точке пространства. 4. Векторы  правовинтовую систему (рис. 2): если головку правого винта расположить в плоскости векторов
правовинтовую систему (рис. 2): если головку правого винта расположить в плоскости векторов 

 длина волны наибольшая по сравнению с λ в другой среде, так как ν = const и изменяются только
длина волны наибольшая по сравнению с λ в другой среде, так как ν = const и изменяются только  и
и  к при переходе от одной среды к другой.
к при переходе от одной среды к другой. электромагнитной волны можно рассчитать по формуле
электромагнитной волны можно рассчитать по формуле

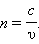



 Рис. 7
Рис. 7
 Рис. 8
Рис. 8
 Рис. 9
Рис. 9

 . Из подобия треугольников A 1 B 1 F и DOF (по тому же признаку подобия)
. Из подобия треугольников A 1 B 1 F и DOF (по тому же признаку подобия)  . Следовательно,
. Следовательно, или fF = df − dF.
или fF = df − dF.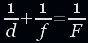 (*)
(*) Рис. 11
Рис. 11
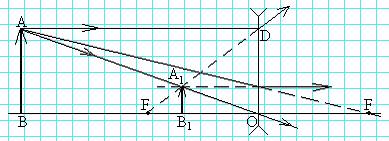 Рис. 12
Рис. 12
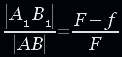 ; fF = dF − df или
; fF = dF − df или
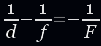 или
или 
 1
1
 , записывается в виде
, записывается в виде
 4
4








