
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По сути этот парадокс показал если не внутреннюю противоречивость классической физики, то во всяком случае крайне резкое (абсурдное) расхождение с элементарными наблюдениями и экспериментом.Содержание книги
Поиск на нашем сайте
Так как это не согласуется с экспериментальным наблюдением, в конце 19 века возникали трудности в описании фотометрических характеристик тел. Проблема была решена при помощи квантовой теории излучения Макса Планка в 1900 году.
19.а) Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект. Законы фотоэффекта: Формулировка 1-го закона фотоэффекта: количество электронов, вырываемых светом с поверхности металла за единицу времени на данной частоте, прямо пропорционально световому потоку, освещающему металл. Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности. 3-ий закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света (или максимальная длина волны λ0), при которой ещё возможен фотоэффект, и если, то фотоэффект уже не происходит. Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода, покидает металл:, где — максимальная кинетическая энергия, которую может иметь электрон при вылете из металла. Б) Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком. Фотокатод — электрод вакуумного электронного прибора, непосредственно подвергающийся воздействию электромагнитных излучений и эмитирующий электроны под действием этого излучения. Зависимость спектральной чувствительности от частоты или длины волны электромагнитного излучения называют спектральной характеристикой фотокатода. Законы внешнего фотоэффекта 1. Закон Столетова: при неизменном спектральном составе электромагнитных излучений, падающих на фотокатод, фототок насыщения пропорционален энергетической освещенности катода (иначе: число фотоэлектронов, выбиваемых из катода за 1 с, прямо пропорционально интенсивности излучения): 2. Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой. 3. Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота ν0 света (зависящая от химической природы вещества и состояния поверхности), ниже которой фотоэффект невозможен. В) А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе предложенной им квантовой теории фотоэффекта. Согласно Эйнштейну, свет частотой n не только испускается, как это предполагал Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых e 0= hn. Таким образом, распространение света нужно рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных световых квантов, движущихся со скоростью с распространения света в вакууме. Кванты электромагнитного излучения получили название фотонов. По Эйнштейну, каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности света (I закон фотоэффекта). Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно. Энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии mv 2max/2. По закону сохранения энергии,
Уравнение (203.1) называется уравнением Эйнштейна для внешнего фотоэффекта. Уравнение Эйнштейна позволяет объяснить II и III законы фотоэффекта. Из (203.1) непосредственно следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни n от интенсивности света не зависят (II закон фотоэффекта). Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается (для данного металла А= const), то при некоторой достаточно малой частоте n = n 0 кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится (III закон фотоэффекта). Согласно изложенному, из (203.1) получим, что
и есть красная граница фотоэффекта для данного металла. Она зависит лишь от работы выхода электрона, т. е. от химической природы вещества и состояния его поверхности. Выражение (203.1) можно записать, используя (202.1) и (203.2), в виде
20.а) Атомы представляют собой очень прочные системы, несоизмеримо более устойчивые, чем составленные из атомов молекулы. Такие внешние воздействия, как нагрев, изменение давления, мощные электрические разряды и т.д., приводят лишь к незначительным изменениям атомов: они могут ионизоваться. Поэтому до конца XIX в. атомы считали простейшими неделимыми частицами вещества. Однако последующее развитие науки опровергло эту точку зрения. Было установлено, что атомы представляют собой сложные образования. Об этом свидетельствуют следующие факты. 1.Электромагнитная теория света свидетельствует, что атомы содержат в себе электрические заряды, способные перемещаться. Действительно, согласно теории Максвелла, электромагнитные волны излучают ускоренно движущиеся заряды. Но атомы, как показывал опыт, способны испускать свет, причем не только оптического диапазона — электромагнитные волны. Следовательно, в состав атомов входят ускоренно движущиеся заряды.2.Изучение электропроводности металлов показало, что в состав атомов входят отрицательно заряженные частицы (электроны).3.Закон электролиза, открытый М. Фарадеем, свидетельствовал в пользу существования мельчайших неделимых носителей электрического заряда. При электролизе 1 моль любого n-валентного вещества переносит заряд Кл, где F — постоянная Фарадея. На один ион приходится заряд Кл, где NA — постоянная Авогадро.Эту закономерность легко понять, если принять, что заряд |e|= 1,6 • 10-19 Кл является мельчайшей порцией заряда — элементарным зарядом. Значит, в состав атомов электролитов входят частицы с зарядом e.4.В 1879 г. при пропускании электрического тока через разряженный газ в трубке были обнаружены так называемые катодные лучи, представляющие собой частицы, летящие от катода к аноду. Они отклоняются в электрическом и магнитном полях, дают тень фигурного анода на светящемся стекле и т.д. В 1897 г. Дж. Томсон доказал, что катодные лучи представляют собой поток электронов. Причина их появления — бомбардировка катода ионами разреженного газа, ускоренными в электрическом поле между катодом и анодом. Следовательно, в состав атомов катода входят электроны.5.В. Рентген открыл так называемые Х-лучи (рентгеновские лучи), которые возникали при торможении быстрых электронов у анода. Существование рентгеновских лучей свидетельствовало о каких-то процессах, происходящих внутри атома, о сложном строении самого атома.6.Решающее доказательство того, что в состав любого атома входят и положительно, и отрицательно заряженные частицы, получил французский ученый А. Беккерель. В 1896 г. он обнаружил явление естественной радиоактивности, при котором из атомов вылетают электроны и положительно заряженные частицы, получившие название -частиц.Таким образом, все приведенные факты, а также многие другие явления свидетельствуют о сложной структуре атома. В результате возникла необходимость создания модели атома.Первую модель атома предложил Дж. Томсон. Согласно этой модели, атом представляет собой положительно заряженный шар, внутри которого находится такое количество электронов, чтобы атом в целом был электрически нейтрален. Эти электроны могут совершать колебания, что позволяет объяснить излучение атомом электромагнитных волн.Эта модель имела ряд недостатков.Она не могла объяснить наличие большого числа линий в спектрах атомов.Модель не позволяла объяснить спектральные закономерности в спектре атома водорода (см. § 20.9), найденные эмпирически.Модель Томсона не давала возможности понять, чем определяются размеры атомов.Главный же фактор, заставивший отказаться от модели Томсона, состоял в том. что эта модель оказалась в полном противоречии с опытом Э. Резерфорда. Б) Модель атома Резерфорда (Ядерная или Планетарная модель атома)Рассеяние отдельных α-частиц на большие углы Резерфорд объяснил тем, что положительный заряд в атоме не распределен равномерно в шаре радиусом 10-10 м, как предполагали ранее, а сосредоточен в центральной части атома (атомном ядре) в области значительно меньших размеров. Расчеты Резерфорда показали, что для объяснения опытов по рассеянию α-частиц нужно принять радиус атомного ядра равным примерно 10-15 м.
Планетарная модель атома объясняет основные закономерности рассеяния заряженных частиц. Так как большая часть пространства в атоме между атомным ядром и обращающимися вокруг него электронами пуста, быстро заряженные частицы могут почти свободно проникать через довольно значительные слои вещества, содержащие несколько тысяч слоев атомов.При столкновениях с отдельными электронами быстрые заряженные частицы испытывают рассеяние на очень большие углы, так как масса электрона мала. Однако в тех редких случаях, когда быстрая заряженная частица пролетает на очень близком расстоянии от одного из атомных ядер, под действием силы электрического поля атомного ядра может произойти рассеяние заряженной частицы на любой угол до 180°. В)Квантовые постулаты Бора Датский физик Нильс Бор (1885-1962) обосновал планетарную модель атома Резерфорда. Свои представления об особых свойствах атомов (устойчивости атома и спектральных закономерностей его излучения) Бор сформулировал в виде постулатов следующего содержания: 1. Электрон в атоме можеь находиться только в определенных устойчивых состояниях, называемых стационарными или квантовыми, каждому из которых соответствует определенная энергия En. В этих состояниях атом не излучает электромагнитных волн. Момент импульса электрона, движущегося по стационарной орбите, имеет квантовые значения, удовлетворяющие условию: meυr = nħ (n = 1,2,3,…), где n – главное квантовое число, me – масса покоя электрона, υ – скорость электрона, r – радиус орбиты, ħ – постоянная Планка. 2. При переходе атома из одного стационарного состояния в другое испускается или поглощается квант энергии Δ E = hν. Все стационарные состояния, кроме одного, являются стационарными лишь условно. Бесконечно долго каждый атом может находиться лишь в стационарном состоянии с минимальным запасом энергии. Это состояние атома называется основным. Все остальные стационарные состояния атома называются возбужденными. 21.а) Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантованных полей в квантовой теории поля.Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных волн. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвелла[1]. Тем не менее, эксперимент показывает, что фотон не есть короткий импульс электромагнитного излучения, например, он не может быть разделён на несколько пучков оптическими делителями лучей, что наглядно показал эксперимент, проведённый французскими физиками Гранжье, Роже и Аспэ в 1986 году[2]. Корпускулярные свойства света проявляются при фотоэффекте и в эффекте Комптона. Фотон ведет себя и как частица, которая излучается или поглощается целиком объектами, размеры которых много меньше его длины волны (например, атомными ядрами), или вообще могут считаться точечными (например, электрон).В настоящий момент концепция корпускулярно-волнового дуализма представляет лишь исторический интерес, так как служила только интерпретацией, способом описать поведение квантовых объектов, подбирая ему аналогии из классической физики. На деле квантовые объекты не являются ни классическими волнами, ни классическими частицами, приобретая свойства первых или вторых лишь в некотором приближении. Методологически более корректной является формулировка квантовой теории через интегралы по траекториям (пропагаторная), свободная от использования классических понятий. Такие явления, как интерференция и дифракция света, убедительно свидетельствуют о волновой природе света. В то же время закономерности равновесного теплового излучения, фотоэффекта и эффекта Комптона можно успешно истолковать с классической точки зрения только на основе представлений о свете, как о потоке дискретных фотонов. Однако волновой и корпускулярный способы описания света не противоречат, а взаимно дополняют друг друга, так как свет одновременно обладает и волновыми и корпускулярными свойствами.Волновые свойства света играют определяющую роль в закономерностях его интерференции, дифракции, поляризации, а корпускулярные — в процессах взаимодействия света с веществом. Чем больше длина волны света, тем меньше импульс и энергия фотона и тем труднее обнаружить корпускулярные свойства света. Например, внешний фотоэффект происходит только при энергиях фотонов, больших или равных работе выхода электрона из вещества. Чем меньше длина волны электромагнитного излучения, тем больше энергия и импульс фотонов и тем труднее обнаружить волновые свойства этого излучения. Например, рентгеновское излучение дифрагирует только на очень «тонкой» дифракционной решетке — кристаллической решетке твердого тела. Б)Волны де Бройля Физика атомов, молекул и их коллективов, в частности кристаллов, а также атомных ядер и элементарных частиц изучается в квантовой механике. Квантовые эффекты являются существенными, если характерное значение действия (произведение характерной энергии на характерное время или характерного импульса на характерное расстояние) становится сравнимым с В основе квантовой механики лежат представления Планка о дискретном характере изменения энергии атомов, Эйнштейна офотонах, данные о квантованности некоторых физических величин (например, импульса и энергии), характеризующих в определенных условиях состояния частиц микромира.Де Бройль выдвинул идею о том, что волновой характер распространения, установленный для фотонов, имеет универсальный характер. Он должен проявляться для любых частиц, обладающих импульсом Формула де Бройля устанавливает зависимость длины волны
Другой вид формулы де Бройля:
Длина волны де Бройля для нерелятивистской частицы с массой
Формула де Бройля экспериментально подтверждается опытами по рассеянию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещества. Признаком волнового процесса во всех таких опытах является дифракционная картина распределения электронов (или других частиц) в приемниках частиц. Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным. Впрочем, наблюдать квантовые эффекты можно и в макроскопическом масштабе, особенно ярким примером этому служат сверхпроводимость и сверхтекучесть. Фазовая скорость волн де Бройля свободной частицы
где Групповая скорость волны де Бройля
Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модуля амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определенные места в приёмниках — туда, где интенсивность волны де Бройляоказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль. В) Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых (см. физическая величина), описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей[* 1] задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики. Соотношения неопределённостей Гейзенберга являются теоретическим пределом точности одновременных измерений двух некоммутирующих наблюдаемых. Они справедливы как для идеальных измерений, иногда называемых измерениями фон Неймана, так и для неидеальных измерений. Согласно принципу неопределённостей у частицы не могут быть одновременно точно измерено положение и скорость (импульс)[* 2]. Принцип неопределённости уже в виде, первоначально предложенном Гейзенбергом, применим и в случае, когда ни одна из двух крайних ситуаций (полностью определенный импульс и полностью неопределенная пространственная координата - или полностью неопределенный импульс и полностью определенная координата) не реализуется.Соотношения неопределённостей не ограничивают точность однократного измерения любой величины (для многомерных величин тут подразумевается в общем случае только одна компонента). Если её оператор коммутирует сам с собой в разные моменты времени, то не ограничена точность и многократного (или непрерывного) измерения одной величины. Например, соотношение неопределённостей для свободной частицы не препятствует точному измерению её импульса, но не позволяет точно измерить её координату (это ограничение называется стандартный квантовый предел для координаты).Соотношение неопределенностей в квантовой механике в математическом смысле есть непосредственное прямое следствие некоего свойства преобразования Фурье[* 4].Существует точная количественная аналогия между соотношениями неопределённости Гейзенберга и свойствами волн или сигналов. Рассмотрим переменный во времени сигнал, например звуковую волну. Бессмысленно говорить о частотном спектре сигнала в какой-либо момент времени. Для точного определения частоты необходимо наблюдать за сигналом в течение некоторого времени, таким образом теряя точность определения времени. Другими словами, звук не может одновременно иметь и точное значение времени его фиксации, как его имеет очень короткий импульс, и точного значения частоты, как это имеет место для непрерывного (и в принципе бесконечно длительного) чистого тона (чистой синусоиды). Временно́е положение и частота волны математически полностью аналогичны координате и (квантово-механическому) импульсу частицы. Что совсем не удивительно, если вспомнить, что, то есть импульс в квантовой механике — это и есть пространственная частота вдоль соответствующей координаты. Если имеется несколько (много) идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определённому распределению вероятности — это фундаментальный постулат квантовой механики. Измеряя величину среднеквадратического отклонения
Г) Волнова́я фу́нкция (функция состояния, пси-функция, амплитуда вероятности) — комплексная функция, используемая в квантовой механике для вероятностного описания состоянияквантовомеханической системы. В широком смысле — то же самое, что и вектор состояния.Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы (или физической системы) в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния. Физический смысл квадрата модуля волновой функции Волновая функция
22.а) Квантовые числа и их физический смысл. Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел. "Задайте значения квантовых чисел, и я полностью опишу свойства атома" - так может современный физик перефразировать известное изречение Архимеда.Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома. 1. Главное квантовое число
Можно отметить, что эти значения энергии являются собственными значениями гамильтониана (5.17a). Поэтому в связанном состоянии электрон в атоме водорода имеет дискретный энергетический спектр, лежащий в области отрицательных значений и имеющий точку сгущения 2. Орбитальное (азимутальное) квантовое число
Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:
Проанализируем эту формулу квантования момента импульса. Сравнивая ее с условием (5.3) квантования момента импульса движущегося электрона в теории Бора, можно заметить, что эти условия не совпадают. И дело не только в отличии числовых значений, рассчитанных по этим формулам. Принципиальное отличие этих соотношений состоит в том, что в квантовой механике возможны состояния атома с нулевым моментом импульса. Во всех При классическом описании движения электрона в атоме по определенной траектории (орбите) в любом состоянии атом должен обладать ненулевым моментом импульса. Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами. Следовательно, опыт подтверждает, что только отказ от классического траекторного способа описания движения электрона в атоме позволяет правильно рассчитать и предсказать свойства атома. Вероятностный способ описания движения частиц в квантовой механике является единственно правильным способом описания свойств атомных систем - таков вывод современной физики. Так как движущийся вокруг ядра электрон является заряженной частицей, то такое движение обуславливает протекание некоторого замкнутого тока в атоме, который можно охарактеризовать орбитальным магнитным моментом В теории Бора, когда с позиции классической теории рассматривается круговое движение электрона по орбите радиуса
который можно охарактеризовать величиной магнитного момента
Связь механического и магнитного моментов при этом определяетсягиромагнитным отношением
Так как заряд электрона отрицателен, то для орбитального движения направление вектора магнитного момента
Итак, в любом квантовом состоянии атом водорода обладает не только механическим моментом
Здесь универсальная постоянная
служит единицей измерения магнитных моментов атомов и называетсямагнетоном Бора. Если атом переходит из одного квантового состояния в другое с испусканием (поглощением) фотона излучения, то возможны лишь такие переходы, для которых орбитальное квантовое число | ||||||||||||
|
| Поделиться: |

 и
и 
 (203.1)
(203.1)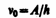 (203.2)
(203.2)
 Резерфорд предположил, что атом устроен подобно планетарной системе. Как вокруг Солнца на больших расстояниях от него
Резерфорд предположил, что атом устроен подобно планетарной системе. Как вокруг Солнца на больших расстояниях от него  обращаются планеты, так электроны в атоме обращаются вокруг атомного ядра. Радиус круговой орбиты самого далекого от ядра электрона и есть радиус атома. Такая модель атома была названа планетарной моделью.
обращаются планеты, так электроны в атоме обращаются вокруг атомного ядра. Радиус круговой орбиты самого далекого от ядра электрона и есть радиус атома. Такая модель атома была названа планетарной моделью. (постоянная Планка). Если частицы движутся со скоростями много меньше, чем скорость света в вакууме
(постоянная Планка). Если частицы движутся со скоростями много меньше, чем скорость света в вакууме  , то применяется нерелятивистская квантовая механика; при скоростях близких к
, то применяется нерелятивистская квантовая механика; при скоростях близких к  . Все частицы, имеющие конечный импульс
. Все частицы, имеющие конечный импульс 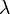 , связанной с движущейся частицей вещества, от импульса
, связанной с движущейся частицей вещества, от импульса  где
где  — масса частицы,
— масса частицы,  — ее скорость,
— ее скорость,  — постоянная Планка. Волны, о которых идет речь, называются волнами де Бройля.
— постоянная Планка. Волны, о которых идет речь, называются волнами де Бройля. где
где  — волновой вектор, модуль которого
— волновой вектор, модуль которого 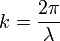 — волновое число — есть число длин волн, укладывающихся на
— волновое число — есть число длин волн, укладывающихся на  единицах длины,
единицах длины,  — единичный вектор в направлении распространения волны,
— единичный вектор в направлении распространения волны,  Дж·с.
Дж·с.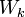
 В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов
В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов  вольт
вольт

 — циклическая частота,
— циклическая частота,  — кинетическая энергия свободной частицы,
— кинетическая энергия свободной частицы,  — полная (релятивистская) энергия частицы,
— полная (релятивистская) энергия частицы, 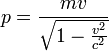 — импульс частицы,
— импульс частицы,  волны де Бройля хотя и больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).
волны де Бройля хотя и больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом). равна скорости частицы
равна скорости частицы  .Связь между энергией частицы
.Связь между энергией частицы  волны де Бройля
волны де Бройля 
 координаты и среднеквадратического отклонения
координаты и среднеквадратического отклонения  импульса, мы найдем что:
импульса, мы найдем что: ,где
,где  может быть измерен с высокой точностью, но тогда
может быть измерен с высокой точностью, но тогда  зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат еёмодуля
зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат еёмодуля  представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами
представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами  .Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями
.Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями  и
и  , то она может пребывать и в состоянии, описываемом волновой функцией
, то она может пребывать и в состоянии, описываемом волновой функцией  при любых комплексных
при любых комплексных  и
и  .
. . Это квантовое число принимает значения
. Это квантовое число принимает значения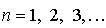 и определяет полную энергию электрона в любом квантовом состоянии
и определяет полную энергию электрона в любом квантовом состоянии .
.
 .
.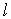 . В квантовых состояниях с заданным значением главного квантового числа
. В квантовых состояниях с заданным значением главного квантового числа  азимутальное квантовое число может иметь следующие значения:
азимутальное квантовое число может иметь следующие значения: . Из выводов предыдущего параграфа следует, что стационарные волновые функции
. Из выводов предыдущего параграфа следует, что стационарные волновые функции 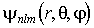 , описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии
, описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии  , но и оператора квадрата момента импульса
, но и оператора квадрата момента импульса  , причем
, причем .
.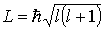 .
.
 -состояниях и, частности, в основном
-состояниях и, частности, в основном  -состоянии, когда
-состоянии, когда  , по формуле (5.38) получаем
, по формуле (5.38) получаем  .
. .
. со скоростью
со скоростью  , величина орбитального механического момента равна
, величина орбитального механического момента равна  . Если время полного оборота электрона
. Если время полного оборота электрона  , то такому движению соответствует замкнутый ток
, то такому движению соответствует замкнутый ток ,
, .
. .
.
 противоположно направлению вектора механического момента импульса
противоположно направлению вектора механического момента импульса  (рис. 5.8).Для расчета орбитального магнитного момента в квантовой теории следует определить пространственную плотность электрического тока
(рис. 5.8).Для расчета орбитального магнитного момента в квантовой теории следует определить пространственную плотность электрического тока  через плотность потока вероятностей
через плотность потока вероятностей  по формуле:
по формуле: 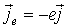 . Плотность потока вероятности при этом можно найти по формуле (3.23), зная волновую функцию электрона в заданном квантовом состоянии атома. Точный квантовомеханический расчет гиромагнитного отношения также приводит к формуле (5.39).
. Плотность потока вероятности при этом можно найти по формуле (3.23), зная волновую функцию электрона в заданном квантовом состоянии атома. Точный квантовомеханический расчет гиромагнитного отношения также приводит к формуле (5.39).
 , величина которого определяется формулой (5.38), но и магнитным моментом.
, величина которого определяется формулой (5.38), но и магнитным моментом.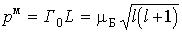 .
.

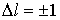 , называется правилом отбора. Наличие такого правила отбора обусловлено тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для электрона всегда на единицу.3. Магнитное квантовое число
, называется правилом отбора. Наличие такого правила отбора обусловлено тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для электрона всегда на единицу.3. Магнитное квантовое число 


