Межпопуляционные взаимоотношения и их классификация. Нейтрализм как форма взаимодействия.

 

41.Хищничество и его значение в экосистемах. Модель Лотки – Вольтерра.

 

Хищничество (+: -). Для взаимодействий типа «хищник – жертва» итальянские математики А. Лотка в 1925 г. и независимо В. Вольтерра в 1926 г. разработали первую математическую модель экологического процесса, ставшую первой подобной моделью в биологической

науке. Методологические подходы, использованные для разработки модели «хищник – жертва», стали основой для моделирования других типов межпопуляционных взаимодействий.

Отношения типа «хищник – жертва» чрезвычайно распространены в природе. Они не далеко не ограничиваются хрестоматийными примерами, такими как «волки – овцы» или «кошки – мыши». В широком смысле они охватывают все межпопуляционные взаимодействия, при которых одни организмы используют в пищу другие, при этом умерщвляя их. Поэтому к ним

также относятся такие распространенные в природе связи, как «растительноядные животные – растения», например, «дафнии – одноклеточные водоросли». Хищниками являются также киты, фильтрующие планктон, и птицы, питающиеся семенами. Целый ряд отношений, обычно включаемых в категорию «паразит – хозяин», скорее относятся к типу «хищник – жертва». Так, свободноживущие перепончатокрылые насекомые из семейства наездников (Ichneumonidae)

откладывают яйца в тела личинок и куколок других видов насекомых. Выходящие из яиц личинки используют в пищу ткани личинок и куколок и к концу развития приводят своих хозяев к гибели. Подобные виды носят название паразитоидов. Поэтому сейчас в экологии часто говорят не об отношениях «хищник – жертва», а об отношениях «потребитель – ограниченный пищевой ресурс» или «жертва – эксплуататор». В этих отношениях потребителем (эксплуататором) является гетеротрофный организм, а его жертвой, или пищевым ресурсом, –

любой другой живой организм. Однако иногда потребителем может являться даже растение, например насекомоядная росянка. Иногда, в случае каннибализма, потребитель и потребляемая им пища относятся к одному виду.

 

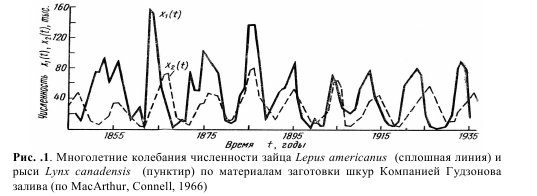
Модель Лотки – Вольтерра. Толчком к разработке этой модели стал анализ статистических данных о заготовках пушнины Компанией Гудзонова залива с конца XVIII и до середины XX века на территории современной Канады. Поскольку промысел пушнины в то время был очень интенсивным, можно считать, что количество заготовленных шкур промысловых видов

пропорционально их численности в природе. Было замечено, что численность основных объектов промысла – американского зайца-беляка Lepus americanus и охотящейся на него канадской рыси Lynx canadensis претерпевала значительные циклические колебания с периодом около 10 лет (рис.1). При этом максимумы численности хищника, как правило, наблюдались на 2–3 года позднее максимумов численности жертвы.

 

Рассмотрим простейший вариант модели Лотки – Вольтерры. В ней предполагается, что увеличение численности каждой из взаимодействующих популяций (хищника и жертвы) ограничивается только другой популяцией. Поэтому рост численности жертв лимитируется их потреблением хищниками, а рост численности хищников – недостаточным числом жертв. Принимается, что количество пищи для жертвы всегда достаточно, т. е. численность ее

популяции никогда не превышает емкость среды. Поэтому никакого самоограничения численности популяций жертвы или хищника по принципу отрицательной обратной связи модель не предполагает.

 

 

Обозначим численность популяции жертвы как N1, а популяции хищника – как N2. Допустим, численность популяции жертвы в отсутствии хищника растет экспоненциально, а пресс хищника тормозит этот рост. При этом смертность в популяции жертвы прямо пропорциональна частоте встреч хищника и жертвы, т.е. произведению плотностей их популяций. Тогда мгновенная скорость изменения численности жертвы (dN1/dt) может быть

выражена уравнением

dN1/dt = r1N1 – p1N1N2, (1)

где r1 – удельная скорость роста численности жертвы, p1 – константа, связывающая смертность жертвы с плотностью хищника. Очевидно, p1 > 0. Мгновенная скорость роста численности популяции хищника (dN2/dt) принимается равной рождаемости, которая, в свою очередь, зависит от интенсивности потребления хищников жертв и удельной скорости смертности:

dN2/dt = p2N1N2 - d2N2, (2)

где p2 – константа, связывающая удельную рождаемость в популяции хищника с плотностью жертв, d2 – удельная скорость смертности в популяции хищника. Решение системы этих уравнений позволяет определить условия поддержания постоянной, или равновесной численности хищника и жертвы. Если в (2) принять, что dN1/dt = 0, тогда r1N1 = p1N1N2. Отсюда популяция жертвы сохраняет постоянную численность, если численность популяции

хищника равна N2 = r1/p1. Аналогичным образом доказывается, что популяция хищника сохраняет постоянную численность, если численность популяции жертвы равна N1 = d2/p2.

Отложим на графике по оси абсцисс численность жертв (N1), а по оси ординат – численность хищников (N2). Тогда линии (изоклины), показывающие условия постоянства численности хищника и жертвы, представляют две прямые, перпендикулярные друг другу и координатным осям (рис. 2а). Точка их пересечения, соответствующая равной численности хищника и жертвы (N1 = N2), следует условию r1/p1 = d2/p2. При этом если численность жертвы N1 < d2/p2, то численность хищника (N2) всегда будет уменьшаться, а если N1 > d2/p2 – возрастать. Соответственно и численность жертвы возрастает, если численность хищника N2 < r1/p1, и

уменьшается – если N2 > r1/p1. Решение системы уравнений (1) и (2) позволяет получить зависимость числа хищников от числа жертв (рис. 2), или так называемый «фазовый

портрет системы». Она представляет собой окружность, центр которой образует пересечение изоклин хищника и жертвы. Образованный окружностью круг изоклины делят на четыре сектора. В первом секторе наблюдается возрастание численности хищника и жертвы, во втором – численность жертвы уменьшается, хищника - увеличивается, в третьем – уменьшение численности обоих видов, а в четвертом – уменьшение численности хищника и увеличение

численности жертвы.

 

Рис. 2. Графическая модель, показывающая возникновение устойчивых колебаний

численности хищника и жертвы. а. положение изоклин, характеризующих постоянство

численности хищника и жертвы. Стрелками показаны векторы изменения численности

хищника и жертвы. б. Циклические колебания численности хищника (пунктир) и жертвы

(сплошная линия), возникающие согласно данной модели.

 

Радиус полученного круга (R), отражающий размах колебаний численности обоих взаимодействующих видов, легко рассчитать по теореме Пифагора:

R2 = (ΔN1)2 + (ΔN2)2 (3)

Отсюда сумма квадратов изменения численности хищника и жертвы – есть величина постоянная. По (3) можно рассчитать изменения численности одного из взаимодействующих видов по изменению численности другого. Например:

ΔN1 = [ R2 – (ΔN2)2]1/2.

Если проанализировать изменения численности хищника и жертвы во времени, можно получить две синусоидальные кривые, максимумы которых сдвинуты относительно друг друга (рис.2), или так называемую «временнэю развертку». При этом на обоих кривых выделяются те же четыре фазы изменения численности взаимодействующих видов, которые выявлены на фазовом портрете системы. Такие циклы в модели Лотки – Вольтерры принято

называть устойчивыми предельными циклами.

 

Модель Лотки – Вольтерры объясняет циклические колебания численности обоих взаимодействующих популяций следующим образом. Когда численность популяции рыси незначительна, популяция зайца растет очень быстро. Однако увеличение ее численности приводит к возрастанию количества пищи для рысей, поэтому численность последних также начинает возрастать. В свою очередь, увеличение численности рысей приводило к тому, количество потребляемых ими зайцев возрастало, что приводило к резкому снижению числа

последних; затем цикл вновь повторялся. Таким образом, численность хищника и жертвы образуют регулярные циклические колебания. Регуляция численности обоих популяций осуществляется по принципу отрицательной обратной связи.

 

 

42. Паразитизм и его значение в экосистемах.

 

Паразитизм (+: -) – взаимодействие, при котором один вид (паразит) использует поверхность или внутренние части тела (органы, ткани, клетки) другого организма (хозяина) в качестве среды своего обитания и (или) источника пищи. При этом паразит наносит хозяину определенный вред, часто весьма значительный, вплоть до гибели. Среди хозяев выделяются основные, в которых паразит достигает половой зрелости и производит потомство, и промежуточные, в которых паразит проходит промежуточные стадии жизненного цикла. Часто промежуточных хозяев может быть несколько, иногда их нет вовсе. Как правило, отношения «паразит – хозяин» отличаются определенной видоспецифичностью. Большинство видов паразитов способно паразитировать на определенном виде хозяев или на небольшой группе близкородственных видов. Организм хозяина можно рассматривать как остров, население которого составляют паразиты. Возбудители заболевания могут переселяться с одного на другой только с помощью переносчиков. Чем дальше такие острова друг от друга, тем ниже вероятность передачи инфекции.

Паразиты подразделяются на две основные группы:

Микропаразиты размножаются непосредственно внутри тела хозяина, обычно внутри его клеток. К ним относятся протисты, бактерии и вирусы. Многие из них являются переносчиками опасных заболеваний.

Макропаразиты развиваются на поверхности или во внутренних полостях тела организмов. В их жизненном цикле имеются особые стадии, покидающие хозяев, чтобы заселить новых хозяев. К макропаразитам относятся плоские и круглые черви, членистоногие – вши, блохи и др.

Паразитизм очень широко распространен в биосфере, он встречается во всех царствах живых организмов. Кроме того, все вирусы являются паразитами. Многие типы целиком состоят из паразитов, например, скребни. В значительно меньшей степени паразитизм распространен среди растений, хотя паразитические растения не так уж редки, например омела, раффлезия. Полностью отсутствуют паразиты среди вторичноротых животных.

 

 

43.Внутривидовая конкуренция и компенсационный рост.

 

Если конкуренты принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией. Конкуренция между особями одного вида является наиболее острой и жесткой в природе, поскольку они имеют одинаковые потребности в экологических факторах. Внутривидовую конкуренцию можно наблюдать в колониях пингвинов, где происходит борьба за жизненное пространство. Каждая особь удерживает свой участок территории и агрессивно настроена по отношению к соседям. Это приводит к четкому разделению территории внутри популяции.

Внутривидовая конкуренция на том или ином этапе существования вида встречается почти всегда, поэтому в процессе эволюции у организмов выработались приспособления, снижающие ее интенсивность. Наиболее важные из них — способность к расселению потомков и охрана границ индивидуального участка (территориальность), когда животное защищает место своего гнездовья или определенный участок. Так, в период размножения птиц самец охраняет определенную территорию, на которую, кроме своей самки, не допускает ни одной особи своего вида. Такую же картину можно наблюдать и у некоторых рыб.

 

Компенсационный рост. Особи могут отставать в росте под воздействием различных факторов – высокой плотности, недостатка пищи, неблагоприятной температуры, воздействия метаболитов и т. п. Снятие лимитирующего фактора часто приводит к резкому ускорению роста аутсайдеров, что определяется как компенсационный рост. Его количественным показателем (Ксоmp) является отношение приростов массы их тела после (ΔW2) и до снятия (ΔW1) лимитирующего фактора, т. е. Ксоmp = ΔW2/ΔW1. Количественные аспекты компенсационного роста исследованы у легочного моллюска – большого прудовика Lymnaea stagnalis из двух водоемов (Голубев, Рощина, 2005). Новорожденные особи до возраста 74–84

суток содержались группами при плотностях от 5,7 до 28,5 экз·л-1. Затем из каждой группы отбирали выборки по 5 самых крупных (лидеры) и самых мелких (аутсайдеры) особей, которых выращивали раздельно при минимальной плотности 2,5 экз л-1 до возраста 150–160 суток. Значения Ксоmp для каждой выборки представлены на рис.8.

У особей из обоих водоемов Кcomp быстро снижаются с увеличением массы их тела при рассадке (Wi). Зависимость между Кcomp и Wi следует уравнению Кcomp = А – blgWi, где А и b – эмпирические коэффициенты. В численной форме данное уравнение для моллюсков из Крутыни имеет вид:

Кcomp = 19,33 – 6,06 lgWi,

а из Припяти:

Kcomp = 30,14 – 10,19 lgWi.

Таким образом, у L. stagnalis самым интенсивным компенсационным ростом обладают наиболее отставшие в росте особи. Чем ниже масса особей при снятии ограничивающего фактора, тем с большей скоростью происходит их компенсационный рост – «эффект сжатой пружины». С увеличением массы особей их способность к компенсационному росту постепенно утрачивается, а у половозрелых особей, достигших размеров, близких к

предельным, вообще отсутствует. Из приведенных уравнений возможно определить значения массы тела, выше которой моллюски полностью теряют способность к компенсационному росту, т.е. Wi, при которой Кcomp равно единице. Для особей из Припяти и Крутыни эти значения равны соответственно 725 и 1060 мг. Это приблизительно соответствует массе, при которой L. stagnalis достигает половой зрелости.

 

 

Рис.8. Зависимость между значениями Кcomp у выборок Lymnaea stagnalis из рек Припять (●) и Крутыня (○) от их средней массы (Wi, мг) при рассадке на группы.

В период компенсационного роста генеративный прирост особей (Рg) возрастает прямо пропорционально их соматическому приросту (Ps). При этом значения Pg у аутсайдеров оказались более высокими, чем у лидеров (рис.9). Связь между Pg и Ps следует уравнению Pg = -3,68 + 1,07·Ps.

Рg, мг сутки-1

 

Рис..9. Зависимость между среднесуточными величинами генеративного (Рg) и соматического (Ps) приростов у лидеров (●) и аутсайдеров (○) Lymnaea stagnalis при компенсационном росте. Пунктир – уровни достоверности 95 %

Таким образом, ускорение соматического роста аутсайдеров при компенсационном росте сопровождается параллельной интенсификацией их размножения. Благодаря способности к компенсационному росту аутсайдеры не являются популяционным балластом, при наступлении благоприятных условий они способны быстро достичь половой зрелости и внести значительный вклад в процесс воспроизводства популяции.

 

44.Внутривидовая конкуренция у животных. Ее математическая модель.

 

Внутривидовая конкуренция у животных. Конкурентные отношения в каждой популяции животных по-своему уникальны, тем не менее, существуют их некоторые общие закономерности. Количественным показателем их интенсивности является коэффициент конкуренции (Кс):

Кс = lg(No/Ni), (5)

где No – значение исследуемого параметра при отсутствии конкуренции, Ni – его значение при наличии конкуренции (Бигон и др., 1989). Если увеличение интенсивности внутривидовой конкуренции приводит к снижению исследуемых показателей, значения Кс для них, рассчитанные согласно (5), будут возрастать.

Для естественных популяций ограничивающим ресурсом часто становится пространство. Поэтому повышение плотности популяции, т.е. уменьшение количества пространства, приходящегося на одну особь в ней, всегда приводит к возрастанию внутривидовой конкуренции. Воздействие роста внутривидовой конкуренции, вызванной повышением плотности, на отдельные биологические параметры может быть неодинаковым. Для иллюстрации приведем данные, полученные при выращивании групп особей тепловодного легочного моллюска физелллы Physella integra от рождения и до возраста 32 суток в градиенте плотности от 50 до 2000 экз м-2 (табл. 1). По ним согласно (5) рассчитаны значения Кс для ряда показателей роста и размножения (рис. 4). В качестве No использованы значения соответствующих показателей при минимальной плотности. С увеличением плотности отмечено возрастание вариабельности особей

по массе тела, которую можно оценить по коэффициенту вариации (C.V.):

С.V. = (σ/Wm)·100 %,

где σ – стандартное отклонение (варианса) для массы тела особей в исследованной выборке, Wm – средняя масса особей. При каждой плотности выделялись небольшие группы особей (до 5–10 % от общей численности), отличающиеся резко повышенными или пониженными размерами, по сравнению с основной группой особей. Эти крайние группы можно условно назвать лидерами и аутсайдерами, а основную группу особей – середняками.

Лидерами считались те особи, масса которых превосходит значение Wm+σ, а аутсайдерами – те, масса которых ниже Wm–σ. Табл. 1. Воздействие плотности посадки на некоторые параметры роста и размножения у Physella integra в полевом эксперименте при средней температуре 30оС (по Голубеву, Нагорской, 1997)*

 

 

* условные обозначения: Wm – средняя масса особей; Wlead – средняя масса лидеров;

Wout – средняя масса аутсайдеров; C.V. – коэффициент вариации по массе тела; Ps –

среднесуточная соматическая продукция; Pg – среднесуточная генеративная продукция;

C – среднесуточный Р/B-коэффициент для соматической продукции.

 

Интенсификация внутривидовой конкуренции оказывает большее отрицательное воздействие на рост середняков и особенно аутсайдеров, чем на лидеров, что сказывается соответствующим образом на изменениях значений Кс для этих групп в градиенте плотности (рис.5). Поэтому аутсайдеры находятся под более сильным прессом конкуренции, чем лидеры,

 

Рис.5. Изменчивость коэффициентов конкуренции (Кс) для различных параметров у Physella integra. 1 – Wm; 2 – Wlead; 3 – Wout; 4 – C; 5 – Pg

 

Аналогичные эксперименты выполнены на головастиках лягушки Rana sylvatica (Wilbur, Collins, 1973). При низких плотностях гистограмма распределения особей по массе тела является вполне симметричной (рис.6).

 

Рис. 6. Гистограммы распределения по массе тела у головастиков лесной лягушки

Rana sylvatica в возрасте 50 суток, выращенных при разной начальной плотности.

 

Рост головастиков, находившихся в аквариуме при низкой плотности, замедлялся, если в него добавляли воду из аквариума, где головастиков содержали при высокой плотности. Очевидно, увеличение размерной дифференциации в одновозрастных группах растений и животных происходит по механизму положительной обратной связи.

 

У других организмов регуляторные механизмы могут быть еще более сложными. Например, у гигантских тропических креветок Macrobrachium rosenbergii, выращиваемых в проточных прудах, где метаболиты не накапливались, быстро выделялась небольшая группа самцов-лидеров, отличавшихся очень быстрым ростом. Остальные креветки росли медленно, но если лидеров удаляли, то из них быстро выделалась другая подобная небольшая группа особей и структура популяции быстро восстанавливалась (Ra’anan, Cohen, 1984). Поэтому периодическое изъятие лидеров в процессе культивирования креветок позволяет получить больший выход товарной продукции, чем однократный вылов всей популяции в конце сезона выращивания. У аквариумных рыбок замедление роста наблюдалось даже при их одиночном содержании, если в аквариуме были установлены зеркала, в которых рыбка могла видеть свое отражение.

 

45.Внутривидовая конкуренция у растений. Ее математическая модель.

 

Внутривидовая конкуренция у растений. Для популяций многих видов растений, особенно злаковых, установлено, что в широком диапазоне плотностей произведение средней плотности популяции (N) на среднюю массу одного растения (W) является приблизительно постоянной величиной, т. е. N·W = В, (1)

где В – биомасса популяции растений, или их урожай. Поэтому такая закономерность получила название закона постоянного конечного урожая. В таком случае W = В·N-1, или lgW = lgB – lgN. (2)

Отсюда логарифм средней массы одного растения снижается прямо пропорционально возрастанию логарифма плотности популяции. Поэтому угловой коэффициент линии регрессии уравнения (2), характеризующий угол ее наклона, равен –1. Некоторые примеры, иллюстрирующие закон постоянства конечного урожая, представлены на рис.1.

Общая биомасса в посевах клевера подземного Trifolium sunterraneum остается постоянной в широком диапазоне плотности посадки (рис. 1А). У однолетнего растения вульпии Vulpia fasciculata, произрастающего на песчаных дюнах, наклон линии регрессии уравнения (2) с возрастом популяции в конечном итоге приближается к -1 (рис. 1Б, В).

 

 

 

Рис. 1. Закон постоянства конечного урожая при разной плотности посадки в

разновозрастных популяциях некоторых видов растений. А. Изменение биомассы

популяций клевера подземного Trifolium sunterraneum. Б, В. Изменение средней

массы одного экземпляра вульпии Vulpia fasciculatа (из Бигон и др., 1989)

 

Закон постоянства урожая наблюдается и у некоторых видов животных. Так, c повышением плотности популяции морского брюхоногого моллюска – блюдечка Patella cochlear снижается средний размер особей; однако биомасса популяции остается постоянной в широком градиенте плотности (рис. 2).

 

 

Рис. 2. А. Зависимость среднего размера особей и биомассы популяции Patella

cochlear от ее плотности. Б. Структура микропопуляций блюдечка при разных

плотностях.

 

С другой стороны, в загущенных посевах многих видов растений, особенно имеющих развитую крону, часто наблюдается самоизреживание (рис.3), т. е. постепенное снижение по мере роста численности экземпляров на единице площади. Это обусловлено тем, что более низкие экземпляры, оказавшись в тени крон более высоких соседних растений, еще более отстают в росте и в конечном итоге погибают. В данном случае регуляция численности популяции происходит по принципу положительной обратной связи. Самоизреживание наиболее выражено в популяциях древесных растений, например, в искусственных лесопосадках ели или сосны. Для злаков самоизреживание менее характерно, особенно при достаточно низких плотностях, поскольку их колосья дают сравнительно мало тени. Для иллюстрации приведем данные экспериментов с плевелом многолетним (райграсом) Lolium perenne (Lonsdale, Watkinson, 1982). Растения высевали при пяти плотностях от 103 до 105 семян на 1 м2 на участках с разным затенением, а затем через 14, 35, 76, 104 и 146 суток после появления проростков на каждом участке определяли среднюю массу растений. При высокой освещенности (рис. 3А) наибольшее самоизреживание отмечено при двух наивысших плотностях, где оно было заметным уже после 35 суток выращивания. При минимальной плотности снижение численности когорты отмечено лишь к концу эксперимента. Снижение плотности когорты (N) приводило к увеличению средней массы одного растения (W). Траектории изменений W при любой плотности когорты направлены к единой прямой (линия самоизреживания), соответствующей уравнению:

W = cN-3/2, (3)

где с – константа, равная массе растения при плотности, равной единице.

 

 

Рис.3. Изменения численности и средней массы растений в когортах плевела

многолетнего Lolium perenne, высаженного при пяти значениях плотности семян на

1 м2: ● – 1000; ○ – 5000; ■ – 10 000; □ – 50 000; ▲ – 100 000 на участках без

затенения (А) и затененном на 83% (Б). Стрелки на линиях для каждой плотности

указывают направление траекторий изменения численности когорты и средней

массы растений в ней по направлению к линии изреживания Поскольку показатель степени в (3) равен –3/2, выявленная закономерность, отмеченная также и для многих других видов растений (рис.4), часто называется «законом трех вторых». Из него следует, что в самоизреживающейся популяции средняя масса одного растения возрастает быстрее, чем снижается их плотность.

 

 

Рис.4. Самоизреживание среди разных видов древесных и травянистых растений. Каждая линия представляет данные для отдельного вида, стрелки на них

указывают направления к общей линии изреживания, которая имеет наклон, близкий к -3/2 (по White, 1980)

При сильном затенении траектории изменения плотности и массы растений направлены к линии регрессии, имеющей наклон, равный –1 (рис.3Б), т.е. в данных условиях выполняется закон постоянства урожая.

Наиболее вероятное объяснение «закона трех вторых» заключается в следующем. Когорта растений представляет массу или объем (параметры, пропорциональные их размеру в степени 3), размещенные под улавливающей свет листовой поверхностью, имеющую некоторую площадь (параметр, пропорциональный размеру в степени 2). В растущей когорте растений индекс листовой поверхности (ИЛП, отношение суммарной площади листьев к площади поверхности почвы, покрываемой кроной) быстро перестает зависеть от общей биомассы когорты и стабилизируется на определенном уровне. Поэтому ИЛП снижается пропорционально росту ее биомассы в степени –3/2 (Бигон др., 1989). При достаточно низких ИПЛ, характерных для начального периода роста растений, чистая первичная продукция их популяций, т. е. урожай, также будет прямо пропорциональной ИПЛ, чем и обусловлен показатель степени в уравнении (2).

 

Умножив обе части уравнения (3) на N, получаем

W·N = cN-3/2·N.

Поскольку произведение WN представляет биомассу когорты (В), имеем

B = cN-1/2. (4)

Отсюда

lgB = lgc – 0,5N

Исходя из (4), общая биомасса когорты растений (или их урожай) с понижением плотности их популяции будет возрастать. Этот рост, конечно, не может продолжаться бесконечно. При плотностях популяции ниже определенного предела «закон трех вторых нарушается» и в силу вступает «закон постоянства урожая».

 

 

46.Аменсализм и его значение в экосистемах. Математическая модель аменсализма.

 

Аменсализм (0: –). К этому типу относятся межвидовые отношения самой разной природы, проявляющиеся в том, что рост численности популяции одного вида взаимодействующей пары в биоценозе оказывает отрицательное воздействие на рост численности популяции другого, но сама не испытывает ответного существенного влияния. Вид, испытывающий в данной паре отрицательное воздействие, называется аменсалом. Односторонние отрицательные взаимодействия известны как между парами видов из различных царств живых организмов – бактерий, грибов, растений и животных, так и между видами из одного царства.

 

Из взаимодействий между растениями наиболее широко известна конкуренция за свет, воду и биогенные элементы (азот, фосфор, калий, микроэлементы и т. д.), однако эти отношения в большинстве случаев носят характер внутривидовой или межвидовой конкуренции и будут рассмотрены ниже. Наряду с этим, среди взаимодействующих видов растений можно выделить пары видов, один из которых сильно подавляет рост численности другого, не испытывая с его стороны сколько-нибудь заметного ответного влияния. Чаще всего в подобных случаях имеет место аллелопатическое воздействие первого вида на второй посредством выделения в окружающую среду специфических органических ингибиторов, которые тормозят рост или препятствуют размножению и развитию других растений.

Известным примером этого являются виды растений из рода орех (Iuglans), в листьях, скорлупе и корнях которых содержится юглон (5-окси-1,4-нафтохинон). Это вещество из корней, падающих на землю листьев и скорлупы вымывается осадками в почву, где подавляет рост многих видов растений.

 

Аменсализм между микроорганизмами тесно связан с выделением ими специфических веществ – антибиотиков, отрицательно воздействующих на другие микроорганизмы (антибиоз). В случае, когда продуцент антибиотика не испытывает ответного отрицательного воздействия со стороны ингибируемого вида, можно с уверенностью утверждать о наличии аменсализма.

 

Отношения между растениями и аменсалами-микроорганизмами связаны с выделением растениями антимикробных токсинов (бактерицидов, фунгицидов и т. п.). Интересным примером этого является возрастающее ингибирование травянистой растительностью деятельности почвенных нитрифицирующих бактерий в процессе сукцессии наземных экосистем. Этим достигается сохранение связанного азота в почве, как важнейшего фактора питания растений. Не менее широко распространены и случаи, когда аменсалами являются растения, рост и развитие которых подавляют токсины, выделяемые микроорганизмами или грибками. Например, различные виды грибков рода Fusarium продуцируют соединения, вызывающие у растений нарушение водного обмена.

Аменсализм между прокариотами и животными ярко иллюстрирует цветение водоемов, когда поступающие в воду токсины, выделяемые размножающимися или отмирающими планктонными цианобактериями, приводят к массовой гибели многих видов водных беспозвоночных и рыб. Интересным примером аменсализма между животными и грибами является муравей-листорез Atta sexdens, который «выращивает» в своих гнездах грибы, используемые затем в пищу. Муравьи в особых железах вырабатывают и постоянно разбрызгивают по гнезду фенилуксусную кислоту и миркамицин. Первое из этих веществ ингибирует рост бактерий, а второе – прорастание спор тех видов грибов, которые не пригодны для своего питания. Типичным примером аменсализма между животными и растениями является вытаптывание стадами крупных растительноядных млекопитающих (слоны, копытные) травяного покрова. В результате ухудшаются условия существования не только травянистых растений, но и многих видов животных, обитающих на поверхности почвы или в почвенном покрове.

 

Математическая модель аменсализма. Один из способов количественного описания отношений аменсализма между двумя видами заключается в модификации логистического уравнения роста численности взаимодействующих популяций. Приведем данную модель в изложении В. Д. Федорова и Т. Г. Гильманова (1980). Допустим, между популяциями двух видов существуют отношения аменсализма. Тогда скорость роста численности одной из них выражается уравнением

dN1/dt = r1N1(1 – N1/K1), (1)

где r1 – максимально возможная удельная скорость роста популяции первого вида, достигаемая при ее минимальной плотности; К1 – ее предельная (максимально возможная) численность, что может являться показателем емкости для популяции нее. Предположим, что с увеличением численности первого вида (N1) уменьшается емкость среды для второго вида, т.е. аменсала. В простейшем случае это уменьшение можно выразить линейным уравнением:

К2(N1) = K2 – a21N1,

где К2(N1) – предельная численность популяции вида-аменсала, когда численность популяции первого вида достигла N1; K2 – предельная численность популяции вида-аменсала в отсутствии первого вида; a21 (читается «а два-один») – коэффициент ингибирования, показывающий, на сколько особей снижается предельная численность вида-аменсала при росте численности популяции первого вида (N1) на одну особь. Очевидно, что

a21 = [К2 – K2(N1)]/N1. (2)

Тогда скорость роста численности популяции вида-аменсала (N2) в зависимости от достигнутой численности популяции первого вида (N1) описывается уравнением:

dN2/dt = r2N2[1 – N2/(K2 – a21N1)]. (3)

Определим условия, при которых скорость роста популяции вида-аменсала, заданная (3), становится равной нулю, т.е., когда r2N2[1 – N2/(K2 – a21N1)] = 0. (4)

Поскольку значения r2 и N2 в (.4) явно не равны нулю, остается предполагать, что 1 – N2/(K2 – a21N1) = 0. Отсюда получим зависимость численности популяции вида-аменсала (N2) от численности популяции вида, взаимодействующего с ним (N1):

N2 = K2 – a21N1. (5)

Линия регрессии уравнения (16.5) на графике представляет прямую линию, или изоклину (рис.1), которая является геометрическим местом точек, представляющих такие комбинации N1 и N2, при которых удельная скорость роста популяции вида-аменсала (r2) равна нулю.

 

Рис. 1. Фазовый портрет двухвидовой системы с аменсализмом при слабом ингибировании. 1 – линия регрессии уравнения (16.5), отражающая снижение предельной численности популяции вида-аменсала с увеличением численности

популяции первого вида. 2 – линия, отражающая постоянство предельной численности популяции вида, взаимодействующего с аменсалом.

 

Легко видеть, что значение a21 соответствует тангенсу угла наклона изоклины (16.4) к оси абсцисс. Внизу и слева от изоклины при всех комбинациях N1 и N2 значения r2 для популяции вида-аменсала положительны, а сверху и справа от нее – отрицательны.

 

Аналогичным образом, приравняв к нулю (рис.1), легко убедиться, что график зависимости численности первого вида от численности вида-аменсала представляет перпендикуляр к оси абсцисс, в точке, соответствующей предельной численности первого вида, т. е. К1. Это является графической иллюстрацией положения, что изменения численности популяции вида-аменсала не оказывают никакого влияния на численность вида, взаимодействующего с ним. Справа от перпендикуляра скорость роста популяции первого вида (r1) отрицательна, а слева – положительна.

Пересечение двух прямых на графике (рис. 1) делит плоскость графика (N2 – N1) на четыре сектора (I – IV). Определим суммарные значения изменения численности обеих взаимодействующих популяций в каждом из них. В первом секторе численность популяций первого и второго видов (N1 и N2) снижается, что показано соответствующими векторами N1 и N2. Суммарную численность обеих взаимодействующих популяций (ΣN), которая также будет снижаться, можно определить по правилу сложения векторов. Суммарный вектор ΣN направлен к точке пересечения прямых на рис. 1. Аналогичным образом можно найти направления векторов ΣN в остальных секторах и убедиться, что все они также направлены к точке пересечения. Таким образом, несложный анализ системы уравнений (1) и (3) показывает, что при положительных значениях коэффициентов r1, r2, K1, K2 и a21 исход отношений между взаимодействующими видами определяется соотношениями этих коэффициентов. Существует два варианта этого исхода. В первом варианте, когда K2/K1 > a21 (слабое ингибирование) точка пересечения прямых лежит выше оси абсцисс. В этом случае возможно

единственное устойчивое состояние, при котором сосуществуют обе взаимодействующие популяции. К нему сходятся решения из любого начального состояния с положительными значениями численности обеих популяций. Нетрудно найти, что предельная численность популяции вида-аменсала снизится до уровня, равного К2 – а21К1, а первого вида, взаимодействующего с ним, – останется прежней, т. е. равной К1. Это означает, что оба взаимодействующих вида могут сосуществовать, хотя максимальная численность вида-аменсала снизится по сравнению с таковой при отсутствии взаимодействия.

Во втором случае, при K2/K1 < a21 (сильное ингибирование), точка пересечения прямых находится ниже оси абсцисс (рис. 2). В этом случае система также имеет единственное устойчивое состояние, при котором, однако, значение К2 – а21К1 является отрицательным. Из этого следует, что численность популяции вида-аменсала с увеличением численности популяции первого вида постепенно снизится до нуля, т. е. произойдет его полное вытеснение.

 

Рис. 2. Фазовый портрет двухвидовой системы при аменсализме с сильнымингибированием.

 

Результаты