
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Теоретическая механикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ Дисциплина «Основы технической механики» является важной общепрофессиональной дисциплиной, назначение которой – дать будущим техникам основные сведения о законах равновесия и движения материальных тел; о методах расчета элементов машин и сооружений на прочность, жесткость и устойчивость; об устройстве, области применения механизмов и машин общего назначения. Знания и навыки, полученные при изучении технической механики, являются основой для освоения смежных специальных дисциплин. Настоящее пособие содержит перечень учебной литературы, программу дисциплины, задания на контрольную работу и методические указания по их выполнению.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Материал программы дисциплины «Техническая механика» состоит из трех разделов: теоретическая механика, основы сопротивления материалов, детали машин и механизмов. Каждый раздел технической механики необходимо изучить, затем выполнить контрольную работу. Изучение учебного материала следует вести в последовательности: -ознакомиться с содержанием программы, подобрать учебную литературу; -изучить материал каждой темы задания; -ответить на вопросы для самопроверки; -закрепить усвоение материала путем разбора решенных задач, приведенных в учебной литературе. После того как материал изучен, можно приступить к выполнению контрольной работы. Контрольная работа выполняется по одному из 30 вариантов. Варианты для каждого студента – индивидуальные. Номер варианта определяется порядковым номером в журнале группы. При выполнении контрольных работ необходимо соблюдать следующие требования: -каждая контрольная работа выполняется в отдельной тетради; -на обложку тетради приклеивается заполненный студентом бланк «Контрольная работа»; -контрольная работа выполняется чернилами, разборчивым почерком, с интервалом между строками, а рисунки и схемы - карандашом с соблюдением правил черчения; для пометок и замечаний преподавателя необходимо оставлять поля, а в конце работы – несколько страниц для рецензии; -каждую задачу нужно начинать с новой страницы, тексты условий задач переписывать полностью; -решение задач сопровождать краткими пояснениями, в которых указывать, какая величина определяется, по какой формуле (привести эту формулу в общем виде), какие величины подставляются в формулу; -вычисления в задачах контрольной работы производить в единицах СИ, применять стандартные символы для обозначения величин; при всех исходных и вычисленных величинах должны указываться единицы измерения (размерности); -ответы на контрольные вопросы необходимо давать сжато, конкретно, по существу заданного вопроса; -в конце контрольной работы следует указать список использованной литературы (наименование, автор, год издания). Перед чистовым оформлением задачи тщательно проверить правильность всех вычислений, оценить правдоподобность полученных результатов. Выполненную работу следует подписать, поставить дату и своевременно выслать в колледж. После получения зачтенной работы необходимо внимательно изучить рецензию и все замечания преподавателя, обратить внимание на ошибки и доработать материал. Не зачтенная работа выполняется заново или переделывается частично по указанию преподавателя. При затруднениях в решении задач контрольной работы можно обратиться к преподавателю колледжа с просьбой о консультации по неясным вопросам. Работа, выполненная не по своему варианту или не в полном объеме, проверке не подлежит и возвращается без оценки. ЛИТЕРАТУРА 1. Мовнин М.С., Израелит А.Б., Рубашкин А.Г. Основы технической механики. Санкт-Петербург, «Политехника», 2003. 2. Эрдеди А.А., Эрдеди Н.А., Теоретическая механика. Сопротивление материалов. Москва, «Высшая школа», 2001. 3. Эрдеди А.А., Эрдеди Н.А., Детали машин, Москва, «Высшая школа», 2001. ПРОГРАММА ВВЕДЕНИЕ Значение дисциплины, ее связь с другими изучаемыми дисциплинами. Роль технической механики в технике. Краткий обзор развития технической механики. Разделы технической механики.
Тема 1.1. Основные понятия и аксиомы статики Абсолютно твердое тело. Материальная точка, система материальных тел. Свободное и несвободное тела. Сила как вектор. Система сил, эквивалентные системы сил. Силы внешние и внутренние. Условия равновесия твердого тела. Правило параллелограмма сил. Связи, реакции связей. Аксиомы статики. Тема 1.3. Пара сил Понятие о паре сил. Момент пары, знак момента. Основные свойства пар сил. Условие равновесия плоской системы пар сил. Тема 1.6. Центр тяжести Центр параллельных сил, его свойства. Формулы для определения координат центра параллельных сил. Силы тяжести. Центр тяжести как центр параллельных сил. Определение координат центра тяжести простых и сложных сечений. Тема 1.7. Основы кинематики Основные понятия: пространство и время, механическое движение. Параметры движения и способы его задания. Классификация видов движения точки и тела. Уравнения движения, скорость и ускорение точки при естественном способе задания движения. Виды движения точки в зависимости от ускорения. Равнопеременное движение точки. Поступательное движение твердого тела и его свойства. Вращательное движение твердого тела. Угловая скорость, частота вращения. Угловое ускорение. Линейные скорости точек вращающегося тела. Нормальное, касательное и полное ускорения. Выражение нормального и касательного ускорений точки через угловую скорость и угловое ускорение тела. Тема 1.8. Основы динамики Основные понятия, законы динамики. Сила инерции несвободной материальной точки. Касательная и нормальная составляющие силы инерции при криволинейном движении точки (принцип Даламбера). Работа постоянной силы при прямолинейном движении. Работа сил тяжести. Мощность. Единицы работы и мощности в Международной системе (СИ). Понятие о механическом коэффициенте полезного действия. Работа и мощность при вращательном движении тела. Тема 2.3. Срез и смятие Понятие о срезе и смятии. Основные расчетные предпосылки и формулы, условности расчета. Допускаемые напряжения на срез и смятие. Расчеты на срез и смятие болтовых и сварных соединении. Тема 2.5. Прямой изгиб Основные понятия и определения. Классификация видов изгиба. Внутренние силовые факторы при прямом изгибе. Дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом. Построение эпюр поперечных сил и изгибающих моментов, Зависимость между изгибающим моментом и кривизной оси балки. Жесткость сечения при изгибе. Нормальные напряжения в поперечных сечениях балки. Расчеты на прочность при изгибе. Рациональные формы поперечных сечений балок. Тема 2.6. Кручение Понятие о сдвиге. Закон Гука для сдвига. Модуль сдвига. Зависимость между упругими постоянными для тела (без вывода). Кручение бруса круглого поперечного сечения. Крутящий момент, построение эпюр крутящих моментов. Основные гипотезы. Напряжения в поперечных сечениях бруса, угол закручивания. Полярные моменты инерции и сопротивления для круга и кольца. Расчеты валов на прочность и жесткость. Рациональные формы поперечных сечений валов. Тема 2.7. Изгиб с кручением Работа бруса при совместном действии изгиба и кручения. Внутренние силовые факторы и напряжения в поперечном сечении. Эквивалентный момент. Формулы для определения эквивалентного напряжения по гипотезам наибольших напряжений и энергии формоизменения. Расчет валов на изгиб с кручением. РАЗДЕЛ 3. ДЕТАЛИ МАШИН Тема 3.1. Основные положения Цели и задач раздела "Детали машин". Основные определения, механизм и машина. Классификация машин. Современные тенденции в развитии машиностроения. Требования к машинам и деталям машин. Основные критерии работоспособности и расчета деталей машин, прочность и жесткость. ЗАДАНИЕ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
ЗАДАЧА 1 (рис.1). Однородная стрела АВ настенного крана весом 2 кН, несущая груз весом 10 кН, удерживается в равновесии тросом СD. Приняв АВ = 3 м и ВС = 1 м, определить реакции опорного шарнира А и силу натяжения троса СD.
ЗАДАЧА 2 (рис.1). Неподвижно зажатый опорный столб АВ нагружен силой 2, 5 кН. Приняв АВ = 5 м и АС = CD = 1,5 м, определить опорные реакции в точках А, С и D. Весом столба, а также трением пренебречь.
ЗАДАЧА 3 (рис.1). Стоящий наклонно однородный щит АВ весом 400 Н удерживается в равновесии веревкой АD. Пренебрегая трением и приняв АВ = 6 м, ВС = 1 м, определить опорные реакции в точках А и С и силу натяжения веревки.
ЗАДАЧА 4 (рис.1). Однородная плита АВ односкатной крыши весом 20 кН испытывает ветровую нагрузку F = 5 кН, приложенную в точке С горизонтально. Приняв АВ = 9 м, АС = CВ, определить опорные реакции в точках А и В. ЗАДАЧА 5 (рис.1). Натяжное устройство представляет собой двуплечий рычаг АВС, одно плечо которого несет груз весом 500 Н, а другое плечо служит для натяжения троса. Приняв АВ = 0,2 м и ВС = 0,5 м, определить реакции опорного шарнира В и силу натяжения троса. Весом рычага пренебречь.
ЗАДАЧА 6 (рис.1). Однородная плита АВ весом 3 кН удерживается в равновесии в горизонтальном положении с помощью трех стержней. Приняв АВ = 6 м и АС = 2 м, определить силы, нагружающие стержни.
ЗАДАЧА 7 (рис.1). Однородную плиту АВ весом 4 кН равномерно вытягивают из приямка с помощью барабанной лебедки D. Приняв АВ = 10м и ВС = 2 м, определить для данного положения плиты опорные реакции в точках А и С и силу натяжения троса ВD. Трением пренебречь.
ЗАДАЧА 8 (рис.1). Поворотный однородный рычаг АВ с помощью растянутой пружины силой упругости 5 Н прижат к вращающейся кулачковой шайбе в точке С. Приняв АD = 100 мм, DС = 80 мм, определить реакции опорного шарнира А и силу давления рычага на кулачок. Весом частей механизма, а также трением пренебречь.
ЗАДАЧА 9 (рис.1). Однородная лестница АВ весом 200 Н опирается на пол и стены приямка. В точке С на лестнице стоит человек весом 700 Н. Приняв АВ = 5 м и АС = 3 м, определить опорные реакции в точках А и В. Трением пренебречь.
ЗАДАЧА 10 (рис.1). Однородная стрела АВ подъемного крана весом 8 кН, несущая на своем конце груз весом 40 кН, удерживается в равновесии с помощью троса СD барабанной лебедки D. Приняв АВ = 5 м и ВС = 2 м, определить реакции опорного шарнира А и силу натяжения троса СD.
ЗАДАЧИ 11-20 (рис.2). Для тонкой однородной пластины, размеры которой заданы в миллиметрах, определить положение центра тяжести.
ЗАДАЧИ 21-30 (рис. 3, табл. 2). Двухступенчатый стальной брус нагружен силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Сделать вывод о прочности бруса, приняв [σ] =160МПа. Определить удлинение (укорочение) бруса, приняв Е=2∙10 МПа.
Таблица 2
ЗАДАЧИ 31–35 (рис.4, табл. 3). Определить диаметр вала в опасном сечении из условия прочности, если допускаемое напряжение на кручение [τ] =100 МПа. Передаваемые на вал мощности Р1, Р2, Р3, Р4; вал вращается с угловой скоростью ω. ЗАДАЧИ 36–40 (рис.4, табл. 3). Проверить вал в опасном сечении на прочность при деформации кручения, если допускаемое напряжение [τ] =100 МПа. Передаваемые на вал мощности Р1, Р2, Р3, Р4; вал вращается с угловой скоростью ω.
Таблица 3
ЗАДАЧИ 41 – 50 (рис. 5, табл. 4). Для двухопорной стальной балки определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и подобрать необходимые размеры поперечного сечения заданной формы, приняв [σи] = 150МПа для балки из стали и [σи] =12МПа для деревянной балки. Таблица 4
ЗАДАЧИ 51 – 60 (рис. 6, табл. 5). Привод состоит из электродвигателя мощностью Рдв с угловой скоростью вала ω дв и двухступенчатой передачи, включающей редуктор и открытую передачу, характеристики звеньев которой заданы (d и z). Угловая скорость выходного вала ω вых. Требуется определить: -передаточное отношение привода и передаточное число редуктора; -общий коэффициент полезного действия (КПД) всего привода; -мощности на вала; - угловые скорости валов; - вращающие моменты на каждом валу привода. Таблица 5
К ЗАДАЧАМ 1-10 К решению этих задач следует приступить после изучения тем «Основные понятия и аксиомы статики», «Плоская система сходящихся сил», «Пара сил», «Плоская система произвольно расположенных сил». При этом необходимо усвоить понятия «проекция силы на ось», «момент силы относительно точки», научиться составлять уравнения равновесия для плоской системы сил. Во всех задачах определению подлежат опорные реакции тела, находящегося в равновесии под действием плоской системы произвольно расположенных сил. Реакции в стержнях направлены вдоль стержней, реакция гибкой связи направлена вдоль связи, реакции плоскости направлены перпендикулярно плоскости. Реакция шарнирно-подвижной опоры направлена по нормали к опорной поверхности шарнира. Реакцию шарнирно-неподвижной опоры принято представлять в виде двух составляющих реакций по осям координат. Вид применяемой системы уравнений равновесия может быть различным Σ МА = 0, Σ МВ = 0, Σ X = 0, Σ Y = 0. Три из этих уравнений используются для решения, одно из них – для проверки решения. При составлении уравнений следует помнить, что проекция силы на ось численно равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси ([1], §7). Моментом силы относительно точки называется произведение модуля силы на плечо; плечом силы является перпендикуляр, опущенный из точки, относительно которой берется момент, на линию действия силы. Если при этом сила стремится повернуть тело по часовой стрелке, то ее момент считают положительным, если против часовой стрелки – отрицательным ([1], §15). ПРИМЕР 1. Однородная балка, сила тяжести которой равна 2 кН, закреплена в точке А с помощью шарнирно-неподвижной опоры и опирается в точке В на ребро стены (рис. 7а). Найти реакции опор, если АС = 4м, ВС = 1м. Решение
Рис. 7 На балку действует одна активная сила – сила тяжести. В силу однородности балки сила тяжести приложена в ее середине, т. е. в точке D. Освободим балку от связей, приложив к ней вместо связей силы реакций (рис. 7б). В точке А к балке надо приложить неизвестные две взаимно перпендикулярные силы RА х и RАу. В точке В балка опирается на ребро, следовательно, реакция R В перпендикулярна балке АС (рис. 7 б). Сила тяжести вместе с реактивными силами представляет уравновешенную систему сил, произвольно расположенных в плоскости, для которой можно составить три независимых уравнения равновесия: два уравнения проекций и одно уравнение моментов. Составим уравнения равновесия: 1 ) Σ Fiх= 0. RАх – RВ cos 60 º = 0. 2 ) Σ Fiy= 0. RАу – G + RВ cos 30 º=0. Для составления уравнения моментов в качестве центра моментов может быть выбрана точка плоскости, но для получения более простого уравнения нужно в качестве центра моментов выбрать ту точку, через которую проходит большее число неизвестных сил. 3)
Из (1) Из (2)
Для проверки правильности решения воспользуемся уравнением моментов относительно точки D.
Следовательно, задача решена правильно.
К ЗАДАЧАМ 11-20 К решению задач следует приступить после изучения темы «Центр тяжести» ([1], §§ 23, 24). Центром тяжести тела называется центр параллельных сил тяжести всех элементарных частиц тела. Если тело имеет ось симметрии, то центр тяжести лежит на этой оси. Если тело имеет две оси симметрии, то центр тяжести находится на их пересечении. Центр тяжести может лежать и вне тела. Задачи решаются в следующей последовательности: 1.Составная фигура делится на простейшие геометрические фигуры, положения центра, тяжести которых известны (круг, прямоугольник, треугольник). 2.Выбирают оси координат, относительно которых берутся координаты центров тяжести каждой простейшей фигуры. 3.Вычисляют координаты центра тяжести сложной фигуры по формулам:
где
Если сечение имеет отверстия, площади отверстий вычитаются.
ПРИМЕР 2. Для тонкой однородной пластины, форма которой и размеры в миллиметрах заданы на рис.8, определить положение центра тяжести.
Рис. 8 Решение 1.Выбираем оси координат так, чтобы фигура была расположена в первом квадранте. 2. Разбиваем фигуру на три части: два прямоугольника I и II и круглое отверстие III. 3. Определяем координаты центров тяжести простейших фигур: х 1= 25 мм, y1=15мм, х 2= 40 мм, y2=50мм, (х 2 = 50 – 20/2 = 40, y2 = 30 + 40/2 = 50), х 3= 20 мм, y3=10мм. 4. Определяем площади составных частей: А 1 = 50 ∙ 30 = 1500 мм 2, А 2 = 20 ∙ 40 = 800 мм 2, А 3 = 3,14 ∙ 52 /4 = - 19,6 мм 2.
Знак «минус» означает, что А 3 - площадь отверстия. 5. Вычисляем координаты центра тяжести всей фигуры:
6. Покажем положение центра тяжести всей фигуры на чертеже: х С = 30,3 мм; yС = 28,2мм.
К ЗАДАЧАМ 21-50
Приступить к решению этих задач следует после изучения основных положений раздела «Сопротивление материалов» ([1], §§28- 1). Для успешного решения задач необходимо получить четкое представление о методе сечения для определения внутренних силовых факторов, о видах нагружения бруса, напряжениях, условии прочности и видах расчетов на прочность. В общем случае нагружения тела внутренние силовые факторы, возникающие в поперечном сечении нагруженного бруса, включают в себя продольную N z и поперечные силы Qx и Q y, а также крутящий М z и изгибающие моменты Мx, Мy. Метод сечения складывается из нескольких последовательных действий: - рассекают тело мысленно плоскостью на две части; - отбрасывают одну часть; - заменяют действие отброшенной части внутренними силовыми факторами; - уравнения равновесия составляют для оставленной части и решают, определяя из них значения и направления внутренних силовых факторов. Для наглядного изображения распределения внутренних силовых факторов вдоль оси бруса строят диаграммы, называемые эпюрами. Численное значение внутренних сил, приходящихся на единицу площади поперечного сечения у какой-либо его точки, называется напряжением. Напряжение измеряют в паскалях (1Па=1Н/мм2), кратные единицы – мегапаскаль (1МПа = 106 Па = 1Н/мм2). С помощью метода сечений определяют значение и знак внутренних силовых факторов во всех случаях по длине бруса, строят их эпюры и отыскивают опасное сечение бруса. Внутренний силовой фактор в произвольном поперечном сечении бруса численно равен алгебраической сумме соответствующих нагрузок, действующих на оставленную для рассмотрения часть бруса. Установленное в статике для сил и моментов правило знаков при определении внутренних силовых факторов неприменимо. Для каждого вида внутренних силовых факторов устанавливается собственное правило знаков. При построении эпюры любого внутреннего силового фактора должно соблюдаться следующее общее правило, вытекающее из метода сечений: внутренний силовой фактор в сечении, в котором приложена соответствующая сосредоточенная нагрузка, изменяется «скачком» на значение этой нагрузки. По виду внутреннего силового фактора устанавливают вид напряжения, возникающего в точках опасного поперечного сечения, закон его распределения по сечению и вид геометрической характеристики прочности сечения. Расчетное напряжение определяют как отношение внутреннего силового фактора к геометрической характеристике прочности. По эпюре определяют опасное сечение бруса и производят расчет на прочность. Условием прочности при расчете по допускаемому напряжению называют неравенство: σ ≤ [σ] или τ ≤ [τ], где [σ] и [τ] - допускаемое напряжение, зависящее от механических характеристик материала бруса и принятого коэффициента запаса прочности; σ и τ - расчетное напряжение. Из условия прочности определяют требуемое значение искомой величины. К решению ЗАДАЧ 21-30 следует приступить после изучения темы «Растяжение и сжатие» ([1], гл. VII). Растяжением (сжатием) называют такой вид нагружения бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор - продольная сила N, численно равная в любом поперечном сечении алгебраической сумме внешних сил, действующих на оставленную часть бруса: N = ΣFi. Продольные силы N, соответствующие деформации растяжения (т.е. направленные от сечения или от объекта равновесия) считаются положительными, в противном случае они - отрицательные. Для определения нормальных напряжений σ в поперечных сечениях значение продольных сил необходимо разделить на площади соответствующих сечений: σ = N / А. Проверка прочности осуществляется по формуле: σ = N / А ≤ [σ], где σ -наибольшее рабочее напряжение; [σ] – допускаемое напряжение для материала стержня. Превышение рабочего напряжения по сравнению с допускаемым не должно быть больше 5%. Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука: Δ l = N· l / (А· Е) = σ·ℓ / E; где Е - модуль упругости материала бруса (для стали принимают Е = 2 ∙ 105 МПа). Для бруса, имеющего несколько участков, отличающихся размерами поперечного сечения или величиной продольной силы, изменение длины всего бруса будет равно алгебраической сумме удлинений (укорочений) отдельных участков: Δ l = Σ Δ li.
ПРИМЕР 3. Для двухступенчатого стального бруса (рис. 9) построить эпюры продольных сил и нормальных напряжений. Проверить брус на прочность. Определить перемещение свободного конца бруса, приняв модуль продольной упругости Е = 2 ∙ 105 Н/мм2; F1 = 30кН; F2 = 38 кН; F 3 = 42кН; А1 = 190 мм2; А2 = 310 мм2; [σ] = 160 МПа.
Рис.9
Решение 1.Отмечаем участки, как показано на рис.9а. 2.Определяем значение продольной силы N на участках бруса: N1 =0; NII = F1 = 30 кН; NIII = F1 = 30 кН; NIV = F1 – F2 = 30 – 38 = – 8 кН; NV = F1 – F2 – F3 = 30 – 38 – 42 = – 50 кН; Строим эпюру продольных сил (рис.9б). 3. Вычисляем значения нормальных напряжений: σI = N1 / А1 = 0; σII = N1I / А1 = 30·103/ 190 = 158 Н/мм2; σIII = N1II / А2 = 30·103/ 310 = 96,8 Н/мм2; σIV = N1V / А2 = – 8·103/ 310 = – 25,8 Н/мм2; σV = NV / А2 = – 50·103/ 310 = – 161 Н/мм2; Строим эпюру нормальных напряжений (рис. 9в). 4. Проверяем прочность наиболее нагруженного участка. Условие прочности при растяжении, сжатии - σ = N / А ≤ [σ]. Наибольшее абсолютное значение рабочего напряжения возникает в пределах пятого участка. σ = σV = 161 Н/мм2 = 161 МПа; 161 МПа > 160 МПа – имеет место перегрузка бруса, которая составляет:
5.Определяем перемещение свободного конца бруса: Δ ℓ = Δ ℓ I +Δ ℓ II +Δ ℓ III+ Δ ℓ IV +Δ ℓ V; Δ ℓ = σ· ℓ / E; Δ ℓ I = σI ℓ ·I / E = 0; Δ ℓ II = σII· ℓ II / E = 158 · 0,5 · 103 / 2·105 = 0,394 мм; Δ ℓ III = σIII· ℓ III / E = 96,8 · 0,1 · 103 / 2·105 = 0,0484мм; Δ ℓ IV = σIV· ℓ IV / E = – 25,8 · 0,4 · 103 / 2·105 = – 0,0516мм; Δ ℓ V = σV· ℓ V / E = – 161 · 0,2 · 103 / 2·105 = – 0,161мм. Δ ℓ = 0,394 + 0,0484 – 0,0516 – 0,161 = 0,23 мм. Брус удлиняется на 0,23 мм. К решению ЗАДАЧ 31-40 следует приступить после изучения темы «Кручение» ([1], гл. IX). Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент Мк. Крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних моментов, действующих на оставленную часть, Мк = Σ Мi (имеется в виду, что плоскости действия всех внешних моментов перпендикулярны продольной оси бруса). Крутящий момент считают положительным, если внешний момент направлен по ходу часовой стрелки при взгляде со стороны проведенного сечения. Условие прочности при кручении: τк = Мк / Wp ≤ [τк ], где τк - рабочее напряжение, возникающее в брусе; Мк - крутящий момент на брусе; Wp - полярный момент сопротивления, зависящий от геометрических параметров бруса. Для круглого сечения можно принять Wp= 0,2 d 3 мм 3; [ τк ] - допускаемое напряжение при кручении, зависящее от материала элемента конструкции. ПРИМЕР 4. Определить диаметр вала (рис.10) в опасном сечении из условия прочности на кручение, если допускаемое напряжение на кручение [τк] =100 Н/мм2; передаваемые мощности на вал: Р1 = 8 кВт, Р2 = 4 кВт, Р3 = 3кВт, Р4 = 1 кВт. Вал вращается равномерно с угловой скоростью ω = 3 рад/с.
Рис. 10
Решение 1.Определяем вращающие моменты на шкивах: М1= Р1/ω = 8 ·103 / 3 =2666 Н·м, М2= Р2/ω = 4 ·103 / 3 =1333 Н·м, М3= Р3/ω = 3 ·103 / 3 =1000 Н·м, М4= Р4/ω = 1 ·103 / 3 =333 Н·м, здесь Р - в Вт, ω -в рад/с, М – в Н·м. Так как вал находится в равновесии, то
2.Строим эпюру крутящих моментов, разделив вал на участки. Границы участков – места приложения вращающих моментов. Используя метод сечения, определяем крутящие моменты на каждом участке: Мк1 = М к5 = 0, Мк2 = – М2 = – 1333 Н·м, Мк3 = – М2 – М4 = – 1333 –333 = – 1666 Н·м, Мк4 = – М2 – М4 + М1 = – 1333 –333 + 2666 = 1000 Н·м, или Мк4 = М3 = 1000 Н·м. Из эпюры видно, что самый опасный участок – участок 3, где Мк3 = 1666 Н·м = 1,67 кН·м 3.Из условия прочности на кручение определяем диаметр вала в опасном сечении:
Принимаем d=45мм. Остальные участки вала можно сделать меньших диаметров. К решению ЗАДАЧ 41-50 следует приступить после изучения темы «Изгиб» ([1], гл. X). При изгибе в поперечных сечениях балок возникают два внутренних силовых фактора: изгибающий момент Ми и поперечная сила Q. При определении внутренних сил учитываются как активные внешние силы, действующие на балку, так и реакции связей. Поперечная сила, возникающая в каком-либо поперечном сечении, численно равна алгебраической сумме проекций на ось y внешних сил, действующих на балку по одну сторону от рассматриваемого сечения: Q = Σ Fн, а изгибающий момент – алгебраической сумме моментов внешних сил относительно центра тяжести сечения: Ми = Σ Мi. Поперечная сила считается положительной, если внешние силы слева от сечения направлены вверх, а справа от сечения – вниз. Поперечная сила считается отрицательной, если внешние силы слева от сечения направлены вниз, а справа от сечения – вверх. Изгибающий момент считают положительным, если внешняя сила, расположенная слева от сечения, вращает относительно центра тяжести сечения по ходу часовой стрелки, а справа от сечения – против хода часовой стрелки. В противном случае момент считают отрицательным.
Рис. 11 Балки выполняют постоянного по длине поперечного сечения, поэтому его размеры подбирают только для опасного сечения, имеющего по абсолютному значению максимальный изгибающий момент. Для определения опасного сечения строят эпюру изгибающих моментов, используя метод сечений. Условие прочности при изгибе: σ и = где σ и – рабочее напряжение, возникающее в балке; М и мах - максимальный изгибающий момент; Wx - осевой момент сопротивления изгиба зависит от геометрических параметров балки. Круг диаметром d : Wx = 0,1 d3; прямоугольник (рис. 12): Wx = |




 50
50





 где
где 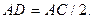
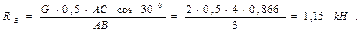

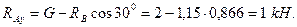






 - координаты центров тяжести простейших фигур;
- координаты центров тяжести простейших фигур; - площади простейших фигур.
- площади простейших фигур.




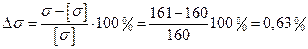 , что вполне допустимо.
, что вполне допустимо.
 . М1 – М2 – М3 – М4 = 2666 – 1333 – 1000 – 333=0.
. М1 – М2 – М3 – М4 = 2666 – 1333 – 1000 – 333=0.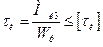 где Wр = 0,2 d3. Следовательно
где Wр = 0,2 d3. Следовательно .
.
 ≤ [σи],
≤ [σи],


