
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы и средства защиты информацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Разграничение доступа к ресурсам АСОИ Политика безопасности. Классификация политик безопасности Под политикой безопасности понимается совокупность норм и правил, регламентирующих процесс обработки информации, выполнение которых обеспечивает защиту от заданного множества угроз и составляет необходимое (а иногда и достаточное) условие безопасности компьютерной системы [1]. Основная цель создания политики безопасности информационной системы – это определение условий, которым должно подчиняться поведение подсистемы безопасности. Наиболее исследованными на практике моделями безопасности являются модели, защищающие информацию от нарушения свойств конфиденциальности и целостности. Эти модели могут быть на верхнем уровне подразделены на два больших класса – формальные модели политик безопасности и неформальные модели. Возможная классификация моделей политик безопасности представлена на рис. 2.1.
Рис. 2.1. Классификация моделей политик безопасности Формальные модели политик безопасности позволяют описать поведение подсистемы безопасности в рамках строгих математических моделей, правил. С их помощью можно доказать безопасность системы, опираясь при этом на объективные и неопровержимые постулаты математической теории. Формирование данных политик предполагает выработку критерия безопасности системы и проведение формального доказательства соответствия системы этому критерию при соблюдении установленных правил и ограничений. Неформальные модели политик безопасности предполагают описание поведения подсистемы безопасности в рамках вербальных (словесных) утверждений, не обладающих математической строгостью. Утверждения в неформальных моделях, как правило, формируют требования к поведению подсистемы безопасности на общем уровне без указания особенностей их реализации. Достоинством формальных моделей является их математическая строгость и возможность формального доказательства того, что система, находящаяся в безопасном состоянии, не может перейти в небезопасное состояние при соблюдении всех установленных правил и ограничений. Недостатком формальных моделей является их большая абстрактность, что, зачастую, не позволяет использовать правила данных моделей ко всем субъектам и объектам компьютерной системы.
Пример 2.1 Пусть для компьютерной системы задано 4 субъекта доступа S ={Administrator, User1, User2, Guest} и 5 объектов O ={FILE1.DAT, FILE2.TXT, FILE3.TXT, CD-ROM, FDD}. Множество атрибутов безопасности определено как A ={NONCONFIDENTIAL, CONFIDENTIAL, SECRET, TOP SECRET}. Пусть уровни конфиденциальности объектов определены следующим образом: FDD – NONCONFIDENTIAL. CD-ROM – CONFIDENTIAL. FILE1.DAT – SECRET. FILE2.TXT – SECRET. FILE3.TXT – TOP SECRET. Пусть уровни допуска субъектов определены следующим образом: Administrator – TOP SECRET. User1 – SECRET. User2 – CONFIDENTIAL. Guest – NONCONFIDENTIAL. Тогда, согласно правилам исходной мандатной модели: субъект Administrator будет иметь допуск ко всем объектам; субъект User1 будет иметь допуск к объектам FDD, CD-ROM, FILE1.DAT, FILE2.DAT; субъект User2 будет иметь допуск к объектам FDD, CD-ROM; субъект Guest будет иметь допуск только к объекту FDD. Однако, злоумышленник, в качестве которого возьмем субъекта Guest, завербовав пользователя User1 сможет получить доступ к информации из объекта FILE1.DAT, если User1 запишет эту информацию в объект FDD, что будет ему разрешено. Политика безопасности Белла-ЛаПадулы (БЛМ) устраняет данный недостаток исходной мандатной политики безопасности и осуществляет контроль доступа субъектов 1. Правило NRU (нет чтения вверх). Согласно данному правилу субъект 2. Правило NWD (нет записи вниз). Согласно данному правилу субъект
Рис. 2.2. Демонстрация правил политики безопасности Белла-ЛаПадулы Введение свойства NWD разрешает проблему программных закладок, так как запись информации на более низкий уровень безопасности, типичная для них, запрещена. Пример 2.2 Рассмотрим пример компьютерной системы, введенной в примере 2.1. При ее реализации в рамках политики БЛМ возможно выполнение следующих операций:
1. субъект Administrator будет иметь допуск по чтению из всех объектов, и допуск по записи в объект FILE3.TXT; 2. субъект User1 будет иметь допуск по чтению из объектов FDD, CD-ROM, FILE1.DAT, FILE2.DAT и допуск по записи в объекты FILE1.DAT, FILE2.TXT, FILE3.TXT; 3. субъект User2 будет иметь допуск по чтению из объектов CD-ROM, FDD и допуск по записи в объекты FILE1.DAT, FILE2.TXT, FILE3.TXT, CD-ROM; 4. субъект Guest будет иметь допуск по чтению из объекта FDD и допуск по записи во все объекты. Пример 2.3 Любому печатному изданию (журналы, газеты и т.п.) можно присвоить негласный уровень контроля достоверности публикуемой информации, характеризующий то, насколько хорошо проверяется достоверность публикуемой в издании информации перед ее печатью. В данном случае множество уровней контроля достоверности может быть определено следующим образом: A ={желтая пресса, нестрогий контроль, строгий контроль, совершенно строгий контроль}. Перепечатка информации из одного издания в другое может восприниматься как чтение и запись данной информации. В этом случае, перепечатка информации должна подчиняться правилам мандатной политики безопасности Биба – информация из желтой прессы не может быть напрямую перепечатана в печатном издании с совершенно строгим контролем публикуемой информации без прохождения дополнительных проверок на достоверность. Модель понижения уровня субъекта заключается в небольшом ослаблении правила чтения снизу. В данной модели субъекту разрешается осуществлять чтение снизу, но в результате такого чтения уровень целостности субъекта понижается до уровня целостности объекта. Мотивом для введения такого правила может являться то, что субъекты с высокой целостностью рассматриваются как “чистые”. Когда к чистому субъекту попадает информация из менее чистого источника, субъект “портится”, и его уровень целостности должен быть соответственно изменен. Модель понижения уровня объекта ослабляет правило для записи наверх. В данной модели субъекту разрешается записывать информацию наверх, но при этом снижается уровень целостности объекта до уровня целостности субъекта, осуществлявшего запись. Мотивы для такого правила те же, что и в модели понижения уровня субъекта. Модель контроля целостности Кларка-Вилсона. Модель контроля целостности Кларка-Вилсона (КВМ), в отличие от политики Биба является неформальной. Созданию этой модели способствовал анализ методов управления коммерческими организациями целостностью своих бумажных ресурсов в неавтоматизированном офисе, то есть был рассмотрен ряд хорошо известных методов учета целостности информационных ресурсов и сделана попытка распространения их на случай компьютерных приложений. Получившаяся модель целостности представляет собой руководство разработчикам и проектировщикам компьютерных систем для обеспечения целостности определенных вычислительных ресурсов. Модель КВМ выражается в терминах конечного множества обрабатываемых данных D. Создатели модели разделили D на два непересекающиеся подмножества, которые называются ограниченными элементами данных (CDI) и неограниченными элементами данных (UDI), при этом D = CDI È UDI, CDI ∩UDI = Æ Субъекты включены в КВМ как множество компонентов, которые могут инициировать так называемые процедуры преобразования (ПП). Процедура преобразования определяется как любая ненулевая последовательность элементарных действий (чтение, запись и т.д.). Например, субъекты могут устранять элементы данных, изменять информацию в элементах данных, копировать их и т.д.
Модель КВМ можно рассматривать как набор, состоящий из следующих девяти правил. Правило 1. В системе должны существовать особые процедуры преобразования IVP, утверждающие целостность любого CDI. Можно представить себе IVP как некий тип процедуры проверки для утверждения целостности каждого CDI и подтверждения отсутствия целостности каждого UDI. Простейшим примером такой процедуры утверждения является проверка контрольной суммы. Различия в контрольных суммах сигнализируют о внесении изменений. Правило 2. Применение любой ПП к любому CDI должно сохранять целостность этого CDI. Это правило можно рассматривать как свойство скрытия применения ПП над CDI, то есть любое применение ПП над CDI не приведет к нарушению целостности CDI. Правило 3. Только ПП может вносить изменения в CDI. Другими словами, процедуры и действия, не являющиеся ПП, не могут изменить CDI. Это обеспечивает замкнутость преобразований в пределах набора CDI. Правило 4. Субъекты могут инициировать только определенные ПП над определенными CDI. Это правило предполагает, что система безопасности должна определять и поддерживать некоторые отношения между субъектами ПП и CDI - так называемые КВМ-тройки. Каждая такая тройка определяет возможность данного субъекта применить данную ПП к данному CDI. Правило 5. КВМ - тройки должны проводить некоторую соответствующую политику разделения обязанностей субъектов. Это правило предусматривает, что компьютерная система определяет такую политику, чтобы не позволять субъектам изменять CDI без соответствующего вовлечения других субъектов. Это предотвращает субъектов от возможности наносить ущерб целостности CDI. Некоторые системы управления конфигурацией предоставляют уровень разделения обязанностей. Например, в некоторых системах разработчики ПО должны представить свои модули на просмотр менеджеру по разработке ПО перед тем, как они смогут включить их в конфигурацию. Этот подход защищает целостность конфигурации ПО. Правило 6. Некоторые специальные ПП могут превращать UDI в CDI. Это правило позволяет определенным ПП получать на вход UDI и после соответствующего повышения целостности выдавать на выходе CDI. Правило 7. Каждое применение ПП должно регистрироваться в специальном CDI, в который может производиться только добавление информации, достаточной для восстановления картины о процессе работы этого CDI.
Это правило требует ведения специального регистрационного журнала, который хранится в определенном CDI. Правило 8. Система должна распознавать субъекты, пытающиеся инициировать ПП. Это правило определяет механизмы предотвращения атак, при которых один субъект пытается выдать себя за другого. Правило 9. Система должна разрешать производить изменения в списках авторизации только специальным субъектам (например, офицерам безопасности). Это правило гарантирует, что основная защита, определяемая КВМ-тройкой, не будет обойдена злоумышленником, пытающимся изменить содержание такого списка. Основным преимуществом модели КВМ является то, что она основана на проверенных временем бизнес-методах обращения с бумажными ресурсами. Модель КВМ предоставляет исследователям методы работы с целостностью, отличные от традиционных уровне-ориентированных подходов, таких как модели БЛМ и Биба.
Пример 3.1 Исходные данные – P =10-6, T =7 дней = 1 неделя, V =10 паролей / минуту = 10*60*24*7=100800 паролей в неделю. Тогда, Условию
Элементы теории чисел Модулярная арифметика Пусть m – целое число. Тогда при делении любых целых чисел на m возможно получение ровно m остатков – 0,1,2,…,m-1. Целые числа a и b называют сравнимыми по модулю m, если их разность a-b делится без остатка на m, или, что то же самое, остатки, получаемые при делении чисел a и b на m, равны между собой. В этом случае число b называют вычетом числа a по модулю m. Если a сравнимо с b по модулю m, то это записывают как Пример 4.1 Целые числа 17 и 12 сравнимы между собой по модулю 5, то есть Существует бесконечное количество чисел, сравнимых с числом a по модулю m, но только одно из них расположено в диапазоне от 0 до m-1. Обычно, для целого числа a>0 предпочитают использовать вычеты Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Целые числа по модулю m с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности. Основные свойства сравнений: 1. Рефлексивность: 2. Симметричность: 3. Транзитивность: 4. Если 5. Если 6. Если 7. Если 8. Если 9. Если При выполнении арифметических операций по модулю, можно либо сначала приводить операнды по модулю m, а затем выполнять операции, либо сначала выполнять операции, а затем приводить результат по модулю m. В криптографии используется множество вычислений по модулю m, так как с вычислениями по модулю удобнее работать в связи с ограничением диапазона всех промежуточных величин и результата. Кроме того, задачи типа вычисления дискретных логарифмов трудны в вычислительном плане.
Для модуля m длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому такую операцию, как возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов. Возведение числа a в степень x по модулю m, то есть нахождение Пример 4.2 Пусть, например, требуется вычислить
Например,
Вычисление Пример 4.3 Пусть x=25(10)=11001(2), тогда 25=24+23+20. Тогда
Поскольку многие алгоритмы шифрования основаны на возведении в степень больших чисел в большие степени по большому модулю, целесообразно использовать рассмотренные выше алгоритмы быстрого возведения в степень.
Простые числа и их свойства Натуральное число n >1 называется простым, если оно имеет в точности два различных натуральных делителя – 1 и n, в противном случае n называется составным. Пример 4.4 Числа 2,3,7 являются простыми. Числа 4,6,8 – составными, так как их делителем является число 2. Свойства простых чисел: 1. Если p1 и p2 – простые и 2. Пусть p – простое число, а n – натуральное, тогда n делится на p или наибольший общий делитель чисел n и p равен 1. 3. Если 4. Если Известна следующая теорема: Теорема 4.1. Любое натуральное число n >1 либо просто, либо раскладывается в произведение простых чисел и притом единственным образом с точностью до порядка следования сомножителей: Задача представления числа n в канонической форме называется задачей факторизации числа n. Существенный с точки зрения криптографии факт состоит в том, что в арифметике не известно никакого эффективного алгоритма факторизации числа n. Никаких эффективных методов неизвестно даже в таком простом случае, когда необходимо найти два простых числа p и q, таких, что Известен ряд подходов, позволяющих выполнить проверку простоты целого числа n – решето Эратосфена, критерий Вильсона, тестирование на основе малой теоремы Ферма, тест Соловея-Штрассена, тест Рабина-Миллера и др. Наибольшим общим делителем целых чисел a и b, обозначаемым как НОД (a, b) или просто (a, b), - это наибольшее целое, делящее одновременно числа a и b. Если (a, b)=1, то a и b называют взаимно простыми.
Числовые функции В теории чисел и в криптографии большое значение имеют следующие числовые функции [22].
Пусть канонической формой числа n является
Пример 4.5 Для числа n =720 найдем Представим число 720 в канонической форме - Тогда
Шифрование методом замены Шифрование заменой (подстановкой) заключается в том, что символы шифруемого текста заменяются символами того же или другого алфавита в соответствие с заранее обусловленной схемой замены. Данные шифры являются наиболее древними. Принято делить шифры замены на моноалфавитные и многоалфавитные. При моноалфавитной замене каждой букве алфавита открытого текста ставится в соответствие одна и та же буква шифротекста из этого же алфавита одинаково на всем протяжении текста. Рассмотрим наиболее известные шифры моноалфавитной замены. Шифрование методом Цезаря Свое название данный шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке с Цицероном (около 50 г. до н.э). При шифрование исходного текста по данному методу каждая буква заменяется на другую букву того же алфавита путем ее смещения в используемом алфавите на число позиций, равное K. При достижении конца алфавита выполнялся циклический переход к его началу. Общая формула шифра Цезаря имеет следующий вид:
где P – символ открытого текста, С – соответствующий ему символ шифротекста, K – ключ шифрования (коэффициент сдвига), M – размер алфавита (для русского языка M =32) Для данного шифра замены можно задать фиксированную таблицу подстановок, содержащую соответствующие пары букв открытого текста и шифротекста. Пример 5.1 Таблица подстановок для символов русского текста при ключе K =3 представлена в таблице 5.1. Данной таблице соответствует формула
где P – номер шифруемой буквы русском алфавите, C – номер соответствующей буквы шифротекста в русском алфавите.
Таблица 5.1. Таблица подстановок шифра Цезаря для ключа K =3
Согласно формуле (5.2) открытый текст «БАГАЖ» будет преобразован в шифротекст «ДГЖГЙ». Дешифрование закрытого текста, зашифрованного методом Цезаря согласно (5.1), осуществляется по формуле
Простая моноалфавитная замена Шифр простой моноалфавитной замены является обобщением шифра Цезаря и выполняет шифрование по следующей схеме:
где Преобразование согласно схеме (5.4) является взаимно однозначным отображением только в том случае, если a и M взаимно простые. В этом случае для дешифрования закрытого текста выполняют обратное преобразование по формуле (5.5)
Пример 5.2 Пусть M=26, a= 3, K= 6, НОД(3,26) = 1. Тогда получаем следующую таблицу подстановок для шифра простой моноалфавитной замены (в таблице указаны коды букв русского алфавита).
Тогда открытый текст «HOME» будет преобразован в шифротекст «AWQS».
Шифрующие таблицы Трисемуса Данный шифр был предложен в 1508 году аббатом из Германии Иоганом Трисемусом [4]. Для получения данного шифра замены им было предложено использовать таблицу для записи букв алфавита и ключевого слова или фразы. В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку. При шифровании в построенной таблице находят очередную букву открытого текста и записывают в шифротекст букву, расположенную ниже ее в том же столбце. Если буква открытого текста оказывается в нижней строке таблицы, тогда для шифротекста берут самую верхнюю букву из того же столбца. Для русского алфавита шифрующая таблица может иметь размер 4х8. Пример 5.3 Выберем в качестве ключа слово ПАМЯТНИК. Шифрующая таблица с данным ключом представлена в таблице 5.1. Таблица 5.1. Шифрующая таблица Трисемуса
Тогда открытый текст «НЕРУКОТВОРНЫЙ» будет преобразован в закрытый текст «ЖУЩЫЙШЕОШЩЖТЦ». Достоинством методов моноалфавитной замены является простота шифрования и дешифрования. Основным недостатком данных методов является то, что подстановки, выполняемые в соответствие с данными методами, не маскируют частоты появления различных букв закрытого текста. Это позволяет легко атаковать данные методы шифрования путем анализа частотности символов закрытого текста. Особенности реализации данного метода криптоанализа будут рассмотрены далее. При многоалфавитной замене каждой букве алфавита открытого текста в различных ситуациях ставятся в соответствие различные буквы шифротекста в зависимости от соответствующего ей элемента ключа. В данном случае для шифрования каждого символа открытого текста применяют свой шифр моноалфавитной замены, причем смена алфавитов осуществляется последовательно и циклически, т.е. первый символ заменяется соответствующим символом первого алфавита, второй – символом второго алфавита и т. д. до тех пор, пока не будут использованы все выбранные алфавиты. После этого использование алфавитов повторяется. Многоалфавитные шифры замены предложил и ввел в практику криптографии Леон Батист Альберти. Рассмотрим ряд примеров шифров многоалфавитной замены.
Шифр Гронсфельда Данный шифр представляет собой модификацию шифра Цезаря с числовым ключом. При реализации данного шифра под буквами исходного сообщения записывают цифры числового ключа. Если ключ короче сообщения, то его запись циклически повторяют. Получение символа шифротекста осуществляют также, как это делается в шифре Цезаря, при этом смещение символа открытого текста производят на количество позиций, соответствующего цифре ключа, стоящей под ним. Пример 5.4 Пусть необходимо зашифровать исходное сообщение «НОЧЕВАЛА ТУЧКА ЗОЛОТАЯ», в качестве ключа возьмем К =193431.
Для того, чтобы зашифровать первую букву сообщения Н, необходимо сдвинуть ее в алфавите русских букв на число позиций 1, в результате чего получим букву О. Дешифрование шифротеста предполагает сдвиг его символов на необходимое число позиций в обратную сторону.
Система шифрования Вижинера Отличие системы Вижинера от шифра Гронсфельда заключается в том, что элементами ключа в данном случае могут быть не только цифры от 0 до 9, но и произвольные символы некоторого алфавита. При шифровании исходного сообщения его, как и в шифре Гронсфельда, выписывают в строку, а под ним записывают ключевое слово или фразу. Если ключ оказался короче сообщения, то его циклически повторяют. Все символы используемого алфавита пронумерованы от 0 до M, где M – размер алфавита. Преобразование символа открытого текста осуществляется по формуле
где Pi - номер символа открытого текста, Ki – номер расположенного под ним символа ключа, Сi – номер символа шифротекста. Преобразование символа закрытого текста в символ открытого осуществляется по формуле Pi=Ci -Ki (mod M)
Пример 5.6 Рассмотрим пример шифрования сообщения ПРИЛЕТАЮ ДНЕМ по методу Вижинера с помощью ключевого слова СИСТЕМА
В данном случае буквы русского алфавита пронумерованы от 0 до 31: А-0, Б-1, В-2,..., Я-31.
Шифрование методом Вернама Система шифрования Вернама является частным случаем системы шифрования Вижинера при значении модуля M =2 [13]. При шифровании открытого текста, каждый его символ представляется в двоичном виде. Ключ шифрования также представляется в двоичной форме. Шифрование исходного текста осуществляется путем сложения по модулю 2 двоичных символов открытого текста с двоичными символами ключа согласно (5.7).
Дешифрование состоит в сложении по модулю 2 символов шифротекста с той же последовательностью ключей. Общая схема системы шифрования Вернама представлена на рис. 5.2.
Рис. 5.2. Схема системы шифрования Вернама Модификация системы шифрования Вернама используется для криптографической защиты информации в архиваторе ARJ. Формула (5.7) в этом случае преобразуется в следующую:
где VALUE – фиксированное значение. Пример 5.7 Зашифруем с помощью системы Вернама открытый текст «БЛАНК» с помощью ключа «ОХ». Преобразуем открытый текст «БЛАНК» в ASCII коды: Б=193, Л=203, A=192, Н=205, К=202. В двоичном виде последовательность 193, 203, 192, 205, 202 представится в виде 11000001 11001011 11000000 11001101 11001010. Преобразуем ключ «ОХ» в ASCII коды: О=206, Х=213. В двоичном виде последовательность 206, 213 представится в виде 11001110 11010101. Подпишем циклически ключ под открытым текстом и выполним сложение по модулю 2 соответствующих битов.
G-контурная многоалфавитная замена Дан
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.019 с.) |


 к объектам
к объектам  компьютерной системы в зависимости от уровня допуска субъекта
компьютерной системы в зависимости от уровня допуска субъекта  и уровня конфиденциальности объекта
и уровня конфиденциальности объекта  на основании двух следующих правил:
на основании двух следующих правил: может читать информацию из объекта
может читать информацию из объекта  тогда и только тогда, когда
тогда и только тогда, когда  . Формально данное правило можно записать как
. Формально данное правило можно записать как  (рис. 2.2)
(рис. 2.2) . Формально данное правило можно записать как
. Формально данное правило можно записать как  (рис. 2.2).
(рис. 2.2).
 .
. удовлетворяют, например, такие пары величин A и L, как A =26, L =8 (пароль состоит из 8 малых символов английского алфавита), A =36, L =6 (пароль состоит из 6 символов, среди которых могут быть малые латинские буквы и цифры).
удовлетворяют, например, такие пары величин A и L, как A =26, L =8 (пароль состоит из 8 малых символов английского алфавита), A =36, L =6 (пароль состоит из 6 символов, среди которых могут быть малые латинские буквы и цифры).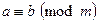 .
.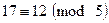 , кроме этого
, кроме этого  .
.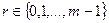 . Набор целых чисел от 0 до (m-1) называют полным набором вычетов по модулю m.
. Набор целых чисел от 0 до (m-1) называют полным набором вычетов по модулю m.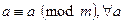 .
. .
. .
. - произвольные целое число, то
- произвольные целое число, то  .
. , то
, то  , то
, то  .
. , то
, то  .
. , то
, то  .
. .
. можно легко выполнить как ряд умножений. Особенно легко возводить в степень по модулю, если
можно легко выполнить как ряд умножений. Особенно легко возводить в степень по модулю, если  - степень двойки.
- степень двойки.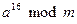 . В этом случае не следует выполнять серию умножений и одно приведение по модулю большого числа. Вместо этого выполняют три малых умножения и три малых приведения по модулю.
. В этом случае не следует выполнять серию умножений и одно приведение по модулю большого числа. Вместо этого выполняют три малых умножения и три малых приведения по модулю.

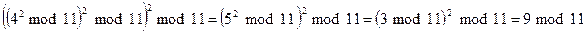

 .
. , то p1 не делится на p2.
, то p1 не делится на p2. делится на простое число
делится на простое число  , то m делится на p или n делится на p.
, то m делится на p или n делится на p. делится на простое число
делится на простое число  , которое делится на
, которое делится на  , где
, где  . Данное разложение называется канонической формой числа n.
. Данное разложение называется канонической формой числа n. .
. - определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая:
- определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая:  .
. - определяет количество всех делителей числа n.
- определяет количество всех делителей числа n. .
. - определяет сумму всех делителей числа n,
- определяет сумму всех делителей числа n, 
 - функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,
- функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,
 .
.


 ,
,
 - ключ шифрования,
- ключ шифрования,  .
.




